第二场 hdu 6050 Funny Function
Function Fx,yFx,ysatisfies:
![]()
For given integers N and M,calculate Fm,1Fm,1 modulo 1e9+7.
For given integers N and M,calculate Fm,1Fm,1 modulo 1e9+7.
InputThere is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.
OutputFor each given N and M,print the answer in a single line.
Sample Input
2 2 2 3 3
Sample Output
2 33
题目大意:按照题目所给的方式求F[m][1]?
解题思路:对于任意i>=1,当j>=3时,有通过归纳法可以得到
进而推导出
通过矩阵快速幂求解。
这个思路能够推出矩阵A、B0、B1

然后能够用快速幂模板很容易求出F[m][1]
AC代码:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <vector> 6 #include <bits/stdc++.h> 7 #define N 101000 8 #define ll long long 9 using namespace std; 10 const int SMod=1e9+7; 11 struct Matrix 12 { 13 ll m[2][2]; 14 }; 15 Matrix Mul(Matrix a,Matrix b) 16 { 17 Matrix c; 18 memset(c.m,0,sizeof(c.m)); 19 for(int i=0; i<2; i++) 20 for(int j=0; j<2; j++) 21 for(int k=0; k<2; k++) 22 c.m[i][j]+=((a.m[i][k]*b.m[k][j])%SMod+SMod)%SMod; 23 return c; 24 } 25 Matrix fastm(Matrix a,ll n) 26 { 27 Matrix res; 28 memset(res.m,0,sizeof(res.m)); 29 res.m[0][0]=res.m[1][1]=1; 30 while(n) 31 { 32 if(n&1) 33 res=Mul(res,a); 34 n>>=1; 35 a=Mul(a,a); 36 } 37 return res; 38 } 39 int main() 40 { 41 Matrix A,B0,B1; 42 ll t,n,m; 43 //freopen("1006.in","r",stdin); 44 //freopen("1006.out","w",stdout); 45 while(~scanf("%lld",&t)) 46 { 47 while(t--) 48 { 49 A.m[0][0]=0,A.m[0][1]=1; 50 A.m[1][0]=2,A.m[1][1]=1; 51 B0.m[0][0]=1,B0.m[0][1]=0; 52 B0.m[1][0]=0,B0.m[1][1]=1; 53 B1.m[0][0]=-1,B1.m[0][1]=1; 54 B1.m[1][0]=2,B1.m[1][1]=0; 55 scanf("%lld%lld",&n,&m); 56 A=fastm(A,n); 57 // for(int i=0;i<2;i++) 58 // { 59 // for(int j=0;j<2;j++) 60 // printf("%lld ",A.m[i][j]); 61 // printf("\n"); 62 // } 63 if(n%2==0) 64 { 65 for(int i=0; i<2; i++) 66 for(int j=0; j<2; j++) 67 A.m[i][j]-=B0.m[i][j]; 68 } 69 else 70 { 71 for(int i=0; i<2; i++) 72 for(int j=0; j<2; j++) 73 A.m[i][j]-=B1.m[i][j]; 74 } 75 A=fastm(A,m-1); 76 printf("%lld\n",(A.m[0][0]+A.m[0][1]+SMod)%SMod); 77 } 78 } 79 return 0; 80 }


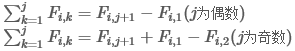
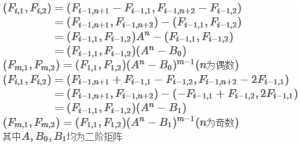


 浙公网安备 33010602011771号
浙公网安备 33010602011771号