最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

方法1：暴力法

求一个字符串的最长回文子串，我们可以将以每个字符为首的子串都遍历一遍，判断是否为回文，如果是回文，再判断最大长度的回文子串。

复杂度分析

• 时间复杂度：O(n^3)，假设 n 是输入字符串的长度，则 2n(n−1)​ 为此类子字符串(不包括字符本身是回文的一般解法)的总数。因为验证每个子字符串需要 O(n) 的时间，所以运行时间复杂度是 O(n^3)。
• 空间复杂度：O(1)。 

string longestPalindrome(string &s)
{
    int len = s.size();                  //字符串长度
    int maxlen = 1;                      //最长回文字符串长度
    int start = 0;                       //最长回文字符串起始地址
    for(int i = 0; i < len; i++)         //起始地址
    {
        for(int j = i + 1; j < len; j++) //结束地址
        {
            int tmp1 = i, tmp2 = j;
            while(tmp1 < tmp2 && s.at(tmp1) == s.at(tmp2))//判断是不是回文
            {
                tmp1++;
                tmp2--;
            }

            if(tmp1 >= tmp2 && j - i + 1 > maxlen)
            {
                maxlen = j - i + 1;
                start = i;
            }
        }
    }

    return s.substr(start, maxlen);
}

 

方法2：动态规划

为了改进暴力法，我们首先观察如何避免在验证回文时进行不必要的重复计算。考虑“ababa” 这个示例。如果我们已经知道 “bab” 是回文，那么很明显，“ababa” 一定是回文，因为它的左首字母和右尾字母是相同的。

设状态dp[j][i]表示索引j到索引i的子串是否是回文串。则转移方程为：

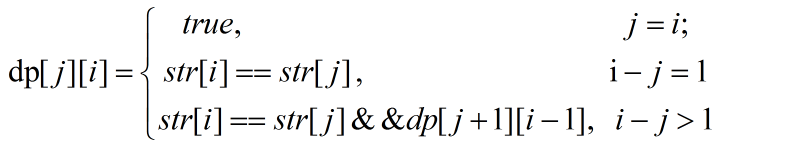
复杂度分析

• 时间复杂度：O(n^2)， 这里给出我们的运行时间复杂度为 O(n^2) 。

• 空间复杂度：O(n^2)， 该方法使用 O(n^2) 的空间来存储表。

class Solution {
public:
    string longestPalindrome(string s) {
        if(s.empty())
        {
            return "";
        }
        
        const int n = s.size();
        bool dp[n][n];
        memset(dp, 0, sizeof(dp));
        
        int maxlen = 1;
        int start = 0;
        
        for(int i = 0; i < n; ++ i)
        {
            for(int j = 0; j <= i; ++ j)
            {
                if(i - j < 2)
                {
                    dp[j][i] = (s[j] == s[i]);
                }
                else
                {
                    dp[j][i] = (s[j] == s[i] && dp[j+1][i-1]);
                }
                
                if(dp[j][i] && maxlen < (i - j + 1))
                {
                    maxlen = (i - j + 1);
                    start = j;
                }
            }
        }
        
        return s.substr(start, maxlen);
    }
};

 

方法3：中心扩展法

 

中心扩展就是把给定的字符串的每一个字母当做中心，向两边扩展，这样来找最长的子回文串。

复杂度分析

• 时间复杂度：O(n^2)， 由于围绕中心来扩展回文会耗去 O(n) 的时间，所以总的复杂度为 O(n^2)。

• 空间复杂度：O(1)。 

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.empty())
            return "";
        int left = 0, right = 0;//存回文子串的起始点和终止点位置
        for (int i = 0; i < s.size(); ++i) {
            int l = i - 1; int r = i + 1;//记录向两边扩展时的位置
            while (l >= 0) {//先向左边扩展，将与i对应的字符相同的都放进子串
                if (s[l] == s[i]) {
                    l--;
                }
                else
                    break;
            }
            while (r < s.size()) {//再向右扩展
                if (s[r] == s[i]) {
                    r++;
                }
                else
                    break;
            }
            while (l >= 0 && r < s.length()) {//中心（可能是多个相同的字符）已经确定好了，接下来是同时向两边扩展
                if (s[l] == s[r]) {
                    l--;
                    r++;
                }
                else
                    break;
            }

            if (right - left < r - l - 2) {//如果以i为中心确定的子串比之前的小则替换，记录下新的起点和终点
                left = l + 1;
                right = r - 1;
            }
        }
        return s.substr(left, right - left + 1);//返回最终的子串
    }
};