二分图

关于二分图

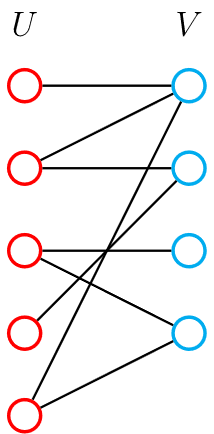
判断是否为二分图

左部和右部的点之间不存在连边，即不存在奇环；

codes

点击查看代码

#include<bits/stdc++.h>
using namespace std;

const int maxn=1e5+10;

int n,m,tot;
int to[maxn*2],nxt[maxn*2],w[maxn*2],h[maxn];
int col[maxn],x[maxn],y[maxn],z[maxn];

inline void add(int x,int y,int z)
{
	to[++tot]=y;
	nxt[tot]=h[x];
	h[x]=tot;
	w[tot]=z;
}

bool dfs(int now,int fa,int color)
{
	col[now]=color;
	for(int i=h[now];i;i=nxt[i])
	{
		if(to[i]==fa)continue;
		if(col[to[i]]==color)return false;
		if(!col[to[i]] and !dfs(to[i],now,3-color))return false;
	}
	return true;
}

inline bool judge()
{
	for(int i=1;i<=n;i++)
	{
		if(!col[i])
		{
			if(!dfs(i,0,1))return false;
		}
	}
	return true;
}

int main()
{
	ios::sync_with_stdio(false);
	
	//读入建图
    if(judge())cout <<"yes";
    else cout <<"no";
	
	return 0;
}

二分图应用（匈牙利算法）

点击查看代码

#include<bits/stdc++.h>
using namespace std;

const int maxn=3000;

int n,m,tot;
int h[maxn],to[maxn],nxt[maxn];
int match[maxn];
bool vis[maxn];

inline void add(int x,int y)
{
	to[++tot]=y;
	nxt[tot]=h[x];
	h[x]=tot;
}

bool dfs(int now)
{
	for(int i=h[now];i;i=nxt[i])
	{
		int v=to[i];
		if(vis[v])continue;
		vis[v]=true;
		if(!match[v] or dfs(match[v]))
		{
			match[v]=now;
			return true;
		}
	}
	return false;
}

inline int xyl()
{
	int ans=0;
	for(int i=1;i<=m;i++)
	{
		memset(vis,0,sizeof vis);
		if(!dfs(i))return i-1;
	}
	return m;
}

int main()
{
	ios::sync_with_stdio(false);
	
	//读入建边
	int ans=xyl();
	cout <<ans;
	
	
	return 0;
}

二分图详解

更多详解