P4168 [Violet] 蒲公英（题解）

题目#

题目描述#

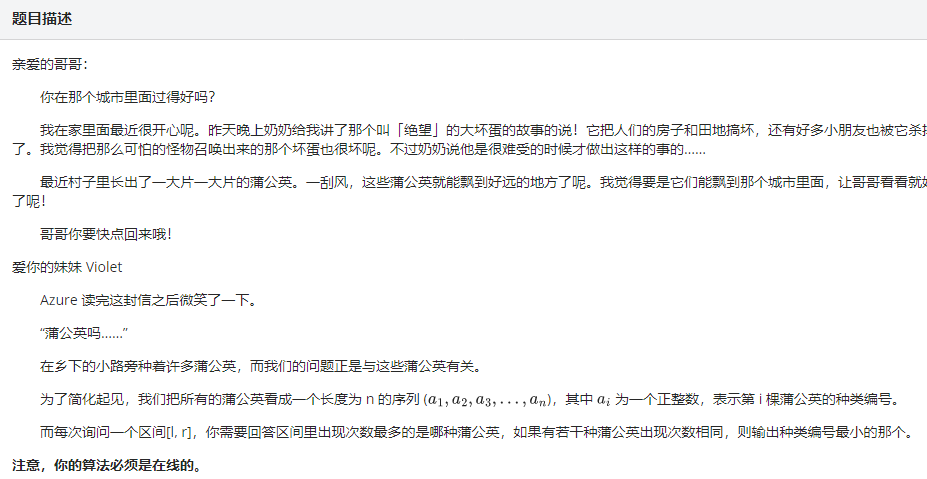
输入格式#

输出格式#

数据范围#

![]

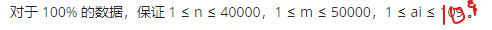
样例#

Copy
输入：
6 3 
1 2 3 2 1 2 
1 5 
3 6 
1 5 

输出：
1 
2 
1

思路#

暴力#

本题求区间内的最小众数，容易想到去用数组sum[i]表示第i种花的个数，在去便利比较，但是复杂度nm一定会T，这时候就要对暴力进行优化。

分块优化1#

如果我们将所给数列进行分块，记录sum[i][j]每一块中的每一种花的数量，在进行比较，这样在询问的时候就可以少便利中间整块的花，而只便利两边的残缺块即可，但这样仍然会T。
这时候就可以更改sum[i][j]的含义为前i个块中j这一种花的个数。从而减小整块的花的询问复杂度。

代码时间#

这个代码是可以过掉 洛谷，acwing（我只在这两个网站（除了hzoi）上交了）的。

点击查看代码

Copy
#include<bits/stdc++.h>
using namespace std;

const int maxx=4e4+10;
const int maxn=210;

int cnt,n,m,ans,res;
int belong[maxx],mark[maxx],vis[maxx];
int st[maxn],ed[maxn];
int sum[maxn][maxx];

struct floures
{
	int sp,b,id;
}a[maxx];

int read()
{
	int ans=0;bool f=0;char ch=getchar();
	while(ch<'0' || ch>'9'){if(ch=='-')f=1;ch=getchar();}
	while(ch>='0' && ch<='9'){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}
	return f?~ans+1:ans;
}

void manba_out(int x)
{
	if(x<0){manba_out('-');x=-x;}
    if(x>9)manba_out(x/10);
    putchar(x%10+'0');
}

bool cmp(floures x,floures y)
{
	return x.sp<y.sp;
}

bool cmpp(floures x,floures y)
{
	return x.id<y.id;
}

inline void lsh()
{
	sort(a+1,a+1+n,cmp);
	a[1].b=++res;
	vis[a[1].b]=a[1].sp;
	for(register int i=2;i<=n;i++)
	{
		if(a[i].sp==a[i-1].sp)a[i].b=a[i-1].b;
		else a[i].b=++res;
		vis[res]=a[i].sp;
	}
	sort(a+1,a+1+n,cmpp);
}

inline void prepare()
{
	cnt=(int)sqrt(n);
	for(register int i=1;i<=cnt;i++)
	{
		st[i]=(i-1)*cnt+1;
		ed[i]=i*cnt;
	}
	if(ed[cnt]<n)
	{
		cnt++;
		st[cnt]=ed[cnt-1]+1;
		ed[cnt]=n;
	}
	for(register int i=1;i<=cnt;i++)
	{
		for(register int j=st[i];j<=ed[i];j++)
		{
			belong[j]=i;
			sum[i][a[j].b]++;
		}
		for(register int j=1;j<=res;j++)
		{
			sum[i][j]+=sum[i-1][j];
		}
	}
}

inline int query(int l,int r)
{	
	int ans=0,cut=0;
	memset(mark,0,sizeof mark);
	if(belong[l]==belong[r])
	{
		for(register int i=l;i<=r;i++)
		{
			mark[a[i].b]++;
		}
		cut=mark[1];
		ans=vis[1];
		for(register int i=2;i<=res;i++)
		{
			if(mark[i]>cut)
			{
				cut=mark[i];
				ans=vis[i];
			}
		}
		return ans;
	}
	for(register int i=l;i<=ed[belong[l]];i++)
	{
		mark[a[i].b]++;
	}
	for(register int i=st[belong[r]];i<=r;i++)
	{
		mark[a[i].b]++;
	}
	if(belong[r]-1>belong[l])
	{
		for(register int i=1;i<=res;i++)
		{
			mark[i]+=(sum[belong[r]-1][i]-sum[belong[l]][i]);
			if(mark[i]>cut)
			{
				cut=mark[i];
				ans=vis[i];
			}
		}
	}
	else
	{
		for(register int i=1;i<=res;i++)
		{
			if(mark[i]>cut)
			{
				cut=mark[i];
				ans=vis[i];
			}
		}
	}
	return ans;
}

int main()
{
	n=read();m=read();
	for(register int i=1;i<=n;i++)
	{
		a[i].sp=read();
		a[i].id=i;
	}
	lsh();
	prepare();
	for(register int i=1;i<=m;i++)
	{
		int x,y;
		x=read();y=read();
		int l=(x+ans-1)%n+1;
		int r=(y+ans-1)%n+1;
		if(l>r)swap(l,r);
		ans=query(l,r);
		manba_out(ans);
		putchar('\n');
	}
	
	
	return 0;
}

分块优化2#

上个优化需要去便利花的种类，在极限状态下种类为n，复杂度又成了nm，所以我们可以在记录一个mode[i][j]表示第i个块和第j个块的最小众数，这样就不需要便利颜色了。

点击查看代码

Copy
#include<bits/stdc++.h>
using namespace std;

const int maxx=4e4+10;
const int maxn=210;

int cnt,n,m,man,res;
int belong[maxx],mark[maxx],vis[maxx];
int st[maxn],ed[maxn];
int sum[maxn][maxx],mode[maxn][maxn];

struct floures
{
	int sp,b,id;
}a[maxx];

int manba_in()
{
	int ans=0;bool f=0;char ch=getchar();
	while(ch<'0' || ch>'9'){if(ch=='-')f=1;ch=getchar();}
	while(ch>='0' && ch<='9'){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}
	return f?~ans+1:ans;
}

void manba_out(int x)
{
	if(x<0){manba_out('-');x=-x;}
    if(x>9)manba_out(x/10);
    putchar(x%10+'0');
}

bool cmp(floures x,floures y)
{
	return x.sp<y.sp;
}

bool cmpp(floures x,floures y)
{
	return x.id<y.id;
}

inline void memset_mark_0(int l,int r)
{
	for(register int i=l;i<=ed[belong[l]];i++)
	{
		mark[a[i].b]=0;
	}
	for(register int i=st[belong[r]];i<=r;i++)
	{
		mark[a[i].b]=0;
	}
}

inline void lsh()
{
	sort(a+1,a+1+n,cmp);
	a[1].b=++res;
	vis[a[1].b]=a[1].sp;
	for(register int i=2;i<=n;i++)
	{
		if(a[i].sp==a[i-1].sp)a[i].b=a[i-1].b;
		else a[i].b=++res;
		vis[res]=a[i].sp;
	}
	sort(a+1,a+1+n,cmpp);
}

inline void prepare()
{
	cnt=(int)sqrt(n);
	for(register int i=1;i<=cnt;i++)
	{
		st[i]=(i-1)*cnt+1;
		ed[i]=i*cnt;
	}
	if(ed[cnt]<n)
	{
		cnt++;
		st[cnt]=ed[cnt-1]+1;
		ed[cnt]=n;
	}
	for(register int i=1;i<=cnt;i++)
	{
		for(register int j=st[i];j<=ed[i];j++)
		{
			belong[j]=i;
			sum[i][a[j].b]++;
		}
		for(register int j=1;j<=res;j++)
		{
			sum[i][j]+=sum[i-1][j];
		}
	}
	for(register int i=1;i<=cnt;i++)
	{
		int op,num,opn;
		for(register int j=i;j<=cnt;j++)
		{
			op=mode[i][j-1];
			for(register int k=st[j];k<=ed[j];k++)
			{
				opn=sum[j][op]-sum[i-1][op];
				num=sum[j][a[k].b]-sum[i-1][a[k].b];
				if((num>opn)||(num==opn&&vis[op]>vis[a[k].b]))
				{
					op=a[k].b;
				}
			}	
			mode[i][j]=op;
		}
	}
}

inline int query(int l,int r)
{	
	int ans=0,cut=0,val=0;
	if(belong[l]==belong[r])
	{
		for(register int i=l;i<=r;i++)
		{
			mark[a[i].b]++;
			if((mark[a[i].b]>cut)||(mark[a[i].b]==cut&&ans>a[i].b))
			{
				cut=mark[a[i].b];
				ans=a[i].b;
			}
		}
		memset_mark_0(l,r);
		return vis[ans];
	}
	for(register int i=l;i<=ed[belong[l]];i++)
	{
		mark[a[i].b]++;
	}
	for(register int i=st[belong[r]];i<=r;i++)
	{
		mark[a[i].b]++;
	}
	ans=mode[belong[l]+1][belong[r]-1];
	for(register int i=l;i<=ed[belong[l]];i++)
	{
		cut=sum[belong[r]-1][ans]-sum[belong[l]][ans]+mark[ans];
		val=sum[belong[r]-1][a[i].b]-sum[belong[l]][a[i].b];
		if((mark[a[i].b]+val>cut)||(mark[a[i].b]+val==cut&&vis[a[i].b]<vis[ans]))
		{
			ans=a[i].b;
		}
	}
	for(register int i=st[belong[r]];i<=r;i++)
	{
		cut=sum[belong[r]-1][ans]-sum[belong[l]][ans]+mark[ans];
		val=sum[belong[r]-1][a[i].b]-sum[belong[l]][a[i].b];
		if((mark[a[i].b]+val>cut)||(mark[a[i].b]+val==cut&&vis[a[i].b]<vis[ans]))
		{
			ans=a[i].b;
		}
	}
	memset_mark_0(l,r);
	return vis[ans];
}

int main()
{
	n=manba_in();m=manba_in();
	for(register int i=1;i<=n;i++)
	{
		a[i].sp=manba_in();
		a[i].id=i;
	}
	lsh();
	prepare();
	for(register int i=1;i<=m;i++)
	{
		int x,y;
		x=manba_in();y=manba_in();
		int l=(x+man-1)%n+1;
		int r=(y+man-1)%n+1;
		if(l>r)swap(l,r);
		man=query(l,r);
		manba_out(man);
		putchar('\n');
	}
	
	
	return 0;
}