dp总结(背包,线性,区间,坐标,树形)
背包dp
- 这种dp的运行很像一个人向一个有限制的背包里放物品,而且这个人很贪心,想用最少的空间创造最大的价值
0/1背包
- 这种背包会提供可选的物品,背包的容积以及每件物品的价值,并且在选择物品是每件物品只有选一件或不选两种状态。
例题:0/1背包

输入
4 5
1 2
2 4
3 4
4 5
输出
8
二维解法代码
//状态转移方程为:f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i])
#include"bits/stdc++.h"
using namespace std;
const int maxn=1010;
const int maxw=1010;
//f[i][j]表示前i件物品占j空间的最大价值
//v[i]表示第i件物品所占的体积
//w[i]表示选第i件物品可以创造的价值
int f[maxn][maxn],v[maxn],w[maxn];
int n,m;
int main()
{
cin >>n>>m;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
//枚举每一件物品
{
for(int j=0;j<=m;j++)
//记录背包的容量
{
f[i][j]=f[i-1][j];
//若不选第i件物品,前i件物品创造的价值等于前i-1件物品创造的价值
if(j>=v[i])
//保证背包剩余的容量可以装下第i件物品
{
f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
//若选第i件物品,比较不选i和选i所创造的价值,f[i][j]为两种情况中更优的一种
}
}
}
cout <<f[n][m];
//输出前n件物品占m容量时的最大价值
return 0;
}
- 本题中背包现在的状态会存入i中,背包上一次的状态存在于i-1中,而现在的状态只与上一次的状态有关,所以可以用滚动数组将二维优化为一维
一维解法代码
//状态转移方程为:f[j]=max(f[j],f[j-v[i]]+w[i])
#include"bits/stdc++.h"
using namespace std;
const int maxn=1010;
const int maxw=1010;
////f[i][j]仍然表示前i件物品占j空间的最大价值,但i体现在第一层循环中
int f[maxw],v[maxn],w[maxn];
int n,m;
int main()
{
cin >>n>>m;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
//背包容量需要倒序保证每个物品只会被判断一次,即保证每种物品最多选一个(必须倒序)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout <<f[m];
return 0;
}
完全背包
- 在完全背包中,所提供的物品不仅有价值和所占容积,还会提供每种物品拥有的数量,也就是说,每种物品有选一件,选多件和不选三种状态,而选一件和选多件可以统一看成选k件
例题:完全背包问题
设有n种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为M,今从n种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于M,而价值的和为最大。
输入
10 4
2 1
3 3
4 5
7 9
输出
max=12
二维解法代码
//状态转移方程与0/1背包很像,只是每种物品选择的数量由一件变为k件
//状态转移方程:f[i][j]=max(f[i-1][j-k*v[i]]+k*w[i],f[i][j])
#include"bits/stdc++.h"
using namespace std;
const int maxn=3000;
int f[maxn][maxn],v[maxn],w[maxn];
int n,m;
int main()
{
cin >>m>>n;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
//枚举每种物品
{
for(int j=0;j<=m;j++)
//记录背包容积
{
for(int k=0;k*v[i]<=j;k++)
//枚举每种物品选择的数量
{
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout <<"max="<<f[n][m];
return 0;
}
- 与0/1背包相同,完全背包现在的状态i也只与上个状态i-1相关,所以也可以用滚动数组优化为一维
一维解法代码
//状态转移方程与0/1背包相似
//状态转移方程:f[j]=max(f[j-k*v[i]]+k*w[i],f[j])
//但我们可以将完全背包看成0/1背包,此时需要将每个物品看做一个选取对象,而不是一种物品,此时状态转移方程就变为0/1背包的状态转移方程
//状态转移方程为:f[j]=max(f[j],f[j-v[i]]+w[i])
#include"bits/stdc++.h"
using namespace std;
const int maxn=3000;
int f[maxn],v[maxn],w[maxn];
int n,m;
int main()
{
cin >>m>>n;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=m;j++)
//这层循环是完全背包和0/1背包不同的地方,正序遍历为了把每种物品中的每个拆开,从而使完全背包变为0/1背包(必须正序)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout <<"max="<<f[m];
return 0;
}
多重背包
- 多重背包类似于完全背包,也是以种类为单位提供每种物品的信息,但与完全背包不同的是,多重背包每件物品的数量是固定的(即k∈k[i])
例题:多重背包

输入
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出
10
转0/1背包解法代码
//通过遍历的物品的顺序已经将多重背包转化为0/1背包,所以状态转移方程和0/1相同
//状态转移方程:f[j]=max(f[j],f[j-v[i]]+w[i])
#include <bits/stdc++.h>
using namespace std;
const int maxn=110;
int n,m;
int f[maxn];
int v[maxn],w[maxn],s[maxn];
int main()
{
cin >>n>>m;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i]>>s[i];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=s[i];j++)//i,j两层循环将每种物品的每一个拆分开,形成0/1背包
{
for(int k=m;k>=v[i];k--)
{
f[k]=max(f[k],f[k-v[i]]+w[i]);
}
}
}
cout <<f[m];
return 0;
}
- 直接将多重背包转换为0/1背包的复杂度很大,容易被卡时间,所以可以用二进制拆分进行优化
二进制拆分
- 原理
任何数字都可以表示成若干个2ⁿ的和(eg:7=2º+2¹+2²),因为任何整数都可以转成二进制,二进制就是若干个“1”(2的幂数)的和,所以我们可以将物品i拆成体积为v[i]×2ⁿ,价值为w[i]×2ⁿ的若干个物品
二进制拆分解法代码
//已经通过二进制拆分将物品拆成0/1背包,所以状态转移方程与0/1背包相同
//状态转移方程为:f[j]=max(f[j],f[j-v[i]]+w[i])
#include <bits/stdc++.h>
using namespace std;
const int maxn=15000;
const int maxm=2010;
int n,m;
int f[maxm];
int v[maxn],w[maxn],s[maxn],cnt;
int main()
{
int vi,wi,si;
cin >>n>>m;
//二进制拆分
for(int i=1; i<=n; i++)
{
cin >>vi>>wi>>si;
if(si>m/vi)si=m/vi;
for(int j=1;j<=si;j<<=1)
{
v[++cnt]=j*vi;
w[cnt]=j*wi;
si-=j;
}
if(si>0)
{
v[++cnt]=si*vi;
w[cnt]=si*wi;
}
}
//0/1背包
for(int i=1;i<=cnt;i++)
{
for(int j=m;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout <<f[m];
return 0;
}
分组背包
- 分组背包中物品和0/1背包相同,都是以个位单位,但是分组背包中的物品会划分到不同的组中,并且题中会出现与组相关的限制条件
例题:分组背包
一个旅行者有一个最多能用V公斤的背包,现在有n件物品,它们的重量分别是W1,W2,...,Wn,它们的价值分别为C1,C2,...,Cn。这些物品被划分为若干组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
输入格式
第一行:三个整数,V(背包容量,V<=200),N(物品数量,N<=30)和T(最大组号,T<=10);
第2..N+1行:每行三个整数Wi,Ci,P,表示每个物品的重量,价值,所属组号。
输出格式
仅一行,一个数,表示最大总价值。
输入
10 6 3
2 1 1
3 3 1
4 8 2
6 9 2
2 8 3
3 9 3
输出
20
二维解法代码
//分组背包就是以组为单位进行0/1背包,所以状态转移方程和0/1背包相同
//状态转移方程::f[i][j]=max(f[i-1][j],f[i-1][j-v[g[i][k]]]+w[g[i][k]]
#include"bits/stdc++.h"
using namespace std;
const int maxn=2500;
int n,m,t;
int v[maxn],w[maxn];
int dp[15][maxn],g[15][maxn];
//dp[i][j]表示在背包容量为j对第i组的第k个物品的决策最大值
//g[i][j]表示第i组第j个物品的编号
int main()
{
cin >>m>>n>>t;
int x;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i]>>x;
g[x][++g[x][0]]=i;
}
//以组为单位进行0/1背包
for(int i=1;i<=t;i++)
{
//0/1背包
for(int j=0;j<=m;j++)
{
dp[i][j]=dp[i-1][j];
for(int k=1;k<=g[i][0];k++)
{
if(j>=v[g[i][k]])
{
x=g[i][k];
dp[i][j]=max(dp[i][j],dp[i-1][j-v[x]]+w[x]);
}
}
}
}
cout <<dp[t][m];
return 0;
}
- 在分组背包中,当前组i所产生的最大价值只与上一组i-1所产生的最大价值有关,所以可以用滚动数组优化
一维解法代码
//分组背包就是以组为单位进行0/1背包,所以状态转移方程和0/1背包相同
//状态转移方程为:f[j]=max(f[j],f[j-v[i]]+w[i])
#include"bits/stdc++.h"
using namespace std;
const int maxn=2500;
int n,m,t;
int v[maxn],w[maxn];
int dp[maxn],g[15][maxn];
int main()
{
cin >>m>>n>>t;
int x;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>w[i]>>x;
g[x][++g[x][0]]=i;
}
//以组为单位进行0/1背包
for(int i=1;i<=t;i++)
{
//0/1背包(与一维0/1背包相同,需要倒序遍历)
for(int j=m;j>=0;j--)
{
for(int k=1;k<=g[i][0];k++)
{
if(j>=v[g[i][k]])
{
x=g[i][k];
dp[j]=max(dp[j],dp[j-v[x]]+w[x]);
}
}
}
}
cout <<dp[m];
return 0;
}
二维费用背包
- 顾名思义,这种背包需要开二维的dp(至少目前没见过用一维的),这种背包和其他背包不同的是,它不只有体积这一个限制,还有质量的限制(当然体积和质量用别的也可以平替),所以我们在遍历时需要体找到积不超限制的同时质量也不超限制的最优方案
例题:NASA的食物计划
航天飞机的体积有限,当然如果载过重的物品,燃料会浪费很多钱,每件食品都有各自的体积、质量以及所含卡路里,在告诉你体积和质量的最大值的情况下,请输出能达到的食品方案所含卡路里的最大值,当然每个食品只能使用一次.
输入格式
第一行两个数体积最大值(<400)和质量最大值(<400)
第二行 一个数 食品总数N(<50).
第三行-第3+N行
每行三个数 体积(<400) 质量(<400) 所含卡路里(<500)
输出格式
一个数 所能达到的最大卡路里(int范围内)
输入
320 350
4
160 40 120
80 110 240
220 70 310
40 400 22
输出
550
唯一会的一种解法代码
//因为有两个条件限制,所以状态转移方程中应出现两个条件
//状态转移方程:f[j][k]=max(f[j][k],f[j-v[i]][k-m[i]]+w[i])(i为物品的编号)
#include"bits/stdc++.h"
using namespace std;
const int maxn=10000;
//f[i][j]表示在体积不超过i且质量不超过j时的最优方案
int f[maxn][maxn],v[maxn],m[maxn],w[maxn];
int n,maxt,maxm;
int main()
{
cin >>maxt>>maxm>>n;
for(int i=1;i<=n;i++)
{
cin >>v[i]>>m[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=maxt;j>=v[i];j--)
{
for(int k=maxm;k>=m[i];k--)
{
f[j][k]=max(f[j][k],f[j-v[i]][k-m[i]]+w[i]);
}
}
}
cout <<f[maxt][maxm];
return 0;
}
线性dp
- 这种dp主要运用于求所给数据中的线性关系
例题1:求最长上升序列
题目描述
设有由n个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)且b(i)<>b(j) (i<>j),若存在i1<i2<i3< … < ie 且有b(i1)<b(i2)< … <b(ie)则称为长度为e的不下降序列。程
序要求,当原数列出之后,求出最长的上升序列。
例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。例中13,16,18,19,21,22,63就是一个长度为7的不下降序列,同时也有7 ,9,16,18,
19,21,22,63长度为8的不下降序列。
输入格式
只有一行,为若干正整数(最多1000个数)
输出格式
为两行,第一行为最上升序列的长度。 第二行为该序列
样例输入
13 7 9 16 38 24 37 18 44 19 21 22 63 15
样例输出
max=8
7 9 16 18 19 21 22 63
解法代码
//状态转移方程:f[i]=max(f[j]+1,f[i])
#include"bits/stdc++.h"
using namespace std;
const int maxn=1200;
int n,ans,te;
int dp[maxn],s[maxn],pre[maxn];
//dp[i]表示前i个数的最长上升序列
//pre[i]=j表示在上升序列中第一个比编号为i小的数编号为j
void output(int x)
{
if(x==0)return;
output(pre[x]);
cout <<s[x]<<" ";
}
int main()
{
int cnt=0;
while(cin >>s[++cnt]);
for(int i=1;i<=cnt;i++)
{
dp[i]=1;//任何数自己都为长度为1的上升序列
for(int j=1;j<i;j++)
{
if(s[i]>s[j]&&dp[i]<dp[j]+1)
{
dp[i]=dp[j]+1;
pre[i]=j;//标记路径
}
}
if(ans<dp[i])
{
ans=dp[i];
te=i;
}
}
cout <<"max="<<ans<<endl;
output(te);//递归输出路径
return 0;
}
例题2:打鼹鼠
题目描述
鼹鼠是一种很喜欢挖洞的动物,但每过一定的时间,它还是喜欢把头探出到地面上来透透气的。根据这个特点阿Q编写了一个打鼹鼠的游戏:在一个nn的网格中,在某些时刻鼹鼠会在某一个网格探出头来透透气。你可以控制一个机器人来打鼹鼠,如果i时刻鼹鼠在某个网格中出现,而机器人也处于同一网格的话,那么这个鼹鼠就会被机器人打死。而机器人每一时刻只能够移动一格或停留在原地不动。机器人的移动是指从当前所处的网格移向相邻的网格,即从坐标为(i,j)的网格移向(i-1, j),(i+1, j),(i,j-1),(i,j+1)四个网格,机器人不能走出整个nn的网格。游戏开始时,你可以自由选定机器人的初始位置。现在你知道在一段时间内,鼹鼠出现的时间和地点,希望你编写一个程序使机器人在这一段时间内打死尽可能多的鼹鼠。
输入格式
第一行为n(n<=1000), m(m<=10000),其中m表示在这一段时间内出现的鼹鼠的个数,接下来的m行每行有三个数据time,x,y表示有一只鼹鼠在游戏开始后time个时刻,在第x行第y个网格里出现了一只鼹鼠。Time按递增的顺序给出。注意同一时刻可能出现多只鼹鼠,但同一时刻同一地点只可能出现一只鼹鼠。
输出格式
仅包含一个正整数,表示被打死鼹鼠的最大数目
样例输入
2 2
1 1 1
2 2 2
样例输出
1
解法代码
//本题机器人在单位时间内的运动距离有限,所以在进行状态转移前先判断机器人位置是否合适
//状态转移方程:f[i]=max(f[i],f[j]+1)
#include"bits/stdc++.h"
using namespace std;
int n,m,ans;
int f[20000+250];
//f[i]表示前i只鼹鼠可打中的最大值
struct dys
{
int t,x,y;
}d[10000+250];
int main()
{
cin >>n>>m;
for(int i=1;i<=m;i++)
{
cin >>d[i].t>>d[i].x>>d[i].y;
}
for(int i=1;i<=m;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(d[i].t-d[j].t>=abs(d[i].x-d[j].x)+abs(d[i].y-d[j].y))
f[i]=max(f[i],f[j]+1);
}
ans=max(ans,f[i]);
}
cout <<ans;
return 0;
}
区间dp
- 这种dp要求在给定的区间内,对区间的子区间进行操作(题目中给到的),并找出最终操作的最大值
例题1:石子合并
题目描述
在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出1个算法,计算出将N堆石子合并成1堆最大得分.
输入格式
数据的第1行试正整数N,1≤N≤2000,表示有N堆石子.第2行有N个数,分别表示每堆石子的个数.
输出格式
输出共1行,最大得分
样例
样例输入
4
4 4 5 9
样例输出
54
注:在一个园形操场的四周摆放N堆石子->这表示最后一堆石子可以和第一堆石子合并->要求对着n堆石子进行破环成链
点击查看代码
//状态转移方程:dp[begin][end]=max(dp[begin][end-1],dp[begin+1][end])+sum[begin~end]
#include <bits/stdc++.h>
using namespace std;
const int N = 2500+2500;
//dp[i][j]表示区间[i~j]产生的最大值
int dp[N][N];
int s[N];
int sum[N];
int n;
int main()
{
cin >>n;
for(int i=1;i<=n;i++)
{
cin >>s[i];
s[i+n]=s[i];//破环成链
}
for(int i=1;i<=n*2;i++)
{
sum[i]=sum[i-1]+s[i];//求前i堆石子的前缀和
}
for(int len=1;len<=n;len++)
{
for(int i=1;i<=2*n;i++)
{
if(i+len<2*n)
{
dp[i][i+len]=max(dp[i][i+len-1],dp[i+1][i+len])+sum[i+len]-sum[i-1];
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
ans=max(ans,dp[i][n+i-1]);
}
cout <<ans;
return 0;
}
例题2:乘积最大
这道题我单独写多题解 https://www.cnblogs.com/wang-qa/p/18008917
坐标dp
- 这个dp就很像在一个棋盘里运行,会出现位置关系
例题1:矩阵取数游戏
题目描述
帅帅经常跟同学玩一个矩阵取数游戏:对于一个给定的nm的矩阵,矩阵中的每个元素aij,均为非负整数。游戏规则如下:
1.每次取数时须从每行各取走一个元素,共n个。m次后取完矩阵所有元素;
2.每次取走的各个元素只能是该元素所在行的行首或行尾;
3.每次取数都有一个得分值,为每行取数的得分之和,每行取数的得分=被取走的元素值2^i,其中i表示第i次取数(从1开始编号);
4. 游戏结束总得分为m次取数得分之和。
帅帅想请你帮忙写一个程序,对于任意矩阵,可以求出取数后的最大得分。
输入格式
输入文件game.in包括n+1行: 第1行为两个用空格隔开的整数n和m。 第2-n+l行为n*m矩阵,其中每行有m个用单个空格隔开的非负整数。
输出格式
输出文件game.out仅包含1行,为一个整数,即输入矩阵取数后的最大得分
样例输入
2 3
1 2 3
3 4 2
样例输出
82
数据范围与提示
m,n<100
解法代码
//每次操作都会在每行的行首或行尾选数
//状态转移方程:dp[t][i][j]=max(dp[t][i+1][j]+a[k]*s[t][i],dp[t][i][j-1]+a[k]*s[t][j])(t->行数,[i~j]->区间)
#include"bits/stdc++.h"
using namespace std;
#define iint __int128//数据位数小于39位时可以用int128
const int maxn=120;
//dp[t][i][j]表示第t行剩余区间[i~j]的最优解
iint dp[maxn][maxn][maxn],a[maxn],ans;
int s[maxn][maxn];
int n,m;
//int128不能用正常输出
void print(iint x){
if(x<0){
putchar('-');
x=-x;
}
if(x>9)
{
print(x/10);
}
putchar(x%10+'0');
}
int main()
{
cin >>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin >>s[i][j];
}
}
a[0]=1;
for(int i=1;i<=110;i++)
{
a[i]=a[i-1]<<1;
}
for(int t=1;t<=n;t++)
{
for(int len=1;len<=m;len++)
{
for(int i=1;i+len-1<=m;i++)
{
int j=i+len-1;
int k=m-j+i;
dp[t][i][j]=max(dp[t][i+1][j]+a[k]*s[t][i],dp[t][i][j-1]+a[k]*s[t][j]);
}
}
}
for(int i=1;i<=n;i++)
{
ans+=dp[i][1][m];
}
print(ans);
return 0;
}
例题2:盖房子
题目描述
永恒の灵魂最近得到了面积为n*m的一大块土地(高兴ING_),他想在这块土地上建造一所房子,这个房子必须是正方形的。但是,这块土地并非十全十美,上面有很多不平坦的地方(也可以叫瑕疵)。这些瑕疵十分恶心,以至于根本不能在上面盖一砖一瓦。他希望找到一块最大的正方形无瑕疵土地来盖房子。不过,这并不是什么难题,永恒の灵魂在10分钟内就轻松解决了这个问题。现在,您也来试试吧。
输入格式
输入文件第一行为两个整数n,m(1<=n,m<=1000),接下来n行,每行m个数字,用空格隔开。0表示该块土地有瑕疵,1表示该块土地完好。
输出格式
一个整数,最大正方形的边长。
样例输入
4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1
样例输出
2
解法代码
//状态转移方程:dp[i][j]=minn(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])+1(因为短板原则所以用min)
#include"bits/stdc++.h"
using namespace std;
const int maxn=1010;
int n,m,ans;
int dp[maxn][maxn],s[maxn][maxn];
//dp[i][j]表示以点[i,j]为右下角的正方形的最大边长
int minn(int a,int b,int c)
{
a=min(a,b);
a=min(a,c);
return a;
}
int main()
{
cin >>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin >>s[i][j];
}
}
//因为点[i,j]为正方形的右下角,所以在遍历dp[i][j]前应将dp[i][j-1],dp[i-1][j],dp[i-1][j-1]都遍历完,所以按左上到右下的顺序遍历
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(s[i][j]==0)continue;
dp[i][j]=minn(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])+1;
ans=max(ans,dp[i][j]);
}
}
cout <<ans;
return 0;
}
树形dp
- 我自认为这是这五个dp里最难的一个(可能是因为我太菜了吧)
- 树形dp,顾名思义就是在树上进行dp,而树上没有环这一特性就非常dfs(不撞南墙不回头),所以一般树形dp都是用dfs解决,拓扑排序也可以,但我还没学。
- 在树形dp的题中,一般来说第一步都是建图(或建树),在建图时需要注意图的性质(有向图/无向图),之后就开始遍历树的每一个节点(一般从叶子节点开始,极个别题目从根遍历)
树形dp中的dfs
- 因为一般是从叶子节点到根节点的遍历顺序,所以先dfs(子节点),在进行本节点的动归,这里给出代码。
从子节点遍历的dfs代码
for(遍历所有的儿子节点)
{
dfs(儿子节点);
进行本节点的动归;
}
树形dp中的建图
- 基于树非常dfs的特性,建树也可以用dfs,这里给出板子代码
树形dp中的建图代码
void build(int x)
{
tot++;//tot初始值为0,且tot为全局变量
if(既没有左子树,又没有右子树)return;
else if(只有左子树)
{
son[x][1]=tot+1;
build(tot+1);
return;
}
else if(既有左子树,又有右子树)
{
son[x][1]=tot+1;
build(tot+1);
son[x][2]=tot+1;
build(tot+1);
return;
}
}
树上背包问题
- 情境:在树的结构上对节点进行选与不选的操作(即进行背包dp),这里给出代码
树上背包问题dfs代码
void dfs(int x)
{
for(i 遍历所有的儿子节点)
{
int son=i
dfs(son);
for(j 0/1背包:倒序;完全背包:正序)
{
for(k k∈[0~j-1])
{
dp[x][k]=max/min(dp[x][j],dp[son][k]+dp[x][j-k-v[root]]+w[son])
}
}
}
}
例题:二叉苹果树
题目描述
有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有1个儿子的结点) 这棵树共有N个结点(叶子点或者树枝分叉点),编号为1-N,树根编号一定是1。 我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有4个树枝的树
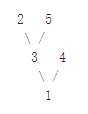
现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量,求出最多能留住多少苹果。
输入格式
第1行2个数,N和Q(1<=Q<= N,1<N<=100)。N表示树的结点数,Q表示要保留的树枝数量。接下来N-1行描述树枝的信息。每行3个整数,前两个是它连接的结点的编
号。第3个数是这根树枝上苹果的数量。每根树枝上的苹果不超过30000个。
输出格式
一个数,最多能留住的苹果的数量。
样例输入
5 2
1 3 1
1 4 10
2 3 20
3 5 20
样例输出
21
解法代码
//状态转移防方程与0/1背包相似:dp[x][k]=max/min(dp[x][j],dp[son][k]+dp[x][j-k-v[root]]+w[son])
#include"bits/stdc++.h"
using namespace std;
const int maxn=1010;
int n,q,root,tot;
int f[maxn][maxn],son[maxn][maxn],a[maxn];
int to[maxn],nxt[maxn],w[maxn],h[maxn];
//f[i][j]表示以i为树根的子树上保留j个树枝所产生的最大价值
void add(int x,int y,int z)
{
to[++tot]=y;
nxt[tot]=h[x];
h[x]=tot;
w[tot]=z;
}
void dfs(int x,int fa)
{
for(int i=h[x];i;i=nxt[i])
{
int y=to[i];
if(y==fa)continue;//存图为无向图,加入if(y==fa)continue防止死循环
dfs(y,x);
for(int j=q;j>0;j--)//0/1背包->倒序
{
for(int k=0;k<j;k++)
{
f[x][j]=max(f[x][j],f[x][j-k-1]+f[y][k]+w[i]);
}
}
}
}
int main()
{
cin >>n>>q;
for(int i=1;i<n;i++)
{
int x,y,z;
cin >>x>>y>>z;
add(x,y,z);
add(y,x,z);
}
dfs(1,0);
cout <<f[1][q];
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号