Diffie-Hellman密钥协商协议

Diffie-Hellman密钥协商协议

在进入主题之前我们先铺垫一些基础知识，或者也可以直接跳到1.3部分。

0.0 基础铺垫

定义 0.1

设m>1是整数，a为正整数，(a,m)=1,使得：

\(a^x≡1\,mod\,m\)

成立的最小正整数x，被叫做a模m的阶，记做\(ord_m(a)\)

举个例子，设m=7，计算a=2的阶：\(2^3≡1(mod\,7)\)，所以\(ord_m(a)=3\)

同理，a=3时，\(3^6≡1(mod\,7)\),所以\(ord_m(a)=6\)

需要提到的是，由于φ(m)=φ(7)=7-1=6，故理论上\(ord_m(a)\)中最大的为6（a=1,2,3,4,5,6）

定义 0.2

若\(ord_m(a)=φ(m)\),则称a为m的原根（生成元）。

因此，我们上文提到的例子里，3模7的阶刚好等于φ(7)，所以3为原根。

引入 0.3

下面我们引入群的概念，简单来说就是3可以生产群(Z/7Z)*中的任意元素（即1-6）

\(3^1≡3(mod\,7)\) \(3^2≡2(mod\,7)\) \(3^3≡6(mod\,7)\) \(3^4≡4(mod\,7)\)

\(3^5≡5(mod\,7)\) \(3^6≡1(mod\,7)\)

可以看到这是一个循环群，由此可知，3可以生成群中的元素1-6：

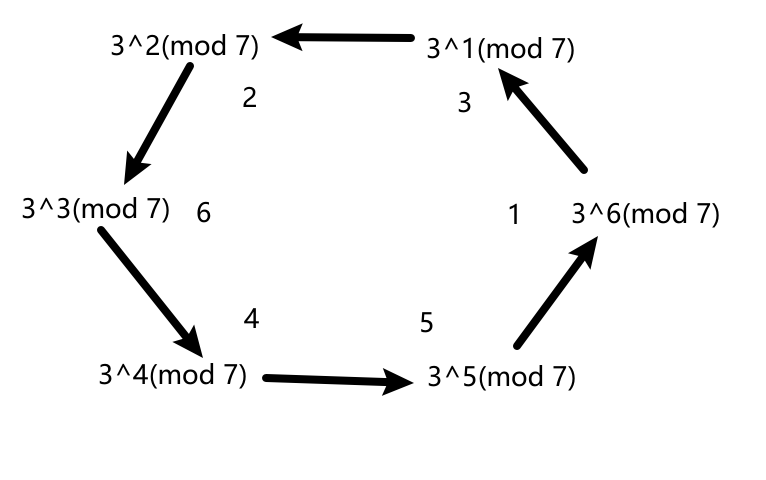
如果是2的话就不能生成所有元素：

\(2^1=2(mod\,7)\) \(2^2=4(mod\,7)\) \(2^3=1(mod\,7)\)

它就只能生成2,4,1这三个元素，因为其阶小于φ(7)，所以不能像原根3一样生成群中所有元素。

1.0 原理介绍

1.1 离散对数问题

很多密码方案的安全性都是基于求解离散对数问题的计算复杂性：

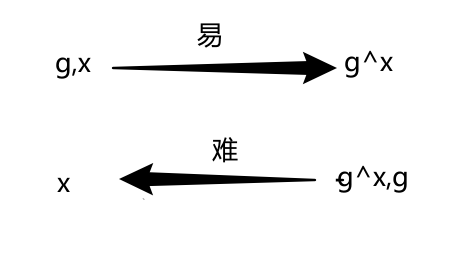
基于离散对数问题中的这种单向性，W.diffie和M.Hellman提出了Diffie-Hellman密钥协商协议。

设G是原根为g的n阶循环群（可以参考前文那个原根为3的6阶循环群理解一下这个概念），则：

1.给定整数a，计算\(g^a=y\)是容易的。

2.给定G中元素y，计算整数x(1≤x≤n)，使得\(g^x=y\)通常被认为是困难的。

1.2 离散对数问题

乘法群\(Z_p^*\)上的离散对数问题：给定一个素数p，乘法群\(Z_p^*\)上的原根g，以及\(Z_p^*\)上的随机选取的元素y，寻找整数x（2≤x≤p-2）使得\(y=g^x\,mod\,p\)。这个整数x记做\(log_gy\)，称为离散对数。

通过上文的基础铺垫部分，我们知道这个\(Z_p^*\)中的个数为p-1。

1.3 Diffie-Hellman密钥协商协议

Diffie-Hellman密钥协商协议是两轮协议，即共有两个消息在信道中传递。

每个通信方发送一个消息，并接受一个消息。

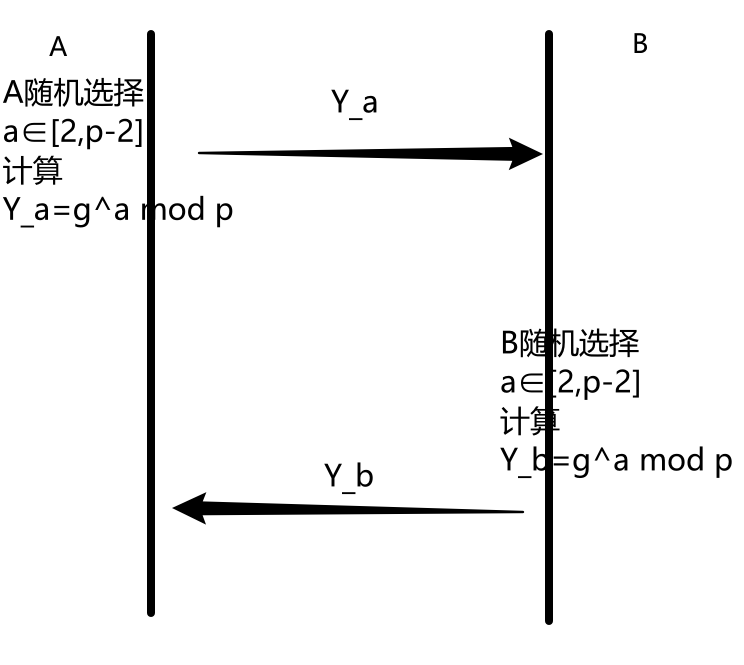
（上图B那边把a改成b，复制过去忘记改了）

1.首先A选择a∈[2,p-2]，计算\(Y_a=g^a\,mod\,p\)，并将\(Y_a\)发给B。

1.然后B选择b∈[2,p-2]，计算\(Y_b=g^b\,mod\,p\)，并将\(Y_b\)发给A。

协议交互完成后，A方以\((Y_b)^a\,mod\,p\)为密钥，B方以\((Y_a)^b\,mod\,p\)为密钥。

A方和B方之间的后续通信可以用这个密钥进行加密。

2.0 深入探讨

2.1 为什么A方和B方可以用这种方式公开地协商出一个秘密的密钥，这样为什么是可靠的？

A方计算的\((Y_b)^a\,mod\,p\)等于B方计算的\((Y_a)^b\,mod\,p\)。

这是因为

\((Y_b)^a\,mod\,p\) = \((g^b\, mod\,p)^a\,mod\,p\) = \((g^b)^a\,mod\,p\)

\((Y_a)^b\,mod\,p\) = \((g^a\, mod\,p)^a\,mod\,p\) = \((g^a)^b\,mod\,p\)

由于求解离散对数问题的困难性，攻击者就算知道了\(Y_a\)也不能求出a，即使知道了\(Y_b\)也不能求出b，既没有a也没有b，就求不出\((Y_b)^a\,mod\,p\)或者\((Y_a)^b\,mod\,p\)，也就是求不出最终的这个密钥了。

2.2 明明乘法群\(Z_p^*\)中的总个数为p-1，为什么不是a∈[1,p-1],而是a∈[2,p-2]？

如果a=1，那\(Y_a=g^a\,mod\,p\)就直接等于g了，g本身又是公开的，那就相当于直接告诉了攻击者a=1。

如果a=p-1，那那\(Y_a=g^a\,mod\,p\)就直接等于1了，也相当于直接告诉了攻击者a=p-1。

综上，不适合取1或者p-1。