纳新赛wp crypto
basic_crypto
这题原型是[UTCTF2020]basic_crypto,当时觉得非常有意思所以拿来出题了。
题目:
1010100 110000 1110110 1110110 1110110 1001001 1111000 1110101 1011010 1011000 1101000 110000 1001001 1000111 111001 1110101 1011010 1010011 1000010 110011 1100001 1010111 1111000 1110011 1001001 1000111 1001010 1101100 1001001 1000111 1000101 1100111 1100010 1000111 1101100 110000 1100100 1000111 1111000 1101100 1001001 1000111 1101000 1101000 1100011 1101101 1010001 1110011 1011001 1101110 1010110 110000 1001001 1001000 1100100 1101100 1001001 1000111 1110100 1110101 1100010 110011 1100011 1100111 1100100 1000111 1101000 1101000 1100100 1000011 1000010 110000 1100001 1000111 1010101 1100111 1011010 1101101 1111000 1101000 1011010 1111001 1000010 1110000 1100011 1111001 1000010 1101110 1100010 110010 1101100 1110101 1011010 1111001 1000010 110000 1100010 1111001 1000010 1101001 1011010 1010011 1000010 1110110 1011010 1101001 1000010 110000 1100001 1000111 1010101 1100111 1011010 1101101 111001 1111001 1100010 1010111 1000110 110000 1001001 1101101 1011010 1110011 1011001 1010111 1100100 110111 1010111 1000110 1101000 1011001 1100110 1010011 1001001 1110100 1001001 1001000 1100100 1101111 1100001 1010111 1001110 1101111 1001001 1000111 110001 1101100 1011001 1010111 110101 1111010 1001001 1001000 1010010 1101111 1011001 1011000 1010001 1100111 1100001 1010111 1011001 1100111 1100101 1010111 111001 110001 1001001 1001000 1001110 1101100 1011010 1010011 1000010 110000 1100001 1000111 1000110 110000 1001001 1001000 1000010 1101000 1100100 1001000 1010010 1101100 1100011 1101101 110100 1110011 1001001 1001000 1101100 1110110 1100100 1010011 1000010 1110010 1100010 1101101 111001 110011 1001001 1001000 1100100 1101111 1011001 1011000 1010001 1100111 1100100 1000111 1101000 1101100 1001001 1000111 1001110 1110110 1100011 1101110 1001010 1101100 1100011 110011 1000010 1110110 1100010 1101101 1010010 1101100 1100010 1101101 1001110 1101100 1100011 1111001 1000010 1101101 1100010 110011 1001001 1100111 1100100 1010011 1110111 1100111 1100100 1000011 1110111 1100111 1011010 1101001 1110111 1100111 1100010 1000011 1000010 1101000 1001100 1000011 1000010 1101000 1100010 1101101 1010001 1100111 1011010 1111001 1000010 1101000 1100011 1101101 1010101 1110101 1001001 1001000 1101100 1110110 1100100 1010011 1000010 1101010 1011001 1010111 110100 1100111 1100011 1001000 1001010 1110110 1011001 1101101 1000110 1101001 1100010 1001000 1101011 1100111 1100100 110010 111001 1111001 1100001 1111001 1000010 1110110 1100100 1011000 1010001 1100111 1100100 1000111 1101000 1101100 1001001 1001000 1001010 1101100 1100010 1010111 1000110 1110000 1100010 1101101 1101100 1110101 1011010 1111001 1000010 1101010 1100001 1000111 1000110 1111001 1011001 1010111 1001110 110000 1011010 1011000 1001010 1111010 1001001 1000111 1001010 110101 1001001 1001000 1001010 1101100 1100011 1000111 1111000 1101000 1011001 110010 1101100 1110101 1011010 1111001 1000010 110000 1100001 1000111 1010110 1110100 1001001 1000111 1000110 1110101 1011010 1000011 1000010 1110000 1100010 1101101 1011010 1101100 1100011 1101110 1001010 1110000 1100010 1101101 1100011 1100111 1011001 110010 111001 1110100 1100010 1010111 111001 1110101 1001001 1001000 1100100 1110110 1100011 1101101 1010010 1111010 1001001 1000111 1101100 1110101 1001001 1001000 1010010 1101111 1011010 1010011 1000010 1101100 1100010 1101101 1100100 1110011 1100001 1011000 1001110 1101111 1001001 1000111 1111000 1101000 1100010 1101101 1100100 110001 1011001 1010111 1100100 1101100 1001100 1101001 1000010 1101000 1100010 1101101 111001 110000 1100001 1000111 1010110 1111001 1001001 1000111 1100100 1111001 1011010 1010111 1000110 110000 1001001 1000111 110001 1101100 1100100 1000111 1101000 1110110 1011010 1000011 1000010 1110000 1100011 1111001 1000010 110000 1100010 1111001 1000010 110001 1100011 110010 1010101 1100111 1011010 1101110 1001010 1101100 1100011 1011000 1010110 1101100 1100010 1101101 1001110 110101 1001001 1000111 1000110 1110101 1011001 1010111 1111000 110101 1100011 110010 1101100 1111010 1001111 1101001 1000010 110011 1011010 1010011 1000010 1110010 1100010 1101101 111001 110011 1001001 1001000 1010010 1101111 1011001 1011000 1010001 1100111 1001010 110010 1010101 1101110 1001001 1001000 1001110 1101111 1100010 110011 1100100 1111010 1001001 1001000 1010110 1110111 1001001 1000111 110001 1110110 1100011 110011 1010001 1100111 1100010 110010 1011010 110000 1011010 1010111 110100 1100111 1100001 1010111 110100 1100111 1100100 1000111 1101000 1101100 1001001 1000111 1000110 1110011 1100011 1000111 1101000 1101000 1011001 1101101 1010110 110000 1001100 1000011 1000010 1111010 1100010 1111001 1000010 110000 1100001 1000111 1000110 110000 1001010 110011 1001101 1100111 1100011 1001000 1001010 1110110 1011001 1101101 1000110 1101001 1100010 1001000 1101011 1100111 1100100 1000111 1101000 1101100 1001001 1000111 110001 1110110 1100011 110011 1010001 1100111 1011001 110010 111001 1110100 1100010 1010111 111001 1110101 1001001 1000111 1001110 1101111 1011001 1011000 1001010 1101000 1011001 110011 1010010 1101100 1100011 1101001 1000010 1110000 1100010 1101001 1000010 110000 1100001 1000111 1010101 1100111 1100100 1000111 1010110 110100 1100100 1000011 1110111 1100111 1011010 1101101 111001 1110011 1100010 1000111 111001 110011 1011010 1010111 1010001 1100111 1011001 1101110 1101011 1100111 1001010 110011 1010001 1101110 1001100 1000011 1000010 1101000 1100010 1101101 1010001 1100111 1100011 110010 111000 1100111 1100010 110010 110100 1110101 1001001 1000111 111001 1110101 1011001 110010 1010101 1100111 1100101 1010111 111001 110001 1001001 1000111 1110100 1110101 1100010 110011 1100011 1100111 1011001 1010011 1000010 1101101 1011010 1011000 1100011 1100111 1011001 110010 1101000 1101000 1100011 1101101 1000110 1101010 1100100 1000111 1010110 1111001 1100011 1111001 1110111 1100111 1100101 1010111 111001 110001 1001001 1000111 1001110 1101000 1100010 1101001 1000010 1110000 1100010 1101101 1011010 1101100 1100011 1101001 1000010 110000 1100001 1000111 1010101 1100111 1100011 1101101 1010110 1111010 1100100 1000011 1000010 1110110 1011010 1101001 1000010 110000 1100001 1000111 1010101 1100111 1100100 110010 111001 1111001 1011010 1001000 1001101 1100111 1011001 1101101 1000110 1111010 1011010 1010111 1010001 1100111 1100010 110010 110100 1100111 1011001 110010 111001 1110100 1100010 1010111 111001 1110101 1001001 1001000 1100100 1110110 1100011 1101101 1010010 1111010 1001001 1001000 1010010 1101111 1011001 1011000 1010001 1100111 1100011 110010 1101000 1110110 1100100 1111001 1000010 110001 1100011 1000011 1000010 1110000 1100010 1101001 1000010 110000 1100001 1000111 1010101 1100111 1011010 1010111 110101 1101110 1100010 1000111 1101100 1111010 1100001 1000011 1000010 1110011 1011001 1010111 110101 1101110 1100100 1010111 1000110 1101110 1011010 1010011 110100 1001011 1100101 1000111 1110000 1110000 1011001 1101101 110001 110010 1100010 110011 1000010 1101110 1100100 1101101 111001 1101011 1100001 1101101 1101100 1110101 1001001 1010011 1000010 1101010 1100101 1101101 110001 110110 1001001 1000111 1010010 1110101 1001001 1001000 1011001 1100111 1011001 1010111 1100100 110010 1011001 1101001 1000010 1101000 1100001 1101101 110000 1100111 1100100 1101101 1100100 1101110 1001001 1001000 1010010 1110001 1100011 1000111 110000 1100111 1100101 1101101 1000110 1101000 1100001 1101101 110001 1110110 1100010 1101010 1101111 1100111 1011001 1010111 1100100 110010 1011001 1101110 1110100 1000100 1100101 1101101 1100100 1101110 1001101 1000110 111001 1011001 1100010 1011000 1010010 1110010 1100010 1111010 1000001 1101000 1100110 1010011 110100 1100111 1011001 110010 1110000 1110010 1100101 1101001 1000010 110000 1100001 1101110 1000001 1100111 1100101 1101101 1101100 1101100 1100001 1101110 1010010 110110 1100101 1010011 1000010 1110110 1011001 110011 1101111 1100111 1100101 1000111 1001110 110010 1011010 110010 1100100 110110 1100001 1010111 1001010 110110 1001001 1010001 111101 111101
解析:
打开就是二进制编码,试试直接二进制转字符。
YES, you are right. Uh-oh, looks like we have another block of text, with some sort of special encoding. Can you figure out what this encoding is?
T0vvvIxuZXh0IG9uZSB3aWxsIGJlIGEgbGl0dGxlIGhhcmQsYnV0IHdlIGtub3cgdGhhdCB0aGUgZmxhZyBpcyBnb2luZyB0byBiZSBvZiB0aGUgZm9ybWF0ImZsYWd7WFhYfSItIHdoaWNoIG1lYW5zIHRoYXQgaWYgeW91IHNlZSB0aGF0IHBhdHRlcm4sIHlvdSBrbm93IHdoYXQgdGhlIGNvcnJlc3BvbmRlbmNlcyBmb3IgdSwgdCwgZiwgbCBhLCBhbmQgZyBhcmUuIHlvdSBjYW4gcHJvYmFibHkgd29yayBvdXQgdGhlIHJlbWFpbmluZyBjaGFyYWN0ZXJzIGJ5IHJlcGxhY2luZyB0aGVtIGFuZCBpbmZlcnJpbmcgY29tbW9uIHdvcmRzIGluIHRoZSBlbmdsaXNoIGxhbmd1YWdlLiBhbm90aGVyIGdyZWF0IG1ldGhvZCBpcyB0byB1c2UgZnJlcXVlbmN5IGFuYWx5c2lzOiB3ZSBrbm93IHRoYXQgJ2UnIHNob3dzIHVwIG1vc3Qgb2Z0ZW4gaW4gdGhlIGFscGhhYmV0LCBzbyB0aGF0J3MgcHJvYmFibHkgdGhlIG1vc3QgY29tbW9uIGNoYXJhY3RlciBpbiB0aGUgdGV4dCwgZm9sbG93ZWQgYnkgJ3QnLCBhbmQgc28gb24uIG9uY2UgeW91IGtub3cgYSBmZXcgY2hhcmFjdGVycywgeW91IGNhbiBpbmZlciB0aGUgcmVzdCBvZiB0aGUgd29yZHMgYmFzZWQgb24gY29tbW9uIHdvcmRzIHRoYXQgc2hvdyB1cCBpbiB0aGUgZW5nbGlzaCBsYW5ndWFnZS4KeGppYm12b3Bndm9kamluISBjem16IGRuIHYgYWd2YiBham0gdmdnIHRqcG0gemFham1vbjogYWd2YntDemdnMF9YbXRrbzAhfS4gY2preiB0anAgemllanR6eSBvY3ogeGN2Z2d6aWJ6IQ==
好像是base系列,试试base64:
OK,next one will be a little hard,but we know that the flag is going to be of the format"flag{XXX}"- which means that if you see that pattern, you know what the correspondences for u, t, f, l a, and g are. you can probably work out the remaining characters by replacing them and inferring common words in the english language. another great method is to use frequency analysis: we know that 'e' shows up most often in the alphabet, so that's probably the most common character in the text, followed by 't', and so on. once you know a few characters, you can infer the rest of the words based on common words that show up in the english language.
xjibmvopgvodjin! czmz dn v agvb ajm vgg tjpm zaajmon: agvb{Czgg0_Xmtko0!}. cjkz tjp ziejtzy ocz xcvggzibz!
这提示非常贴心了,总结起来实际上就是考虑使用词频分析。
首先我们知道这个比赛的flag长什么样:flag{XXXXXXXXXXXXX}
因为是替换加密,所以我们看花括号就能在密文中找到对应的文本,即:agvb{Czgg0_Xmtko0!}
也就是flag=agvb
(实际上这里用的是凯撒加密,偏移量为5
那么我们就可以拿这个对应关系来进行词频分析:
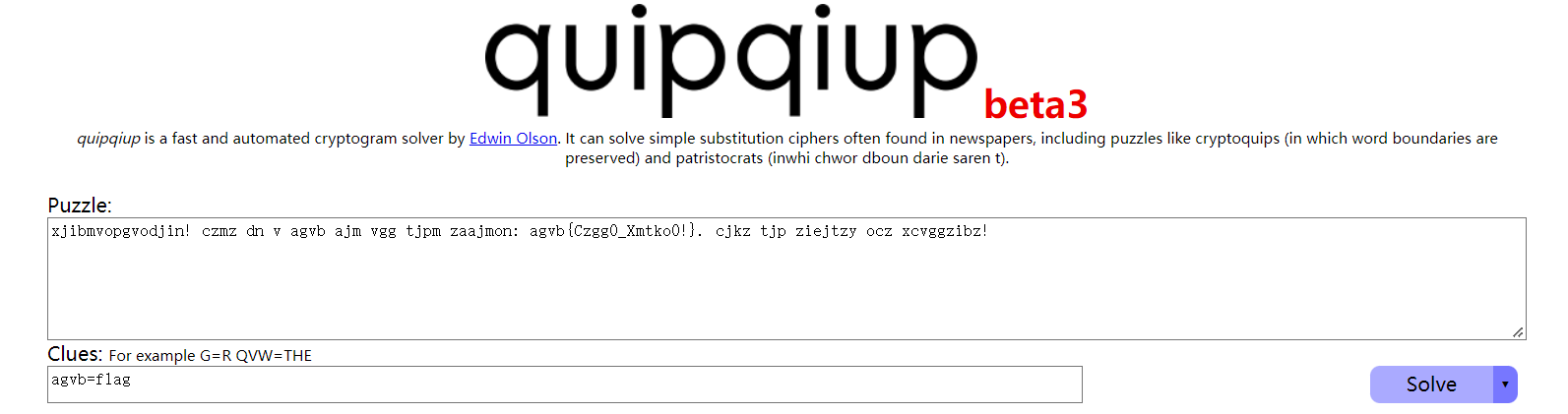
可以看到第一个即为所求:

congratulations! here is a flag for all your efforts: flag{Hell0_Crypt0!}. hope you enjoyed the challenge!
flag{Hell0_Crypt0!}
boom
本题的原型是2020网鼎杯青龙组的boom,感觉对新人比较友好所以就出了这道题。解题方法不唯一,wp仅供参考。

task1
如果新人不了解这种加密方式,可以去搜索引擎找一下。
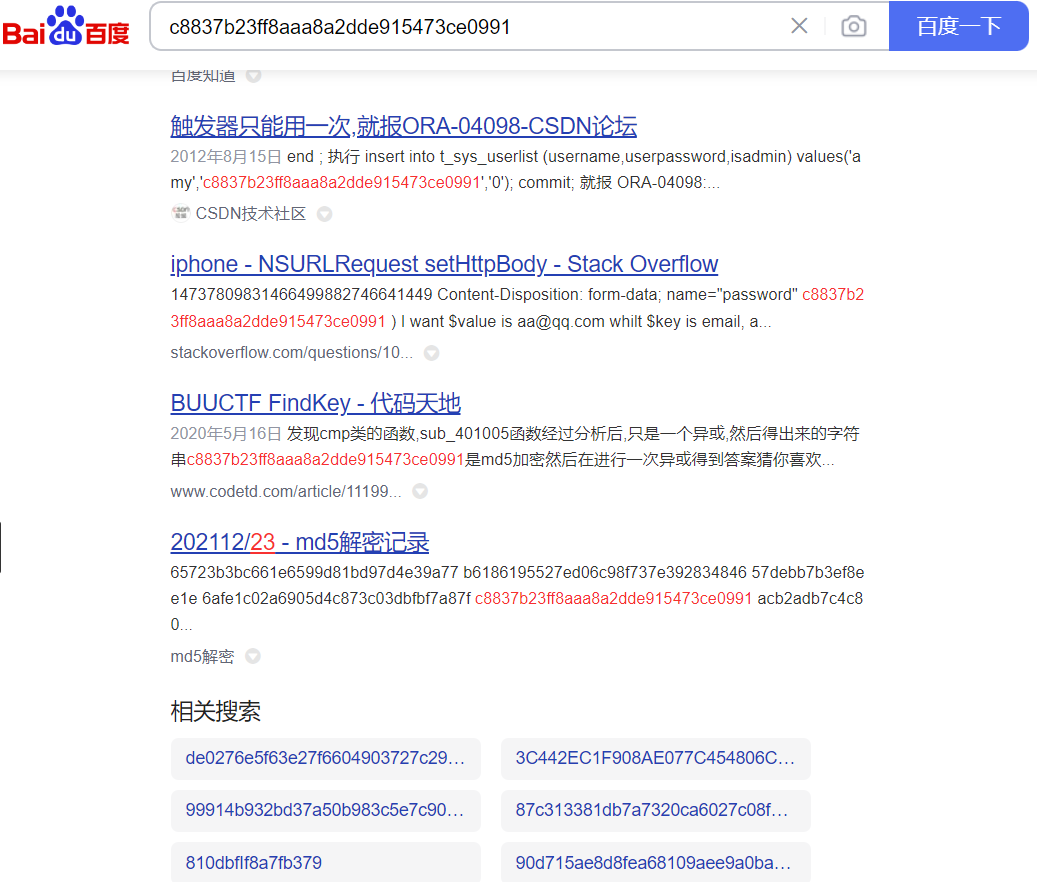
好像是md5加密,去查一下:https://www.cmd5.com/

得到:123321
输入进入下一题。
task2
可见本题需要我们解三元一次方程组。
喜报:有笔和草稿纸就能算出来!(
如果不想动笔,那不妨找找有没有在线方程求解?有的。

如果有matlab,那也可以用matlab来解方程:
syms x y z
q1=5*x-3*y+6*z==3309
q2=4*x+y-9*z==-4055
q3=2*x+8*y+5*z==3718
s=solve([q1,q2,q3],[x,y,z])

task3

是求解一元n次方程。(这可不兴拿笔算啊网友.jpg
再次尝试用在线网页解一下:
可以看到得到两个解。
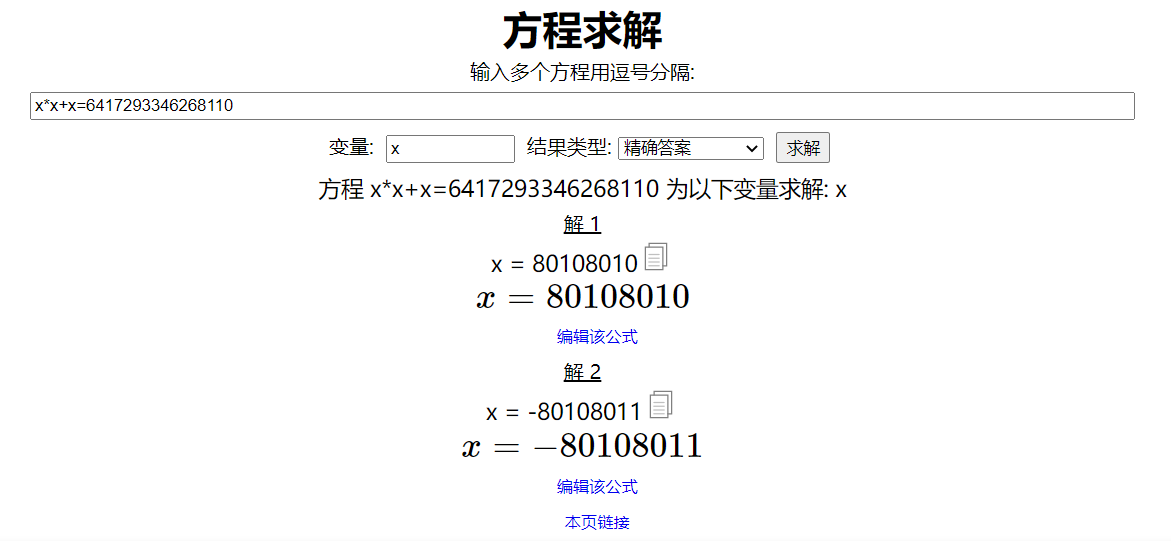
或者用matlab也可以解出:
syms x
q1=x*x+x==6417293346268110
s=solve(q1,x)

输入两解之中的任意一个解均可得到flag:

flag最后用base64加了一个密,直接转码就好:
flag{boomboomboom}
happy_ezmath
题目:
import libnum
from gmpy2 import powmod,invert,bit_length, next_prime
from secret import flag
#生成随机素数
p=libnum.generate_prime(1024)
q= next_prime(p)
e=65537
m= "flag{XXXXXXX}"
#字符串转数字
m=libnum.s2n(m)
n=p*q
phi_n=(p-1)*(q-1)
#求逆元
d=invert(e, (p-1)*(q-1))
c=pow(m,e,n)
print ("p+q=",p+q)
print ("(p+1024)*(q+1024)=",(p+1024)*(q+1024))
print ("e=",e)
print ("c=",c)
"""
Here's something for you.
p+q= 219223076311523501884304700038455762296899816974888948217004527787930877060313504497388089353341324705585325694637746358740577807120122877971299527330031129698906576598576252061554831264870000539283358012885198759131376782999938416605219761092579853328632032920645591128836645191218062394514534723716331259020
(p+1024)*(q+1024)= 12014689296872014188946259288408893749191589050238906879391904364659275201873070110579654073383396930676629081451560633069628765298632770735215486735970388804886204733085461088545719945581792410272350938500463667423654219015971587570752021846727958994511462173074900178608500876606467923865455486860346114988289402813734108787548923155669457069456131392401862913080511822686921415954179942019013762404114083254782576790936723988994231509691438970201207127691754026796499959482609500253700743306555116563598427995089859779616949688975659815627980761525858155917795434782520547110796243314223874269214650977817793067075
e= 65537
c= 8934349832062835876649016580310177315842514470594938143179273759338444576152046442761868548064534074815361761228796684262279183784621909922785373857559227140160514892741609485616942304602169623470729259140525854566022887930188634125502380822881340775020492707614401659534298319904047876928626580455556856972801506907743705626933652528565421410957794121040539639508855367711543312793880452263427685597293599896868291480923974900863658732758893499656378978989678114509648070150509204012379693036376543398310245068898356126707603583166201493068207408033030754235019071004414523449831256943021894972579549736309123153700
"""
题目给了e和c,但是没有给我们n,而是给了p+q以及(p+1024)*(q+1024)的值。
此时距离解题还需要得到n,根据定义我们知道:n=pq
所以我们接下来要做的就是从题目的已知解出pq。
\((p+1024)*(q+1024)=pq+1024p+1024q+1024*1024\)
嗯,所以:
\(n=pq=(p+1024)*(q+1024)-1024(p+q)-1024*1024\)
由此就能巧妙把n解出来了。
X=589969210495053562429957596347911701922
Y=86934482296048119190666062003494801193034127564137873545493232718639905920221
e=65537
c=8465449490631395190081015881703671542815957363708269929627413352194838803941
n=Y-1024*X-1024*1024
print(n)
n=12014689296872014188946259288408893749191589050238906879391904364659275201873070110579654073383396930676629081451560633069628765298632770735215486735970388804886204733085461088545719945581792410272350938500463667423654219015971587570752021846727958994511462173074900178608500876606467923865455486860346114763804972670734042858020910316290756477430718810115579938867875367845703306193151336693610264582597584735409065481884452638642557018685611927590491141739877215116165522540527389221553528079674564337439822800646330429087123897038721211882945402724088347398593724041435231182071567506927982286331093892294582782019
去查一下能不能分解出来:

欸,出题人这数据是随机出的,查不到啊(
但是因为题目说p是q的下一个质数,所以我们可以考虑暴力破解出来。
这里用的是yafu来分解,很快就出来了:

由此得到p,q的值:
p = 109611538155761750942152350019227881148449908487444474108502263893965438530156752248694044676670662352792662847318873179370288903560061438985649763665015564849453288299288126030777415632435000269641679006442599379565688391499969208302609880546289926664316016460322795564418322595609031197257267361858165629751
q = 109611538155761750942152350019227881148449908487444474108502263893965438530156752248694044676670662352792662847318873179370288903560061438985649763665015564849453288299288126030777415632435000269641679006442599379565688391499969208302609880546289926664316016460322795564418322595609031197257267361858165629269
之后就可以一把梭了。
import gmpy2
import binascii
e = 65537
c = 8934349832062835876649016580310177315842514470594938143179273759338444576152046442761868548064534074815361761228796684262279183784621909922785373857559227140160514892741609485616942304602169623470729259140525854566022887930188634125502380822881340775020492707614401659534298319904047876928626580455556856972801506907743705626933652528565421410957794121040539639508855367711543312793880452263427685597293599896868291480923974900863658732758893499656378978989678114509648070150509204012379693036376543398310245068898356126707603583166201493068207408033030754235019071004414523449831256943021894972579549736309123153700
X=219223076311523501884304700038455762296899816974888948217004527787930877060313504497388089353341324705585325694637746358740577807120122877971299527330031129698906576598576252061554831264870000539283358012885198759131376782999938416605219761092579853328632032920645591128836645191218062394514534723716331259020
Y=12014689296872014188946259288408893749191589050238906879391904364659275201873070110579654073383396930676629081451560633069628765298632770735215486735970388804886204733085461088545719945581792410272350938500463667423654219015971587570752021846727958994511462173074900178608500876606467923865455486860346114988289402813734108787548923155669457069456131392401862913080511822686921415954179942019013762404114083254782576790936723988994231509691438970201207127691754026796499959482609500253700743306555116563598427995089859779616949688975659815627980761525858155917795434782520547110796243314223874269214650977817793067075
n=Y-1024*X-1024*1024
print(n)
p = 109611538155761750942152350019227881148449908487444474108502263893965438530156752248694044676670662352792662847318873179370288903560061438985649763665015564849453288299288126030777415632435000269641679006442599379565688391499969208302609880546289926664316016460322795564418322595609031197257267361858165629751
q = 109611538155761750942152350019227881148449908487444474108502263893965438530156752248694044676670662352792662847318873179370288903560061438985649763665015564849453288299288126030777415632435000269641679006442599379565688391499969208302609880546289926664316016460322795564418322595609031197257267361858165629269
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = gmpy2.powmod(c,d,n)
print(binascii.unhexlify(hex(m)[2:]))
b'flag{OMEDEDO}'
恭喜恭喜。
不要爆破
本题原型来自nepctf的中学数学,当时因为没见过这种类型的题目所以没有做出来,看懂之后觉得很有意思所以放上来了。
思路分析部分与[nepctf2022]中学数学基本一致,这两篇题解只要看懂一篇就行。
题目:
from gmpy2 import *
from Crypto.Util.number import *
import libnum
from secret import flag
p=getPrime(1024)
e=65537
q=next_prime(p+(p>>100))
n=p*q
c=pow(libnum.s2n(flag),e,n)
print("n=",n)
print("c=",c)
'''
n= 15151139247958638521161578224183604125753666891843567610384261458651341723486885639327322141683430422408573179533367021925465575428670732742673335683566624711230878146516101433516556919879407050576454026155181016285301103442899309883017455912765575437461183324068217349100790019734323604740797692513581430252323555952442575358080764729350927539281276709182726045978190129019514041919402241815444805689033444952961665487282091234880344154753485590840067725415434536910144335968595341903563053900681918393556204778256248678537209952473071680623378621528697420351989127054044789541654409093645240306605753174845789869199
c= 13685386147439012795756570417270183138477965278979014263745468121989996553179966471647896675865751824403406298539906570309924629919438728755218540058016146365931948151821648688098014511088433919408897868716999030785475785611507693771986733147718959840591259886564231342949138811426178144634950873511447606539696876334147778298501806157127826707469025238306487720605333482477965173362710648425027287385661967066088187227400854332446243062606055946876523198407413825277800625725263261384893436876659844700142129214924350948435616968346478290748092685396120912332319248137858388099660396587265555128866522258901876170035
tips:
p>>100=(1/2^100)p
'''
这题关键就是把p和q分解出来,那我们就来优雅一下,缩小范围再爆破。
其中q=next_prime(p+(p>>100))指的是:\(q=[p+\frac{1}{2^{100}}p]+r\)
即:\(q=[(1+\frac{1}{2^{100}})p]+r\)
其中这个r是个为了凑到满足q为素数的最小整数。
则n为:\(n=p*q=[(1+\frac{1}{2^{100}})p^2]+rp\)
凑个平方。
得:\(\color {blue}{[(1+\frac{1}{2^{100}})n]}\color {black}{=[(1+\frac{1}{2^{100}})p]^2+(1+\frac{1}{2^{100}})rp}>\color {red} {[(1+\frac{1}{2^{100}})p]^2}\)
因为
\([(1+\frac{1}{2^{100}})n]=[(1+\frac{1}{2^{100}})p]^2+(1+\frac{1}{2^{100}})rp\) ------1式
\(q^2=[(1+\frac{1}{2^{100}})p+r]^2=[(1+\frac{1}{2^{100}})p]^2+[(1+\frac{1}{2^{100}})rp]+[(1+\frac{1}{2^{100}})rp]+r^2\) ------2式
显然2式大于1式。
因此,经过比较我们可以得到:
\([(1+\frac{1}{2^{100}})p]^2<[(1+\frac{1}{2^{100}})n]<[(1+\frac{1}{2^{100}})p+r]^2\)
这样一来,我们就可以通过开方进而缩小范围解出q:
\((1+\frac{1}{2^{100}})p<\sqrt{(1+\frac{1}{2^{100}})n}<(1+\frac{1}{2^{100}})p+r=q\)
由此,\(\sqrt{(1+\frac{1}{2^{100}})n}\)的下一位质数即为q:
q = next_prime(iroot((n + (n >> 100)), 2)[0])
但注意到next_prime算法的本质逻辑即是通过不断枚举奇数判断是否为素数,而这里n的分解保证了其必为素数,再判断素数的话属于是多此一举(浪费计算资源),所以我们可以根据素数分布公式或next_prime的方案向下枚举,得到唯一分解即可。
脚本:
from gmpy2 import *
n= 15151139247958638521161578224183604125753666891843567610384261458651341723486885639327322141683430422408573179533367021925465575428670732742673335683566624711230878146516101433516556919879407050576454026155181016285301103442899309883017455912765575437461183324068217349100790019734323604740797692513581430252323555952442575358080764729350927539281276709182726045978190129019514041919402241815444805689033444952961665487282091234880344154753485590840067725415434536910144335968595341903563053900681918393556204778256248678537209952473071680623378621528697420351989127054044789541654409093645240306605753174845789869199
c= 13685386147439012795756570417270183138477965278979014263745468121989996553179966471647896675865751824403406298539906570309924629919438728755218540058016146365931948151821648688098014511088433919408897868716999030785475785611507693771986733147718959840591259886564231342949138811426178144634950873511447606539696876334147778298501806157127826707469025238306487720605333482477965173362710648425027287385661967066088187227400854332446243062606055946876523198407413825277800625725263261384893436876659844700142129214924350948435616968346478290748092685396120912332319248137858388099660396587265555128866522258901876170035
e=65537
q = next_prime(iroot((n + (n >> 100)), 2)[0])
print("q=",q)
p=n//q
d = invert(e,(p-1)*(q-1))
print("d=",d)
m = powmod(c,d,n)
print(long_to_bytes(m))
b'flag{CUST_148ccdcc393758d14_CTF}'



 浙公网安备 33010602011771号
浙公网安备 33010602011771号