[GKCTF2021]random
[GKCTF2021]random
本题出现了MT19937伪随机数生成算法。
题目
task.py
import random
from hashlib import md5
def get_mask():
file = open("random.txt","w")
for i in range(104): #各取104个
file.write(str(random.getrandbits(32))+"\n")
file.write(str(random.getrandbits(64))+"\n")
file.write(str(random.getrandbits(96))+"\n")
file.close()
get_mask()
flag = md5(str(random.getrandbits(32)).encode()).hexdigest()
print(flag)
random.txt
分析
感觉task.py没给啥,突破点在于这个random.getrandits()
去查一下得到:
random.getrandbits(k)
生成一个k比特长的随机整数
那也就意味着生成了32/64/96比特长的随机整数,32、64/96都是32的整数倍。
这会不会也是突破口呢?
看了wp,提到了一个算法:Mersenne Twister 梅森旋转算法
MT19937算法
产生随机数的速度快、周期长,可达到\(2^{19937-1}\)
可以产生32位整数序列,在$1\le k \le 623 $的维度之间都可以均等分布。
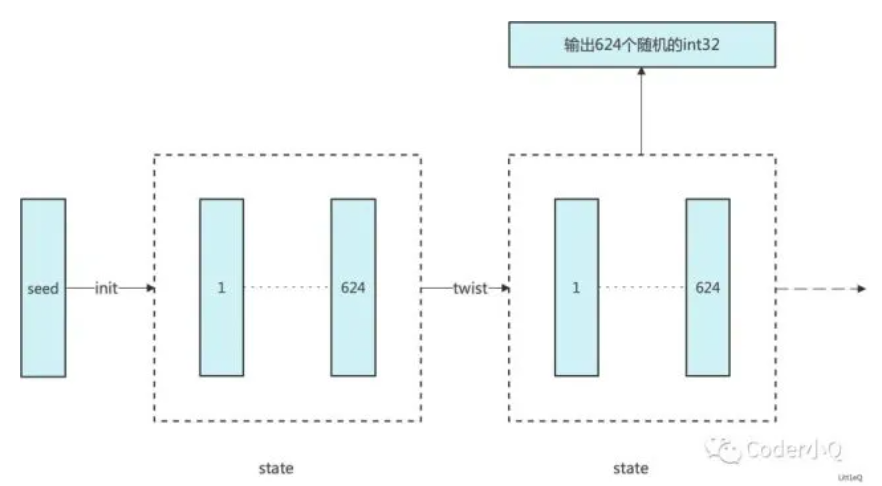
如上图所示,mt19937的随机数生成器结构首先需要一个uint32的种子,然后生成一个具有624个uint32数组的状态数组。生成状态数组之后,进行一次旋转,最终可以输出624个随机的uint32。然后重复执行旋转操作。
步骤
1.利用seed初始化624的状态
2.对状态进行旋转
3.根据状态提取伪随机数
代码实现
32位的MT19937的python代码如下:
def _int32(x):
return int(0xFFFFFFFF & x)
class MT19937:
# 根据seed初始化624的state
def __init__(self, seed):
self.mt = [0] * 624
self.mt[0] = seed
self.mti = 0
for i in range(1, 624):
self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)
# 提取伪随机数
def extract_number(self):
if self.mti == 0:
self.twist()
y = self.mt[self.mti]
y = y ^ y >> 11
y = y ^ y << 7 & 2636928640
y = y ^ y << 15 & 4022730752
y = y ^ y >> 18
self.mti = (self.mti + 1) % 624
return _int32(y)
# 对状态进行旋转
def twist(self):
for i in range(0, 624):
y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]
if y % 2 != 0:
self.mt[i] = self.mt[i] ^ 0x9908b0df
python中内置的Random类就是采用了MT19937算法,getrandbits(32)方法可以获得一个32位随机数
整个获取伪随机数的过程的重点就是这个self.mt[]也就是state块的状态。
在本题中,在random.txt中总共获取了312个随机数。其中有104个32位的,104个64位的,104个96位的。
解法1
因为本题随机数都是由32位整数序列产生,所以我们可以得知:
104个32位的需要产生104个随机数
104个64位的需要产生208个随机数
104个96位的需要产生312个随机数
所以总共需要产生624个随机数。
而这个数字刚刚好对应了624个state块的个数,理论上来讲,我们可以将624个state块的状态推出来,然后就可以推出下面产生的随机数,也就是flag了。
from random import Random
def invert_right(m,l,val=''):
length = 32
mx = 0xffffffff
if val == '':
val = mx
i,res = 0,0
while i*l<length:
mask = (mx<<(length-l)&mx)>>i*l
tmp = m & mask
m = m^tmp>>l&val
res += tmp
i += 1
return res
def invert_left(m,l,val):
length = 32
mx = 0xffffffff
i,res = 0,0
while i*l < length:
mask = (mx>>(length-l)&mx)<<i*l
tmp = m & mask
m ^= tmp<<l&val
res |= tmp
i += 1
return res
def invert_temper(m):
m = invert_right(m,18)
m = invert_left(m,15,4022730752)
m = invert_left(m,7,2636928640)
m = invert_right(m,11)
return m
def clone_mt(record):
state = [invert_temper(i) for i in record]
gen = Random()
gen.setstate((3,tuple(state+[0]),None))
return gen
f = open("random.txt",'r').readlines()
prng = []
j=0
for i in f:
i = i.strip('\n')
print(int(i).bit_length())
if(j%3==0):
prng.append(int(i))
elif(j%3==1):#将生成两次随机数的两个随机数分离出来
prng.append(int(i)& (2 ** 32 - 1))
prng.append(int(i)>> 32)
else:#将生成三次随机数的三个随机数分离出来
prng.append(int(i)& (2 ** 32 - 1))
prng.append(int(i)& (2 ** 64 - 1) >> 32)
prng.append(int(i)>>64)
j+=1
g = clone_mt(prng[:624])
for i in range(624):
g.getrandbits(32)#产生前624个随机数,让state状态到生成flag前
key = g.getrandbits(32)
print(key)
from hashlib import md5
flag = md5(str(key).encode()).hexdigest()
print(flag)
#14c71fec812b754b2061a35a4f6d8421
解法2
使用基于梅森算法的randcrack库。
randcrack一把梭:
from hashlib import md5
from randcrack import RandCrack
with open(r'random.txt', 'r') as f:
l = f.readlines()
l = [int(i.strip()) for i in l]
t = []
for i in range(len(l)):
if i % 3 == 0:
t.append(l[i])
elif i % 3 == 1:
t.append(l[i] & (2 ** 32 - 1))
t.append(l[i] >> 32)
else:
t.append(l[i] & (2 ** 32 - 1))
t.append(l[i] & (2 ** 64 - 1) >> 32)
t.append(l[i] >> 64)
rc = RandCrack()
for i in t:
rc.submit(i)
flag = rc.predict_getrandbits(32)#在给出的随机数数量多时,predict_getrandbits()可以预测下一个随机数
print('GKCTF{'+md5(str(flag).encode()).hexdigest()+'}')
GKCTF{14c71fec812b754b2061a35a4f6d8421}
总结
有师傅的文章提到:近年来MT19937在各大CTF赛事中出现的频率越来越高。
那下次再做几道加深印象。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号