[网鼎杯2020]you_raise_me_up

[网鼎杯2020]you_raise_me_up

目录

• [网鼎杯2020]you_raise_me_up
  • • • 题目
      • 分析
    • 解法一：sage
      • discrete_log()使用示例
      • 补充
    • 解法二：python
      • discrete_log()使用示例
      • 总结

题目

#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
import random

n = 2 ** 512
m = random.randint(2, n-1) | 1		#返回2到n-1之间的任意整数
c = pow(m, bytes_to_long(flag), n)
print 'm = ' + str(m)
print 'c = ' + str(c)

# m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
# c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499

分析

首先我们可以得到：$$c=m^{flag}mod,n$$

想要求出flag就要清楚：这是一道求离散对数的问题。

首先我们需要知道什么是离散对数：

\[a^x≡b(mod\,m) \]

已知a，b，m，求解x

可见这是一道非常标准的离散对数问题求解。

已知：$$c=m^{flag}mod,n$$ 和c,m,n的值。

求离散对数：

\[flag=log_{m\,mod\,n}(c\,mod\,n) \]

因为c是余数，所以：$$flag=log_{m,mod,n}c$$

解法一：sage

sage已经不陌生了，毕竟上次做一道羊城杯的题目用到了。

sage中的discrete_log()可以帮我们计算集散对数：

discrete_log()使用示例

由此编写脚本：

m=391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
n=2**512
c=6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499
flag= discrete_log((mod(c,n)), (mod(m,n)))
print(flag)

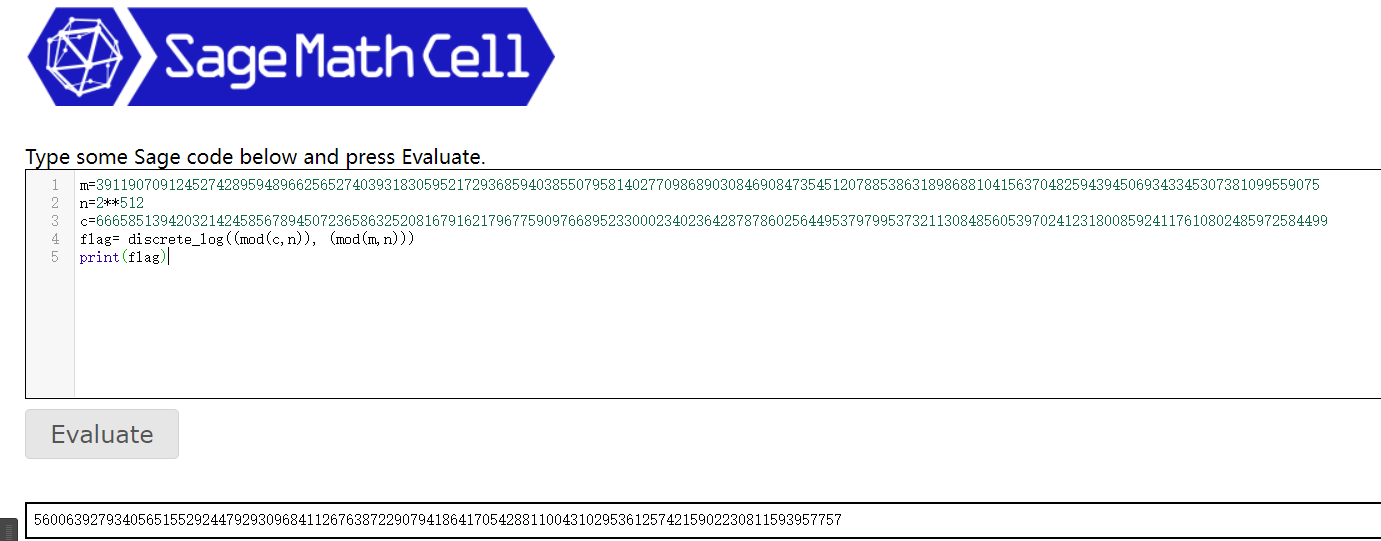
得到flag值之后再进行一个转：

from Crypto.Util.number import *

flag=56006392793405651552924479293096841126763872290794186417054288110043102953612574215902230811593957757
print(long_to_bytes(flag))

#b'flag{5f95ca93-1594-762d-ed0b-a9139692cb4a}'

补充

sage中求解离散对数有四个比较常用的函数：

(1)discrete_log：通用的求离散对数的方法：discrete_log(a,base,ord,operation)

(2)discrete_log_rho：求离散对数的Pollard-Rho算法：discrete_log_rho(a,base,ord,operation)

(3)discrete_log_lambda：求离散对数的Pollard-kangaroo算法（也称为lambda算法）：discrete_log_lambda(a,base,bounds,operation)

(4)bsgs：小步大步法：bsgs(base,a,bounds,operation)

sage使用技巧：https://blog.csdn.net/qq_39642801/article/details/104158699?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-4

在线运行sage脚本：https://sagecell.sagemath.org/

解法二：python

求解离散对数问题可以用到python的sympy库中的discrete_log()函数。

discrete_log()使用示例

from sympy.ntheory import discrete_log
discrete_log(41, 15, 7)

写脚本：

from Crypto.Util.number import *
from sympy.ntheory import discrete_log
n = 2**512
m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499
flag= discrete_log(n,c,m)
print(long_to_bytes(flag))

#b'flag{5f95ca93-1594-762d-ed0b-a9139692cb4a}'

总结

考查离散对数的概念以及求解离散对数。

https://www.bilibili.com/video/BV1ma4y1i7C7/?spm_id_from=333.788.recommend_more_video.2&vd_source=51c65e82dd2de4e2578bb3b9a956f0be