Hoyan-Sigcomm20阅读笔记

Accuracy, Scalability, Coverage – A Practical Configuration Verifier on a Global WAN

论文链接

背景

• 阿里WAN涉及的路由技术：Static/BGP/IS-IS+ACL；

• 配置验证面临的挑战：

  1. 控制平面仿真的正确性，特别是面向VSBs的模拟
  2. 基于模拟的方法进行大规模的枚举验证存在可扩展性问题【Batfish】
  3. 基于模拟的方法不能检查由于路由达到时序而产生的问题
  4. 基于逻辑表达式约束求解的方式在大规模网络中是不可行的【Minesweeper】
  5. 基于图优化的方式来减小求解范围不适用于WAN网络【ARC】

• 实际网络面临的问题：

  1. 历史累积更新多，故障产生的风险大
  2. 配置更改产生的故障代价太大

• 研究现状

  网络仿真：run the real control plane software in emulated environments and generate corresponding FIBs for validation purposes.

  数据平面验证：Data plane verification systems focus on modeling FIB snapshots to logical formulas and then checking reachability properties via solvers.

  控制平面验证：Configuration verification (or control plane verification) systems aim to comprehensively verify the logics encoded by the configurations of diverse routing protocols.

  • Simulation-based verification， 不能解决路由时序和大规模枚举验证产生的可扩展性问题

  • Formula-based，对于大规模网络，难以编码求解

  • Graph-based verification：不能编码复杂的路由协议【BGP】和路由时序问题

目的

1. audit the current configuration snapshot for hidden errors
2. check correctness and inconspicuous ambiguities of new configurations in an update

指标要求

• Mandatory： 验证时间不能超过24小时+满足常见的路由协议+正确性
• Preferred：解决k-failure和route updates racing
• Optional：支持general route inputs case

方法

准确性：与实际结果对比，不断迭代修正模型

可扩展性：Hoyan offers a globally simulation-based & locally formal-modeling-based solution to simultaneously take advantage of the scalability of simulation-based solutions and the ability to handle uncertainties of formal-modeling based solutions.

控制平面模型

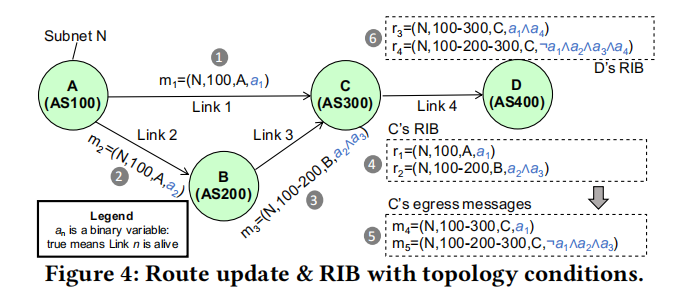
在BGP路由传播过程中,用四元组\((Subnet, AS Path, Nexthop, TopoCond)\)来表示路由宣告,前三个属性的含义和变化过程与常规的路由学习一致,因此\(routingPolicy\)和\(routingSelection\)其实只涉及到这三个属性. 最后一个属性\(TopoCond\)是一个逻辑表达式,用来记录路由更新到达当前节点所需要满足的链路状态,由一系列的\(a_i\)表示,如果\(a_i\)为true,表示\(Link_i\)能够传播此路由更新; 使用这种表达方式能够记录所有链路状态下的路由更新情况, 方便处理\(K\_failure\)和\(route\ update\ racing\)问题;

路由可达性计算过程

解决数据包\(K\_failure\)可达问题

由于保留了带有所有\(TopoCond\)的Rib, 对于某个节点所有的转发规则\(r_i\) 和这些规则里的链路状态\(R(r_i)\), 只需要找出令逻辑表达式\(R(r_1) \or ... \or R(r_n)\)值为false时. 表达式中\(a_i\)为false个数最少的情况.

解决\(route\ update\ racing\)问题

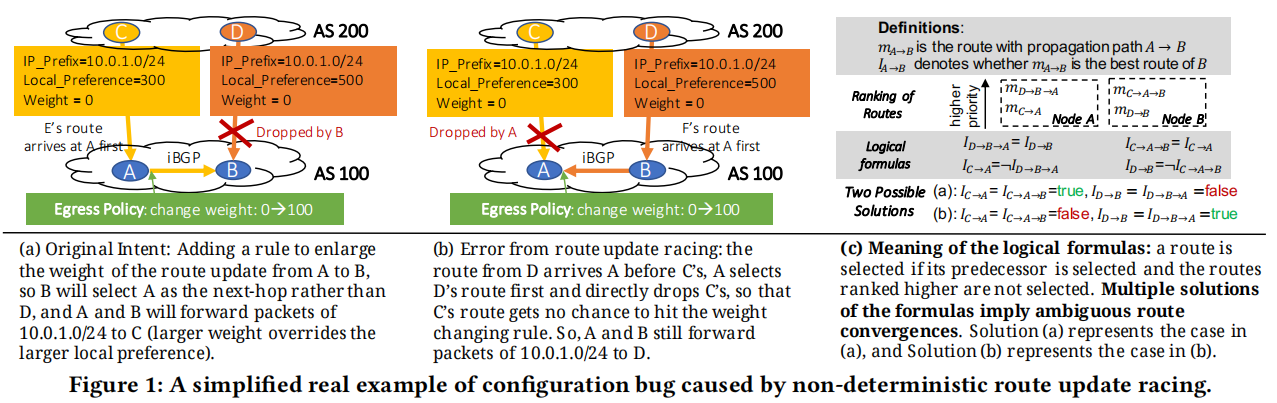
在上图这个例子中, 由于最后保留了不同链路状态下的Rib, 可以用一组公式对路由选择过程的逻辑关系进行编码。如果我们能找到多个公式的解决方案，这意味着路线收敛性不明确. 这个求解空间不会过于庞大, 原因如下:

In practice, since we have ingress and egress policies to filter routes, the actual number of potential propagation paths for a single IP prefix is moderate.

数据平面模型

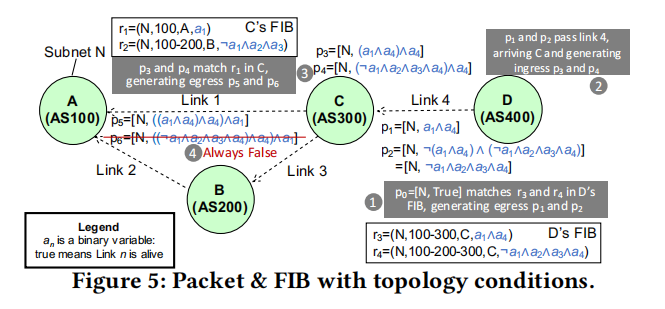
数据包转发基于Fib, ACL和Topo, Fib从Rib中继承\(TopoCond\)信息, 数据包根据子网匹配到不同\(TopoCond\)状态的转发规则\(r_i\),得到\(E(p,S)^i\). 然后结合Nexthop确定转发所经过的链路, 将数据包转发给下一跳, 记经过的链路为\(a_l\), 下一跳收到的数据包状态可以表示为\(I(p,D) = E(p, S)\and a_l\). 然后依次向下迭代. 最后目的节点会收到一系列带有\(TopoCond\)的数据包.

解决数据包\(K\_failure\)可达问题

在分组传播过程之后，可以有多个具有不同拓扑条件的数据包到达目标子网的网关。可以结合所有拓扑条件，检查是否存在小于k次故障的故障情况，从而消除了数据包的可达性。