参数估计

利用样本对总体进行统计推断的一类问题是参数估计，即假定已知总体的分布，通 常是，估计有关的参数，如。

参数估计分点估计和区间估计两种。

 

点估计

 

点估计是用样本统计量确定总体参数的一个数值。

评价估计优劣的标准有无偏性、 小方差性、有效性等，估计的方法有矩法、极大似然法等。

常用的是对总体均值 μ 和方差 σ² （或标准差 σ ）作点估计。当从一个样本按照式

、

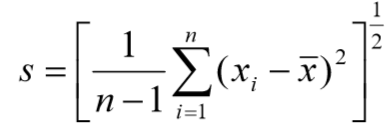
算出样本均值 x 和方差 s ² 后，对μ 和 σ² （或σ ）一个自然、合理的点估计显然是（在字母上加^表示它的估计值）

 

 

 区间估计

 

 

点估计虽然给出了待估参数的一个数值，却没有告诉我们这个估计值的精度和可信 程度。

一般地，总体的待估参数记作 θ （如 μ  , σ²），由样本算出的 θ 的估计量记作 θ ˆ ， 人们常希望给出一个区间

使得θ 以一定的概率落在此区间内。若有 

则 称为 θ 的置信区间，

分别称为置信下限和置信上限，

α −1 称为置信概率或置信水平， α 称为显著性水平。

 

给出的置信水平为α −1 的置信区间，称为 θ 的区间估计。

置信区间越小， 估计的精度越高；置信水平越大，估计的可信程度越高。

但是这两个指标显然是矛盾的， 通常是在一定的置信水平下使置信区间尽量小。

通俗地说，区间估计给出了点估计的误 差范围。