k近邻算法 ---- KNN

一、定义

给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入实例分类到这个类中。

二、k近邻模型

模型有3个要素——距离度量方法、k值的选择和分类决策规则。

1.

距离度量

 

对n维实数向量空间Rn，经常用Lp距离或曼哈顿Minkowski距离。

Lp距离：

当p=2时，称为欧氏距离。

当p=1时，称为曼哈顿距离。

当p=∞，它是各个坐标距离的最大值，叫做切比雪夫距离。

2.

k值的选择

 

k较小，容易被噪声影响，发生过拟合。

k较大，较远的训练实例也会对预测起作用，容易发生错误。

3.

分类决策规则

 

k近邻的分类决策规则是最为常见的简单多数规则，

也就是在最近的K个点中，目标归为标签数目最多的一类。

三、kd树

定义：

是一种分割K维数据空间的数据结构

kd树的构造：

1. 构造根节点，使根节点对应用于K维空间中包含所有实例点的超矩形区域。
2. 通过下面的递归，不断切分K维空间，生成子节点：
1) 在超矩形区域上选择一个坐标轴和该坐标上的一个切分点，确定一个超平面。
2)以经过该点且垂直于该坐标轴做一个超平面，该超平面将当前的超矩形区域切分成左右两个子区域，实例被分到两个子区域。
3.该过程直到子区域内无实例时终止（终止时的节点为子节点）。
在此过程中将实例集合保存在相应的节点上。

 

选取维度的顺序：

1-顺序采样，从第1维，第2维，第n维一直到分割完毕。

2-最大方差所在的维度。

3-使用维度主次优先级为顺序

 

选取分割点的度量标准：

所在维度的中位数作为切分点，也可以使用中值作为切分点

 

kd树构造算法：

输入：k维空间数据集T = x1,x2,…,xNx1,x2,…,xN，其中，xi=(x(1)i,x(2)i,…,x(k)i)，i=1,2,…,Nxi=(xi(1),xi(2),…,xi(k))，i=1,2,…,N
输出：kd树

 

构造根节点（根节点对应于包含T的K维空间的超矩形区域）
选择x(1)x(1)为坐标轴，以T中所有实例的x(1)x(1)坐标的中位数为切分点，这样，经过该切分点且垂直与x(1)x(1)的超平面就将超矩形区域切分成2个子区域。保存这个切分点为根节点。

重复如下步骤：
对深度为j的节点选择x(l)x(l)为切分的坐标轴，l=j(modk)+1l=j(modk)+1 ,以该节点区域中所有实例的x(l)x(l)坐标的中位数为切分点，将该节点对应的超平面切分成两个子区域。切分由通过切分点并与坐标轴x(l)x(l)垂直的超平面实现。保存这个切分点为一般节点。

直到两个子区域没有实例存在时停止。

 

四、kd树的检索

以查询（2.1,3.1）为例：

 

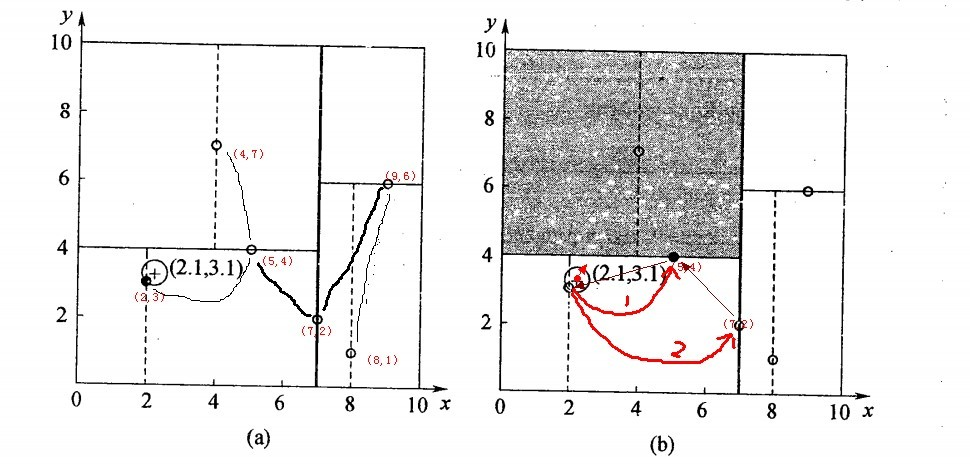
二叉树搜索：先从（7,2）点开始进行二叉查找，然后到达（5,4），最后到达（2,3），此时搜索路径中的节点为<(7,2)，(5,4)，(2,3)>，首先以（2,3）作为当前最近邻点，计算其到查询点（2.1,3.1）的距离为0.1414，

回溯查找：在得到（2,3）为查询点的最近点之后，回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如下图所示。发现该圆并不和超平面y = 4交割，因此不用进入（5,4）节点右子空间中(图中灰色区域)去搜索；

最后，再回溯到（7,2），以（2.1,3.1）为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入（7,2）右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点（2,3），最近距离为0.1414。

 

算法描述：

（1）在kd树中找出包含目标点x的叶结点：从根结点出发，递归的向下访问kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子节点，直到子节点为叶结点为止。
（2）以此叶节点为“当前最近点”。
（3）递归的向上回退，在每个结点进行以下操作：
（a） 如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”。
（b） 当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的另一子结点对应的区域是否有更近的点。
具体的，检查另一子结点对应的区域是否与以目标点为球心，以目标点与“当前最近点”间的距离为半径的超球体相交。
如果相交，可能在另一个子结点对应的区域内存在距离目标点更近的点，移动到另一个子结点，接着，递归地进行最近邻搜索。
如果不相交，向上回退。
（4）当回退到根结点时，搜索结束，最后的“当前最近点”即为x的最近邻点。