卡尔曼滤波器--连续变量
一、问题
状态变量和证据变量都是连续型的时候
比如说跟踪一只飞行的小鸟
它的状态用这六个变量来描述
就是x y z的坐标 以及x y z方向的速度
都是连续变量
用卡尔曼滤波来处理连续变量
二、
用高斯分布来模拟它的先验概率密度
(卡尔曼滤波假设状态的先验分布是高斯分布)
用线性高斯分布来模拟它的转换模型和传感器模型
可以得出任何时候的状态分布都是一个高斯分布
t时刻的状态分布:用均值为μt
协方差为σt的一个高斯分布来表示
三、预测步骤
根据1~t时刻的证据去预测t+1时刻的状态分布

![]()
把σ变成了一个积分号,把t时刻的所有状态可能乘以转换模型
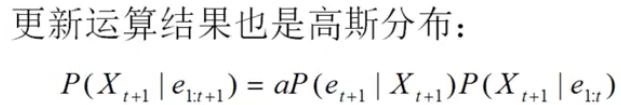
(拆分成t+1时刻的证据和1~t时刻的证据再利用一个贝叶斯公式)
更新运算结果就是 新来的一个t+1时刻的证据
来估计t+1时刻的状态
相当于对状态进行了更新
四、一维实例
1.
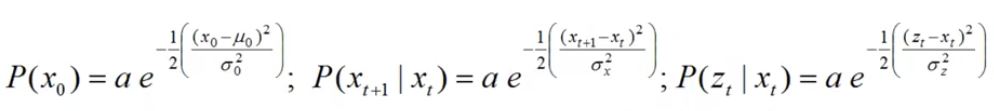
先验分布 一个一维高斯分布它的均值是μ0 方差是σ0平方
转移模型 一个线性高斯分布它的均值是Xt方差是σx平方
观察模型 一个高斯分布它的均值是Xt 方差是σz平方
2.
根据零时刻的状态分布以及转移模型,
可以对1时刻的状态分布进行预测:
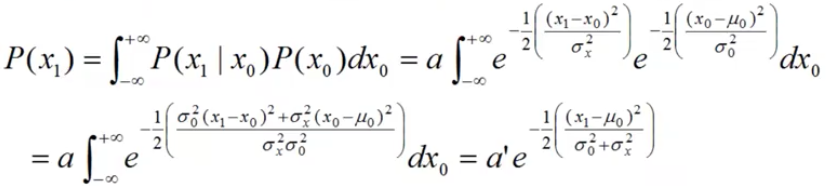
解释:
零时刻的状态分布乘以这个转移模型
再对零时刻的状态进行积分
再把两个分布代进来
3.滤波
得到1时刻的证据z1之后
对1时刻的状态分布进行更新(就是滤波)
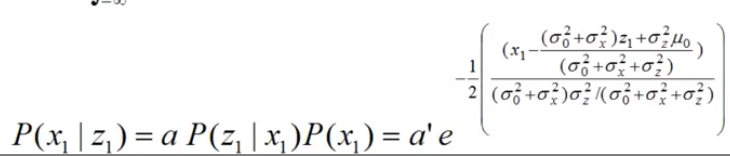
对1时刻状态的更新也是一个高斯分布
1时刻的均值μ1
1时刻的方差σ1
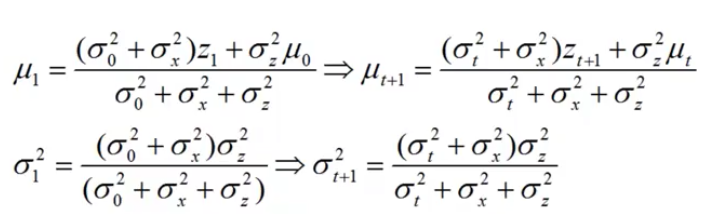
朝闻道


 浙公网安备 33010602011771号
浙公网安备 33010602011771号