隐马尔科夫模型

一、问题

状态随时间变化，需要跟踪、预测

二、基本思想

在每个时间点，根据新的证据变量来更新世界状态

三、时间上的概率推理

建立 转移模型、传感器模型、先验概率分别

1.转移模型

世界如何演变，在描述了给定过去的时间的世界状态下，当前时间世界的状态变量

2.传感器模型，观察模型

描述了给定当前世界状态条件下，每个感知的概率分布

3.先验概率分布

即 世界是如何开始的

四、马尔科夫模型

当前时刻的状态只依赖与前一时刻的状态

当前时刻感知到的证据变量的分布只依赖与当前时刻

五、

一阶马尔科夫模型的贝叶斯网络形式

 

随机变量有时间下标（动态贝叶斯网络）

 

状态变量：下雨、不下雨的 bool型变量（t:ture  f:false）

观察变量：带伞、不带伞的bool型变量

转移模型：上边的表格（前一时刻在不同的取值下，当前时刻的概率分布）

                  解读：前一时刻下雨，当前时刻下雨的概率为0.7，不下雨为0.3；

                            前一时刻不下雨，当前时刻下雨的概率为0.3，不下雨为0.7

传感器模型：下边的表格（当前状态在不同的取值情况下，证据变量的概率分布表）

                      解读：当前时刻下雨的情况下，带伞的概率为0.9，不带伞0.1

                                当前时刻不下雨，带伞的概率0.2，不带伞的概率0.8

推理

1-滤波推理

 

2-预测（预测未来）

3-平滑（理解过去）

 

滤波推理：根据到目前为止观察到的证据来估计当前状态

预测：根据到目前为止感知到的证据来预测未来

平滑：根据到目前为止收集到的证据去重新计算过去某一时刻的概率分布

 

滤波公式：

 

六、滤波示例

 

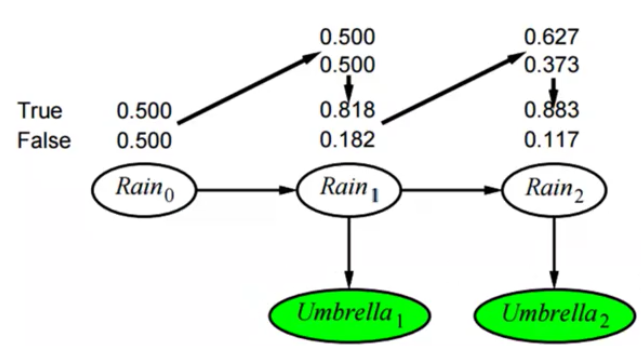
假设：一个人在房间里没有办法观察到外面的天气

只能根据进来的人有没有带伞来判断有没有下雨

状态变量：有没有下雨
证据变量：有没有带伞

初始这一天在没有任何证据情况下
我们设定：下雨的概率是0.5，不下雨的概率是0.5

 

第一天它观察到有人带伞了

问题：

第一天下雨的概率是多少？不下雨的概率是多少？

利用滤波公式

首先根据零时刻的状态估计乘以转移模型

得到这么一个分布（0.500 0.500）

然后再根据它观察到了带伞了
利用传感器模型乘以（0.500 0.500）分布
就得到了下雨的概率是0.818 不下雨的概率是0.182分布（0.818 0.182）

 

 

（0.818 0.182）：第一天的状态估计

 

第二天它又观察到带伞了
把第一天的状态估计（0.818 0.182）
乘以转移模型得到（0.627 0.373）状态估计

再根据第二天观察到带伞了
乘以观察模型就得到了下雨的概率是0.883 不下雨的概率是0.117分布（0.833 0.117）

 

七、总结

隐马尔可夫模型就是一种特定表达的马尔可夫模型

它的状态变量是一个 它的证据变量也只有一个

 

 

 

八、矩阵表达

 转移模型

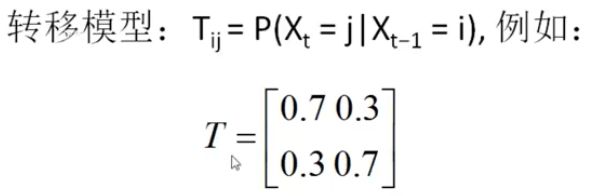
状态变量的值域是1~s   它有s个不同的取值

把这些s个不同的取值按顺序编好号

比如前面的例子
状态变量下不下雨的值域是true和false
假设第一种值表示true 第二种值表示false

转移模型就可以表达成一个s行s列的方阵

 用T来表示 那它的第i行第j列的值表达的就是

前一时刻取第i种值     这一时刻取第j种值的概率
比如说

这个方阵就是那个下不下雨的转移模型 

0.7表示的就是第一行第一列
第一行表示的是前一天它取第一种值也就是下雨,前一天下雨

那么第一列表示的就是

当天也取第一种值 就是下雨

那么这个0.7就表示前一天下雨当天也下雨的概率是0.7

 

 传感器模型

 

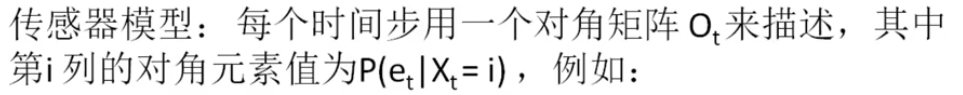
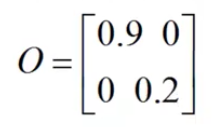
传感器模型也可以用一个矩阵来表示
这个矩阵是一个对角矩阵 我们用O来表示

 

对角矩阵的第i列的对角元素值表示的是

当前时刻取第i种状态情况下观察到当前证据的概率

比如

0.9表示的就是当前时刻取第一种值

当前时刻下雨 （观察到当前证据 我们的证据变量是带不带伞）

观察到带伞的概率是0.9

第二列就是 当前时刻等于第二种值
也就是当前时刻不下雨观察到带伞的概率是0.2

 

九、矩阵运算

转移模型和传感器模型都用矩阵表示出来
推理运算就全部可以变成矩阵运算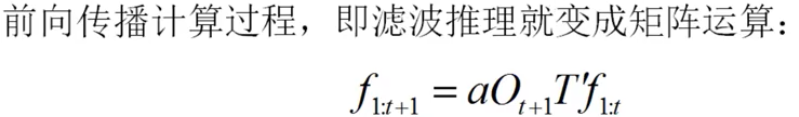

t+1时刻的滤波就等于

一个归一化因子乘以t+1时刻的传感矩阵再乘以转移矩阵的转置再乘以t时刻的状态估计