某零件上有一段曲线，为了在程序控制机床上加工这一零件

 

1．

 

 

x=20:5:65;

X=[ones(10,1) x'];

Y=[13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3]';

[b,bint,r,rint,stats]=regress(Y,X);

 

b =

 

    9.1212

    0.2230

 

bint =

 

    8.0211   10.2214

    0.1985    0.2476

 

stats =

 

0.9821  439.8311    0.0000    0.2333

c=x';

[p,S]=polyfit(c,Y,1);

[A,DELTA]=polyconf(p,42,S,0.05)

A =

 

   18.4885

DELTA =

 

1.1681

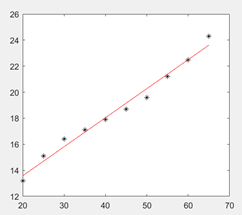
得Y关于X的线性回归方程:Y=9.1212+0.2230X

0.9821很接近1,所以回归效果显著.

A=18.4885

DELTA=1.1681

故当x=42C时它的产量估值为18.4885

预测区间(置信度95%) 为:[17.3204;19.6566]

绘图：

 

 

2.

某零件上有一段曲线，为了在程序控制机床上加工这一零件，需要求这段曲线的解析表达式，在曲线横坐标xi处测得纵坐标yi共11对数据如下：

 

 

求这段曲线的纵坐标y关于横坐标x的二次多项式回归方程.

代码：

x=0:2:20;

y=[0.6,2.0,4.4,7.5,11.8,17.1,23.3,31.2,39.6,49.7,61.7];

[p,S]=polyfit(x,y,2)

 

p =

 

0.1403    0.1971    1.0105

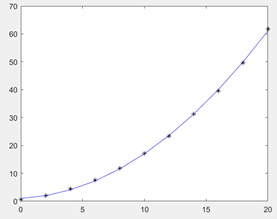
所以回归模型为：y=0.1403*x^2+0.1971*x+1.0105 

绘图：