水塔流量问题
一、问题重述
某居民区有一供居民用水的圆形水塔，一般可以通过测量其水位来估计水的流量。但面临的困难是，当水塔水位下降到设定的最低水位时，水泵自动启动向水塔供水，到设定的最高水位时停止供水，这段时间是无法测量水塔的水位和水泵的供水量。通常水泵每天供水一两次，每次约两小时。水塔是一个高12.2米、直径17.4米的正圆柱。按照设计，水塔水位降到约8.2米时，水泵自动启动，水位升到约10.8米时水泵停止工作。
某一天的水位测量记录如表1所示，试估计任何时刻（包括水泵正供水时）从水塔流出的水流量，及一天的总用水量。
二、问题分析
1）拟合水位与时间函数
对非供水时段进行多项式（3~6）拟合。
2）确定流量与时间函数
在水泵不工作时段，流量通过水位与时间的变化率求解；
在水泵工作时段，流量通过供水时段流量拟合得到。
3）估计一天总用水量
总水量等于供水时段和非供水时段流量对时间的函数积分之和。
三、模型求解
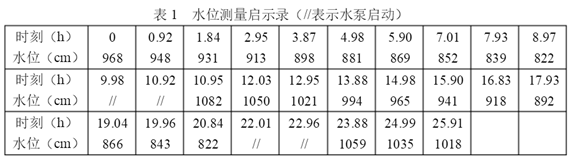
1、拟合非供水时段的水位，导出其流量
拟合第一段水位
>> t=[0 0.92 1.84 2.95 3.87 4.98 5.9 7.01 7.93 8.97 10.95 12.03 12.95 13.88 14.98 15.90 16.83 17.93 19.04 19.9 20.84 23.88 24.99 25.91];
h=[968 948 931 913 898 881 869 852 839 822 1082 1050 1021 994 965 941 918 892 866 843 822 1059 1035 1018];
>> c1=polyfit(t(1:10),h(1:10),3)
a1=polyder(c1)
c1 =
-0.0785 1.3586 -22.1079 967.7356
a1 =
-0.2356 2.7173 -22.1079
%其中a1系数为流量函数系数
>> tp1=0:0.1:9;
x1=-polyval(a1,tp1);
>> plot(tp1,x1,'c.')
>> axis([0 25 12 34])
xlabel('小时')
ylabel('厘米/小时')
>> hold on
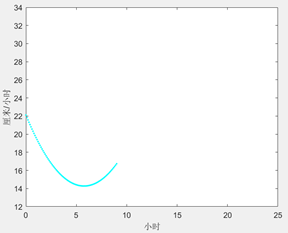
拟合第二段水位
>> t=[0 0.92 1.84 2.95 3.87 4.98 5.9 7.01 7.93 8.97 10.95 12.03 12.95 13.88 14.98 15.90 16.83 17.93 19.04 19.9 20.84 23.88 24.99 25.91];
h=[968 948 931 913 898 881 869 852 839 822 1082 1050 1021 994 965 941 918 892 866 843 822 1059 1035 1018];
>> c2=polyfit(t(10.9:21),h(10.9:21),4)
a2=polyder(c2)
c2 =
1.0e+03 *
-0.0000 0.0003 -0.0044 -0.0018 1.3644
a2 =
-0.0186 0.7529 -8.7512 -1.8313
%其中a2系数为流量函数系数
>> tp2=10.9:0.1:21;
x2=-polyval(a2,tp2);
plot(tp2,x2,'c.')
>> hold on
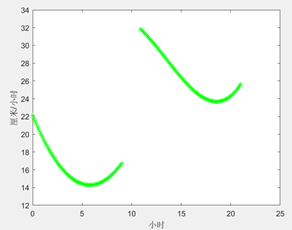
2、拟合供水时段的流量
1）拟合第一供水时段
>> xx1=-polyval(a1,[8 9]);
xx2=-polyval(a2,[11 12]);
xx12=[xx1 xx2];
a12=polyfit([8 9 11 12],xx12,3)
a12 =
1.0e+03 *
-0.0012 0.0368 -0.3551 1.1363
%其中a12系数为流量函数系数
>> tp12=9:0.05:11;
x12=polyval(a12,tp12);
plot(tp12,x12,'R.')
>> hold on
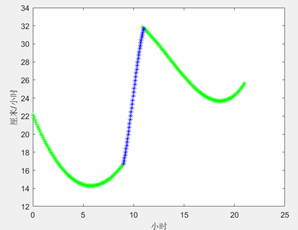
2）拟合第二供水时段
>> dt3=diff(t(22:24));
dh3=diff(h(22:24));
dht3=-dh3./dt3;
t3=[20 20.8 t(22) t(23)];
xx3=[-polyval(a2,t3(1:2)),dht3];
a3=polyfit(t3,xx3,3)
a3 =
0.0468 -3.6538 91.8283 -725.3839
%其中a3系数为流量函数系数
>> tp3=20.8:0.05:24;
x3=polyval(a3,tp3);
plot(tp3,x3,'R.');
hold on
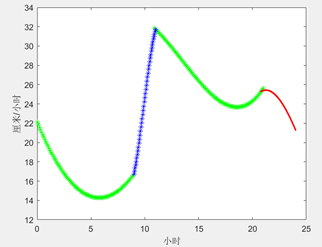
3、估计一天总用水量
>> y1=0.1*trapz(x1)
y2=0.1*trapz(x2)
y12=0.1*trapz(x12)
y3=0.1*trapz(x3)
y=(y1+y2+y12+y3)*237.8*0.01
y1 =
146.5150 %第一非供水时段用水量
y2 =
265.0009 %第二非供水时段用水量
y12 =
47.4086 %第一供水时段用水量
y3 =
68.2422 %第二供水时段用水量
y =
1.2536e+03 %总用水量检验模型可信度
1）根据非供水时段水位差与所得相等进行估计。
#第一非供水时段：
968-822=146 ~ 146.5150
#第二非供水时段：
1082-822=260 ~265.0009
2）根据供水时段泵水功率相等进行估计。
#第一供水时段：
功率为：（47.406+260）/1.98=155.28
#第二供水时段：
功率为：（68.2422+237）/1.87=163.23
四、结果分析
本题根据已给数据通过曲线拟合的方式绘制了居民用水曲线，通过观察图像，可看出用水在中午及晚上出现两个高峰，与生活实际相符。
