激活函数
1. 激活函数概念
所谓激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。引入激活函数是为了增加神经网络模型的非线性，使得神经网络可以任意逼近任何非线性函数。
2. 常用激活函数
阶跃函数
最简单的激活函数，图像如下。在单层感知机中，常用该激活函数处理线性可分问题（如逻辑与，非，或门等问题），对于非线性问题，需要采用其他非线性激活函数，此时就是神经网络了。
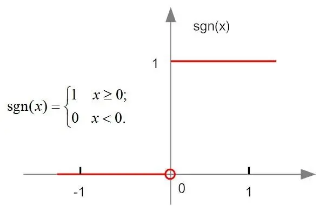
优点：可以使用它处理线性问题。
缺点：函数不光滑，不连续，不是处处可导。
Sigmoid函数
Sigmoid函数曾经最早用于神经网络中，也叫Logistic 激活函数，现阶段神经网络更多地使用ReLu激活函数。Sigmoid函数公式如下：
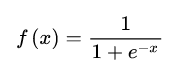
对应的函数图如下：
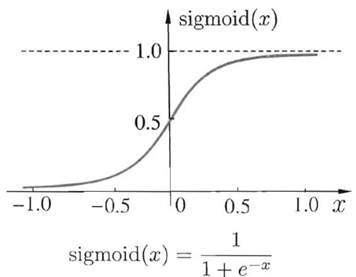
其导数图像如下图：
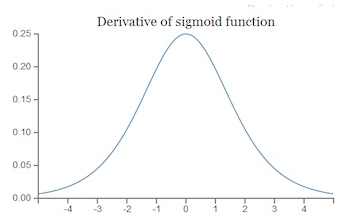
通过导数图可以发现，sigmoid最大的导数值为0.25，随着神经网络层次加深，反向传播链式求导累乘得到的导数逐渐变小，从而导致梯度几乎消失，造成靠近输入端的参数几乎得不到更新。
缺点：
- 会有梯度弥散（当X值比较大时，梯度逐渐趋近于0），导致梯度几乎消失。
- 不是关于原点对称，
- 由于有指数e，计算耗时。
优点：
1.连续平滑单调容易求导
2.输出值在0到1之间，方便观察输出是否符合预期，适合作为概率模型的输出。
Tanh函数
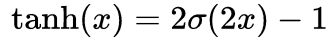
带入sigmoid可以得到具体函数形式如下：
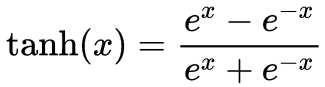
其函数图像如下图所示：
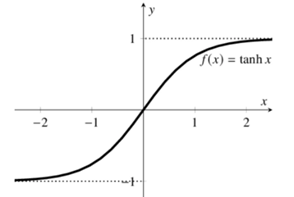
可以看到tanh取值范围在[-1,1]之间。
优点：Tanh解决了Sigmoid的输出是不是零中心的问题，但仍然存在饱和问题。
缺点：tanh并没有解决sigmoid梯度消失的问题。
为了防止饱和，现在主流的做法会在激活函数前多做一步batch normalization，尽可能保证每一层网络的输入具有均值较小的、零中心的分布。
ReLu函数
噪声线性整流（Noisy ReLU）是修正线性单元在考虑高斯噪声的基础上进行改进的变种激活函数，也是现在用的最多的一种激活函数。
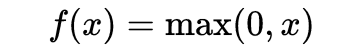
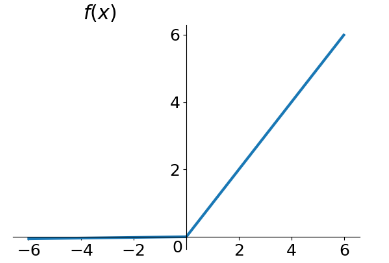
导数入下图：
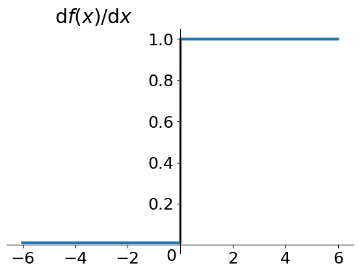
ReLu的优点：
1．在X>0时，由于导数为1，链式法则连乘也不会导致梯度消失，解决了梯度消失的问题。
2. 计算方便，不存在指数计算，计算速度快 ，加速了网络的训练。
3. 在SGD中收敛速度要比Sigmoid和tanh快很多。
ReLu缺点：
1. 由于负数部分恒为0，大的学习率会导致一些神经元永久性死亡，无法激活（可通过设置小学习率部分解决）。
2. 输出不是以0为中心的。
注意：关于大的学习率导致“神经元永久性死亡”如何理解呢？
首先我们知道参数更新是通过W=W-α*(W导数)，若学习率α太大，会导致W更新后为负数，当输入某个正值时，会导致其与W相乘后仍然为负值，此时激活函数输出为0，而此时的导数也为0，下次反向传播链式法则更新参数时，由于梯度为0，W将永远得不到更新。
LeakReLU激活函数
为了弥补当学习率过大时会出现某些神经元永久死亡，导致网络后期参数无法正常更新的现象。改进了ReLu，公式与图对应如下。α一般为0.01到0.2取值，为负轴的正斜率。即使出现负值输入，也能反向传播。公式与图入下：
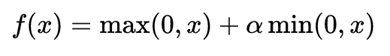
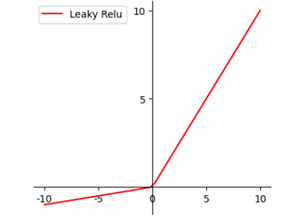
优点：
1.具有ReLu激活函数的优点。
2.解决了Relu会杀死一部分神经元的情况。
缺点：
1.结果不一致，无法为正负输入提供一致的关系预测。
小结：通过使用ReLU函数作为激活函数可以避免梯度消失的问题。另外梯度剪切、Batch Normalization(批量归一化)也可以有效避免梯度爆炸问题，BN也能有效避免一定程度sigmoid中梯度消失问题，sigmoid因为容易存在梯度弥散与爆炸问题，往往也作为分类任务输出层的激活函数，将值映射到0~1概率区间。ReLu仍然是目前使用最多的激活函数。在NLP中，主要使用Tanh函数。除了上面的激活函数外，还有ELU、SELU、swish激活函数。
若存在不足或错误之处，欢迎指正与评论！
参考资料：
https://zhuanlan.zhihu.com/p/32610035
https://baike.baidu.com/item/%E6%BF%80%E6%B4%BB%E5%87%BD%E6%95%B0/2520792?fr=aladdin
https://blog.csdn.net/weixin_39612726/article/details/111391713
