K近邻算法(KNN)

1. k近邻算法(K-Nearest Neighbor，KNN)

　　K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：在特征空间中，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别。如下图所示：

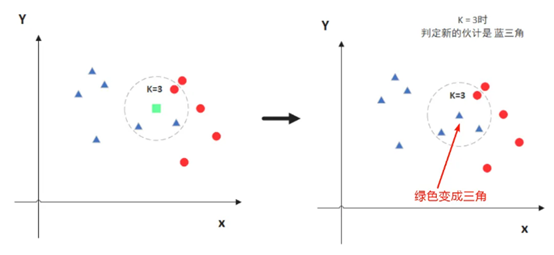
2. 距离函数的定义

　　在多维空间中，KNN使用的是欧氏距离度量周围样本距离预测样本的距离。公式如下：

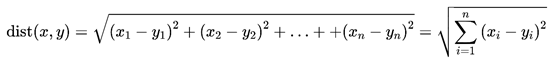
3. KNN实现鸢尾花(Iris)分类

　　先看一下，鸢尾花长这样子。

　　鸢尾花数据集记录了三类花以及它们的四种属性。（四种属性：花萼长度，花萼宽度，花瓣长度，花瓣宽度；3种标签：Setosa，versicolor，virginica）

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

iris_dataset = load_iris()  # 载入数据集
feature = iris_dataset['data']
target = iris_dataset['target']
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=0)
print(x_train)
print(y_train)#标签0,1,2表示三种不同的花卉(山鸢尾、变色鸢尾、维吉尼亚鸢尾)
knn = KNeighborsClassifier(n_neighbors=3)
knn = knn.fit(x_train, y_train)
y_pred = knn.predict(x_test)
print('模型的分类结果:', y_pred)
print('真实的分类结果:', y_test)
predict_result=knn.predict([[6.1, 3.1, 4.7, 2.1]])
print(predict_result)#结果是2，维吉尼亚鸢尾

4. KNN实现手写数字识别分类

　　手写数字中用到的数据集为minist手写数字数据集，每张图片大小为28*28灰度图片。训练集为6万张，测试集为1万张，类别为0~9。

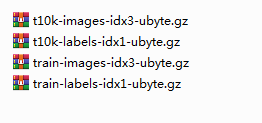
　　一共包含四个文件：

　　train-images-idx3-ubyte.gz：训练集图像（9912422 字节）55000张训练集 + 5000张验证集；

　　train-labels-idx1-ubyte.gz：训练集标签（28881 字节）训练集对应的标签；

　　t10k-images-idx3-ubyte.gz：测试集图像（1648877 字节）10000张测试集；

　　t10k-labels-idx1-ubyte.gz：测试集标签（4542 字节）测试集对应的标签；

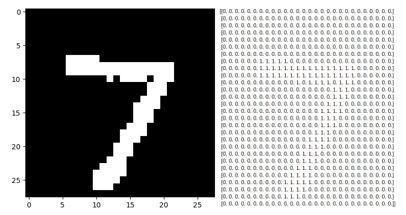
　　比如读取其中一个数据，转换为向量形式，这里我把向量放在了txt中，如图所示，很显然代表数字0.

　　由于是灰度图（一个通道），数字范围为0~255，进一步，可以将向量表示的图像进行阈值二值化，变为0与1，如下图：

　　代码实现：

import gzip
import numpy as np
import matplotlib.pyplot as plt
import cv2

def readImage(path,num_images=1):
    f=gzip.open(path,'r')
    image_size = 28
    f.read(16)#前16个字节存储的是magic number，number of images，number of rows ，number of columns
    buf=f.read(image_size * image_size * num_images)
    data=np.frombuffer(buf,dtype=np.uint8).astype(np.float32)#ndarray类型
    print("data",type(data))
    data=data.reshape(num_images,image_size,image_size,1)
    image = np.asarray(data).squeeze()
    return image


def readLabel(path,num_images=1):
    f = gzip.open(path,'r')
    f.read(8)
    labels=[]
    for i in range(0,num_images):
        buf = f.read(1)
        label = np.frombuffer(buf, dtype=np.uint8).astype(np.int64)
        labels.append(label)
    return  labels

def calEuclidean(x, y): #计算两向量的欧氏距离
    dist = np.sqrt(np.sum(np.square(x-y)))   # 注意：np.array 类型的数据可以直接进行向量、矩阵加减运算。np.square 是对每个元素求平均
    return dist

def knn(test,train,trainLabel,k):   #给定任意一个图片的向量采用k近邻求得所属类别,k表示距离最近的K的元素
    distAll=[]
    for i in range(0,len(train)):
        dist=calEuclidean(test,train[i])
        distAll.append(dist)
    #对距离排序
    # print(distAll)
    distAllTuple = sorted(zip(distAll, range(len(distAll))))
    distAllTuple.sort(key=lambda t: t[0])  #
    sort_distAll_position = [x[1] for x in distAllTuple]  # 得到排序后原来的下标，方便后面找label
    # print(sort_distAll_position)
    #计算前k个哪个类别出现的最多
    labelNum={}
    for i in range(0,k):
        if str(trainLabel[sort_distAll_position[i]][0]) not in labelNum:
            labelNum[str(trainLabel[sort_distAll_position[i]][0])]=1
        else:
            labelNum[str(trainLabel[sort_distAll_position[i]][0])]+=1
    print("在最近的k个元素中，每个类别出现的频率为",labelNum)
    return max(labelNum,key=labelNum.get)#返回数字最大所对应的类别

def accuracy(predictResult,testlabels):
    all = len(predictResult)
    TP = 0
    for i in range(0,len(predictResult)):
        if str(testlabels[i][0])== predictResult[i]:
            TP+=1
    return TP/all


if __name__=="__main__":
    path1='MNIST_data/train-images-idx3-ubyte.gz'
    # num_images=60000
    num_images = 1000
    imageArray=readImage(path1,num_images)#得到的是num个图像的向量
    # retval, dst = cv2.threshold(imageArray[1], 50, 1, cv2.THRESH_BINARY)#可以对图像阈值处理，处理第2个图片为二值图像
    retval, dst = cv2.threshold(imageArray, 50, 1, cv2.THRESH_BINARY)  # 可以对所有图像阈值处理，处理为二值图像
    # plt.imshow(imageArray,cmap='Greys_r')
    # plt.imshow(dst, cmap='Greys_r')
    # print(dst)
    # plt.show()
    labels=readLabel('MNIST_data/train-labels-idx1-ubyte.gz',1000)
    # print(labels[1])#类别为0
    imageArraytest = readImage('MNIST_data/t10k-images-idx3-ubyte.gz', num_images=100)#读取100个测试图片
    testlabels=readLabel('MNIST_data/t10k-labels-idx1-ubyte.gz',100)#读取100个测试图片的标签
    retval, dsttest = cv2.threshold(imageArraytest, 50, 1, cv2.THRESH_BINARY)  # 可以对图像阈值处理，处理为二值图像
    # plt.imshow(imageArray,cmap='Greys_r')
    plt.imshow(dsttest[0], cmap='Greys_r')#显示7的图像
    print(dsttest[0])
    plt.show()
    #随便拿第一张图片测试
    labelResult=knn(dsttest[0], dst, labels, 100)
    print("预测的结果为",labelResult)#输出为7
    print("实际结果为",testlabels[0])
    #以下测试100个图片，并计算准确率
    predictResult=[]
    for i in range(0,100):
        labelResult = knn(dsttest[i], dst, labels, 100)
        predictResult.append(labelResult)
    print(predictResult)
    Pre_accuracy=accuracy(predictResult, testlabels)
    print("准确率",Pre_accuracy)