k-means聚类

1. k-means聚类

　　聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程，聚类就是一种发现这种内在结构的技术，聚类是建立在无类标记的数据上，是一种非监督的学习算法

　　k均值聚类算法（k-means clustering algorithm）是最著名的划分聚类算法，是一种迭代求解的聚类分析算法。由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

2. k-means算法步骤

　　(1) 从数据中随机选择K个对象分别作为K个类的聚类中心点。

　　(2) 将其他数据划归为距离自己最近的类中，得到K个聚类分组。

　　(3) 重新计算每个聚类的中心点

　　(4) 再根据新的中心点继续划分归类，重复迭代(重复2与3)，直至中心点不再改变或改变很小。

　　经过上述4个步骤后，得到的为在给定初始随机值K个对象条件下的聚类，此时误差平方和局部最小（K-means算法的K人为选取，直接决定了聚类的误差平方和损失）。上述四个步骤中（2）中的距离用欧式距离来度量。假设样本数据集中有n个对象，X={X1,X2,…Xn},每个对象具有m个维度的属性，某个对象到某个聚类中心的欧式距离计算如下：

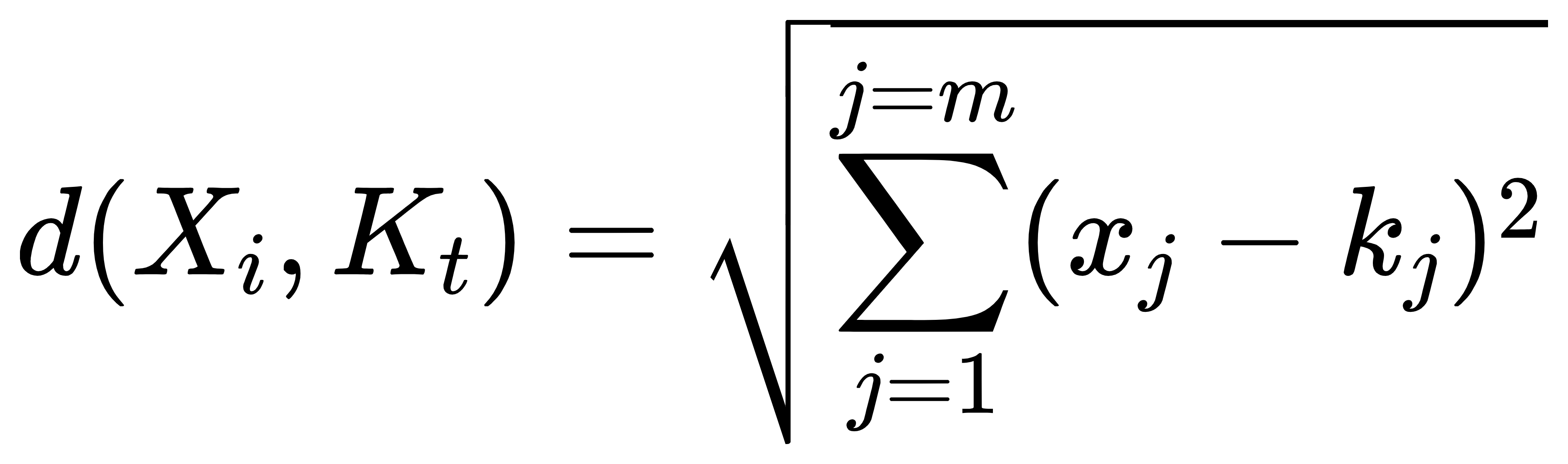
3.误差损失函数

　　记K个簇中心分别为K1,K2…Kc，每个簇的样本数量为N1,N2…Nc；则平方误差损失函数为：

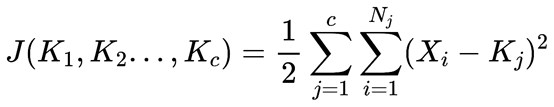
　　要获得最优解，就是目标损失函数函数尽可能小，现在对其中任意一个Kj求偏导，可以得到：

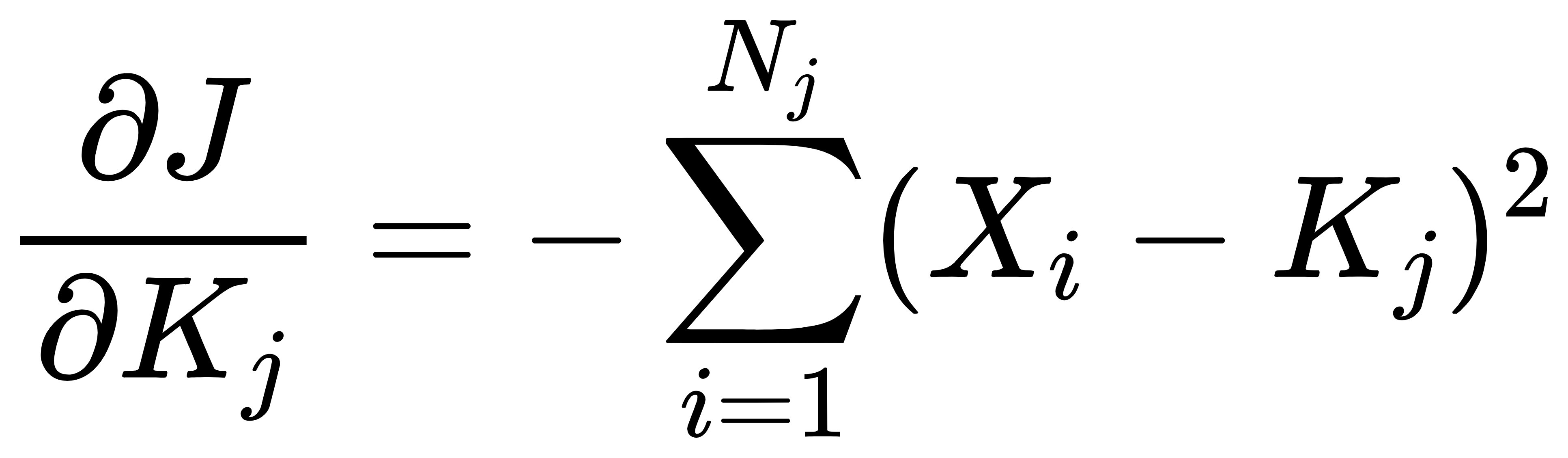
　　令偏导数等于0，得到：

　　可以看出，其是每个簇的中心（取该簇的每个属性的均值）。

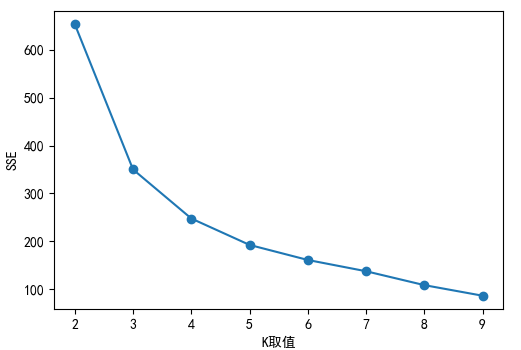
4. 手肘法

　　当选取的分类类别K值增加时，误差平方和SSE会出现骤减，随着K值继续增大，SSE趋于平缓。为了避免过拟合，手肘法即通过观察曲线(也可以计算多个拐点点斜率变化与各线段斜率大小)，选取拐点所对应的K值。

5.轮廓系数(Silhouette Coefficient)

　　在使用k-means聚类时，一般没有数据标签，完全依赖于评价簇内的稠密程度与簇间的离散程度来评估聚类效果的。常用轮廓系数来评估聚类算法模型的效果。数值越大。表明模型效果越好，为负值表明模型效果很差。轮廓系数计算公式如下：

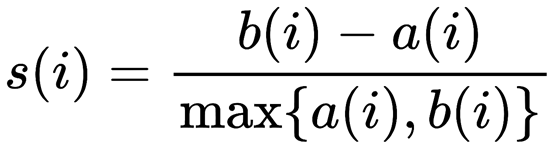
　　具体有如下：

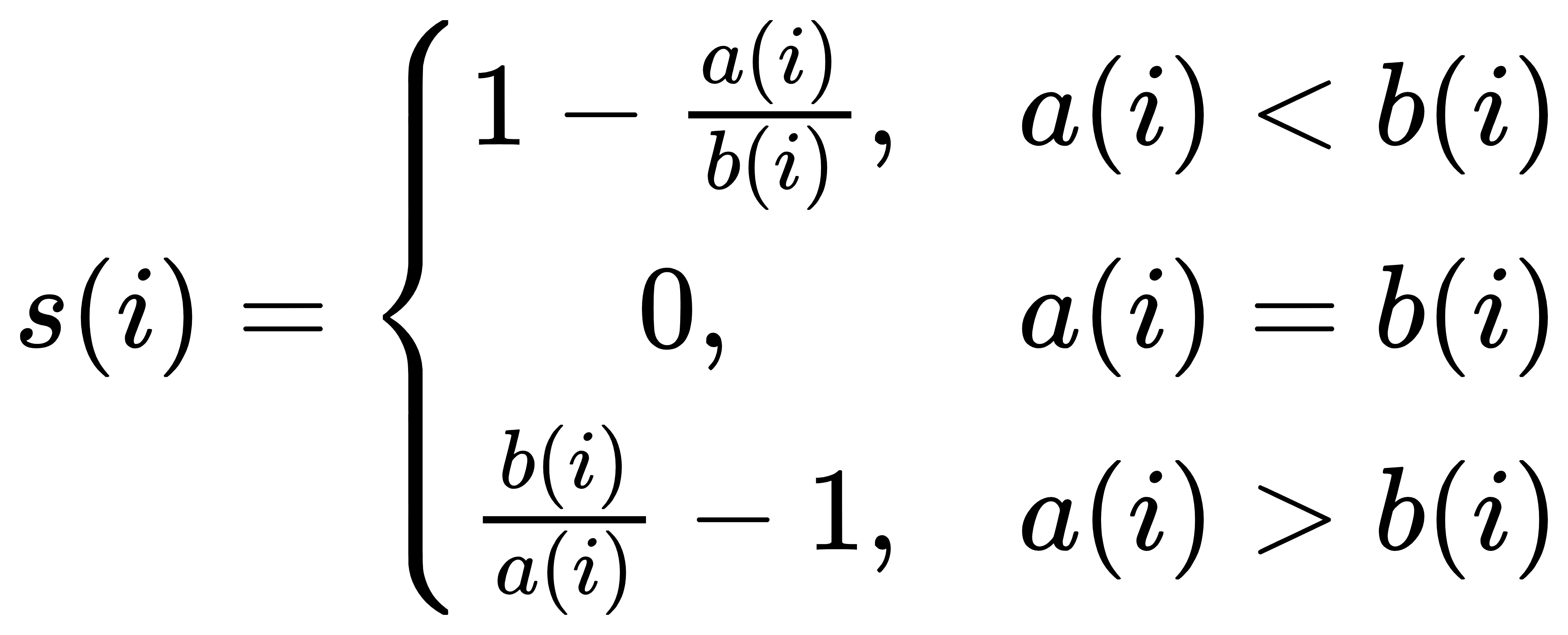
　　参数说明：

　　a(i)为第i个样本到同簇其他样本的平均距离，a(i)越小，说明i样本越应该被聚类到该簇，将a(i)称为样本的簇内不相似度。

　　b(i)为第i个样本到其他某簇Cj的所有样本的平均距离，记为bij，称为样本i与簇Cj的不相似度。定义第i个样本的簇间不相似度为

b(i)=min(bi1,bi2,…,bik}

　　S(i)越接近1，说明样本i聚类合理。

　　S(i)接近-1，则说明样本i更应该分类到另外的簇。

　　S(i)接近0，则说明样本i在两个簇的边界上。在实际计算中，将整个样本空间中所有样本的轮廓系数取算数平均值，作为聚类划分的性能指标S。

6.Kmeans算法优缺点

　　优点：原理简单，容易理解，聚类效果不错，收敛速度快；

　　　　　　当簇服从高斯分布时，效果很好。

　　缺点： K值由用户指定，不同的K值会得到不同的结果，不好把握；

对初始聚类中心敏感，不同的初始聚类中心有时候可能结果不同。

不适合发现非凸形状的簇或者大小差别较大的簇；

噪音数据、离群值对模型的影响较大；

复杂度与样本呈线性关系;

采用迭代的方法，只能找到局部最优解。

7.k-means图像演示

　　这里提供一个网站可以演示k-means。https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

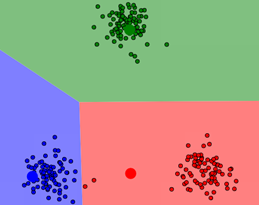
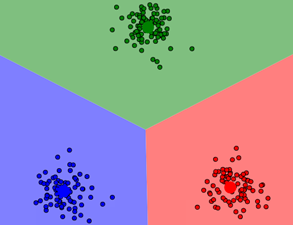
　　至此，聚类中心不再改变，k-means聚类结束。

8.k-means实现

from sklearn.cluster import KMeans
from sklearn import metrics
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

def readFile(path):
    df=pd.read_csv(path)
    return df

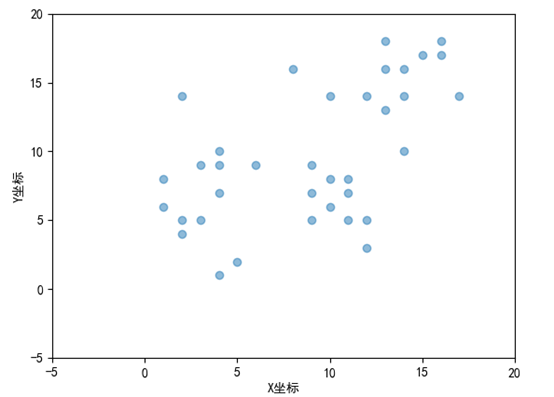
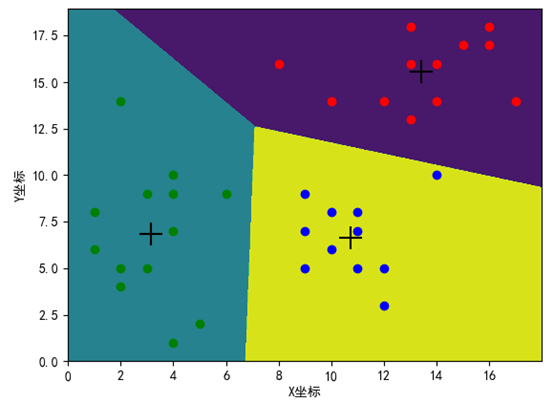
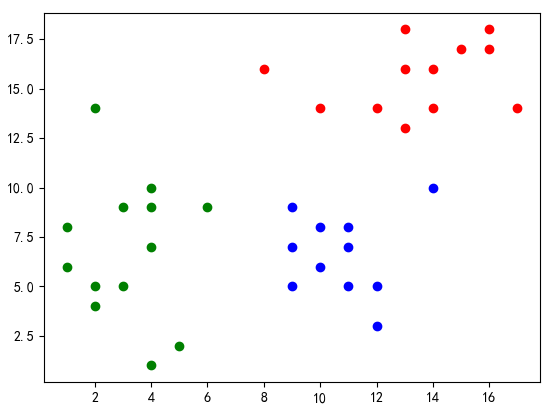
if __name__=='__main__':
    #读取数据
    df=readFile('data.csv')
    #绘制图形
    fig = plt.figure(1)
    colors = ['r', 'g', 'y', 'b', 'r', 'c', 'g', 'b', 'k', 'm']
    x=df.iloc[0:,0].to_list()
    print(x)
    print(type(x))
    y=df.iloc[0:,1].to_list()
    area = 20 * np.arange(1, 10)#设置点的面积大小 area 值
    widths = np.arange(10)  # 设置点的边界线宽度 0-9的数字
    plt.scatter(x, y,  alpha=0.5, marker='o')
    plt.xlabel('X坐标')
    # # 设置Y轴标签
    plt.ylabel('Y坐标')
    # 8. 设置图标题：title
    # plt.title('test绘图函数')
    # 9. 设置轴的上下限显示值：xlim、ylim
    # 设置横轴的上下限值
    plt.xlim(-5, 20)
    # 设置纵轴的上下限值
    plt.ylim(-5, 20)
    # plt.savefig('test_xx.png', dpi=200, bbox_inches='tight', transparent=False)
    plt.show()
    #调用kmeans聚类算法
    kms=KMeans(n_clusters=3)
    Xtrain=df.values   #转换为ndarray类型的[[ 2  5] [ 1  6] [ 5  2]....]数据
    print(type(Xtrain))
    kms.fit(Xtrain)
    Xtest=np.array([[3,5],[14,16],[8,4]])
    print("簇心={}".format(kms.cluster_centers_))  # 打印簇心
    print("预测结果：{}".format(kms.predict(Xtest)))  # 预测样本
    print("轮廓系数={}".format(metrics.silhouette_score(Xtrain, kms.labels_, metric='euclidean')))
    #绘制聚类后的图形
    # 获取标签
    label_kms = kms.labels_
    print(label_kms)
    x0,y0 = np.array(x)[label_kms == 0],np.array(y)[label_kms == 0]
    x1,y1 = np.array(x)[label_kms == 1],np.array(y)[label_kms == 1]
    x2,y2 = np.array(x)[label_kms == 2],np.array(y)[label_kms == 2]
    centers = kms.cluster_centers_  #聚类中心
    # 绘制聚类结果
    plt.scatter(x0, y0, c='red', marker='o', label='label0')
    plt.scatter(x1, y1, c='green', marker='o', label='label1')
    plt.scatter(x2,y2,  c='blue', marker='o', label='label2')
    plt.scatter(centers[:, 0], centers[:, 1], marker='+', c='black', alpha=1, s=300)
    plt.xlabel('X坐标')
    # # 设置Y轴标签
    plt.ylabel('Y坐标')
    plt.show()
    print(metrics.silhouette_score(Xtrain, kms.labels_, metric='euclidean'))
    #手肘法
    sse=[]
    silhouette=[]
    for k in range(2,10):
        kms = KMeans(n_clusters=k)
        kms.fit(Xtrain)
        sse.append(kms.inertia_)
        silhouette.append(metrics.silhouette_score(Xtrain, kms.labels_, metric='euclidean'))
        print(metrics.silhouette_score(Xtrain, kms.labels_, metric='euclidean'))
        print(type(metrics.silhouette_score(Xtrain, kms.labels_, metric='euclidean')))
    plt.plot(range(2, 10), sse, marker='o')
    plt.xlabel('K取值')
    # # 设置Y轴标签
    plt.ylabel('SSE')
    plt.show()
    print(silhouette)#不同K值下的轮廓系数[0.523, 0.523, 0.514, 0.445, 0.446, 0.443, 0.375, 0.392]
    # 绘制簇的作用域
    # 获取数据值所在的范围
    x_min, x_max = np.array(x).min() - 1, np.array(x).max() + 1
    y_min, y_max = np.array(y).min() - 1, np.array(y).max() + 1
    # 生成网格矩阵
    kms = KMeans(n_clusters=3)
    kms.fit(Xtrain)
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
    z = kms.predict(np.c_[xx.ravel(), yy.ravel()])
    z = z.reshape(xx.shape)
    cs = plt.contourf(xx, yy, z)
    x0, y0 = np.array(x)[label_kms == 0], np.array(y)[label_kms == 0]
    x1, y1 = np.array(x)[label_kms == 1], np.array(y)[label_kms == 1]
    x2, y2 = np.array(x)[label_kms == 2], np.array(y)[label_kms == 2]
    centers = kms.cluster_centers_  # 聚类中心
    # 绘制聚类结果
    plt.scatter(x0, y0, c='red', marker='o', label='label0')
    plt.scatter(x1, y1, c='green', marker='o', label='label1')
    plt.scatter(x2, y2, c='blue', marker='o', label='label2')
    plt.scatter(centers[:, 0], centers[:, 1], marker='+', c='black', alpha=1, s=300)
    plt.xlabel('X坐标')
    # # 设置Y轴标签
    plt.ylabel('Y坐标')
    plt.show()

9.k-means图像压缩

　　先对图像的每个像素运行K-Means算法，然后将每个像素映射为最近的质心。

from skimage import io
from sklearn import cluster
from sklearn.cluster import KMeans
import numpy as np
import cv2
import matplotlib.pyplot as plt
# image = io.imread("Lenna.jpg")
"""
cv2.IMREAD_COLOR：加载彩色图片，这个是默认参数，可以直接写1。
cv2.IMREAD_GRAYSCALE：以灰度模式加载图片，可以直接写0。
cv2.IMREAD_UNCHANGED：包括alpha(包括透明度通道)，可以直接写-1
"""
img=cv2.imread('lenna.jpg',1)
print(img.shape)
data=img.reshape((-1,3)) #这里-1就是由图片某个通道的像素决定，相当于长*宽像素，每一列代表一个通道像素
dataFloat32=np.float32(data)

print(cv2.TERM_CRITERIA_EPS)
print(cv2.TERM_CRITERIA_MAX_ITER)
#定义终止条件(type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
#随机选定初始中心
flags = cv2.KMEANS_RANDOM_CENTERS

"""
函数原型：

retval, bestLabels, centers = kmeans(data, K, bestLabels, criteria, attempts, flags, centers=None)

函数参数：

data:  需要分类数据，最好是np.float32的数据，每个特征放一列。

K:  聚类个数 

bestLabels：预设的分类标签或者None

criteria：迭代停止的模式选择，这是一个含有三个元素的元组型数。格式为（type, max_iter, epsilon） 其中，type有如下模式：
cv2.TERM_CRITERIA_EPS ：精确度（误差）满足epsilon，则停止。
cv2.TERM_CRITERIA_MAX_ITER：迭代次数超过max_iter，则停止。
cv2.TERM_CRITERIA_EPS+cv2.TERM_CRITERIA_MAX_ITER：两者结合，满足任意一个结束。
attempts：重复试验kmeans算法次数，将会返回最好的一次结果
flags：初始中心选择，可选以下两种：
cv2.KMEANS_PP_CENTERS：使用kmeans++算法的中心初始化算法，即初始中心的选择使眼色相差最大.详细可查阅kmeans++算法。(Use kmeans++ center initialization by Arthur and Vassilvitskii)
cv2.KMEANS_RANDOM_CENTERS：每次随机选择初始中心（Select random initial centers in each attempt.）

返回值
retval：距离值（也称密度值或紧密度），返回 每个点到相应中心点距离的平方和(是一个数)。
bestLabels：各个数据点的最终分类标签（索引）。
centers：每个分类的中心点数据。

"""

#K-Means聚类 聚集成2类
compactness, labels4, centers4 = cv2.kmeans(dataFloat32, 4, None, criteria, 10, flags)
print(labels4)

centers4 = np.uint8(centers4)
print(centers4)
res = centers4[labels4.flatten()]
dst4 = res.reshape((img.shape))

#图像转换为RGB显示
"""
OpenCV 使用 BGR 格式，matplotlib/PyQt 使用 RGB 格式。使用 matplotlib/PyQt 显示 openCV 图像，要将 BGR 格式转换为 RGB 格式
plt.imshow() 可以直接显示 OpenCV 灰度图像，不需要格式转换，但需要使用 cmap=‘gray’ 进行参数设置。
"""
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
dst4 = cv2.cvtColor(dst4, cv2.COLOR_BGR2RGB)
plt.subplot(1,2,1)
plt.imshow(img)
plt.xticks([]), plt.yticks([])

plt.subplot(1,2,2)
plt.imshow(dst4)
plt.xticks([]), plt.yticks([])
plt.show()

10.k-means++

　　K-Means++与K-means在选取初始聚类中心时做法不同，K-means是随机的，由于KMeans 算法对初值敏感，对于不同的初始值，可能会导致不同的聚类结果。若初始化是个随机过程，有可能每个簇中心都在同一个簇中，这种情况 KMeans 聚类算法很大程度上都不会收敛到全局最小。K-Means++算法在聚类中心的初始化过程中的基本原则是使得初始的聚类中心之间的相互距离尽可能远，具体做法是随机初始化第一个聚类中心，每次增加的聚类中心离所有聚类中心尽可能远。算法具体做法如下：

从数据即X中随机（均匀分布）选取一个样本点作为第一个初始聚类中心 C1。
计算每个样本与当前已有聚类中心之间的最短距离D(X)；再计算每个样本点被选为下个聚类中心的概率P(X) ，最后选择最大概率值所对应的样本点作为下一个簇中心。

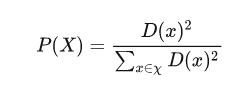
　　重复上步骤，直到选择 K个聚类中心。

小结：对于kemans，类别个数相同时，不同的初始中心值有时也可能得到不同的聚类结果。选定初始中心值后，经过有限次迭代，是一定可以收敛的（因为目标误差函数是凸函数）。由于不同初始值中心点，可能会造成不同的结果，所以得到的结果可能是局部最优。

参考资料：

https://blog.csdn.net/q923714892/article/details/117357187

https://blog.51cto.com/u_14926062/5323784

https://blog.csdn.net/youcans/article/details/121169102

https://zhuanlan.zhihu.com/p/342052190

附上代码与数据：链接：https://pan.baidu.com/s/16Td4f2223J5DIGktBLOaqg 提取码：p0kz

　　不足之处，恳请指正，有帮助请帮点赞!

posted @ 2022-11-19 13:00 wancy 阅读(1649) 评论(0) 编辑收藏举报

刷新页面返回顶部

wancy

k-means聚类

公告