动态规划

1.动态规划概念与基本思想

　　动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

2.动态规划基本要素

　　最优子结构：如果一个问题满足最优性原理通常称此问题具有最优子结构性质。也就是问题的最优解包含其子问题的最优解。

　　重叠子问题：递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算。这种性质称为子问题的重叠性质。动态规划算法避开了递归时，重复的计算相同子问题的过程，对每个子问题只解一次，而后将其保存在一个表格中，当再次需要的时候，只是简单的用常数时间查看一下结果。采用动态规划只需要多项式的时间，获得较高的解题效率。

　　备忘录方法：为避免相同的子问题的重复求解，采用备忘录方法为没格子问题建立一个记录项。动态规划采用自底向上的方式求解问题。求解每一级子问题的最优值填入备忘录。

3.多段图的最短路径问题

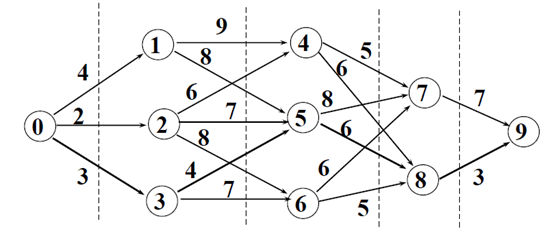
　　多段图的最短路径问题是求从源点到终点的最小代价路径。(关于多段图问题是满足最优性原理的。)

　　下面使用动态规划分析：　

　　对多段图的边(u, v)，用C_uv表示边上的权值，将从源点s到终点t的最短路径记为d(s, t)，则从源点0到终点9的最短路径d(0, 9)由下式确定：

　　d(0, 9)=min{c01+d(1, 9), c02+d(2, 9), c03+d(3,9)}

　　d(0, 9)依赖于d(1,9)、d(2,9)、d(3,9) 而

　　d(1, 9)=min{c14+d(4, 9), c15+d(5, 9)}

　　d(2, 9)=min{c24+d(4, 9), c25+d(5, 9), c26+d(6, 9)}

　　d(3, 9)=min{c35+d(5, 9), c36+d(6, 9)}

　　这一阶段的决策又依赖于d(4, 9)、d(5, 9)和d(6, 9)

　　的计算结果：

　　d(4, 9)=min{c47+d(7, 9), c48+d(8, 9)}

　　d(5, 9)=min{c57+d(7, 9), c58+d(8, 9)}

　　d(6, 9)=min{c67+d(7, 9), c68+d(8, 9)}

　　这一阶段的决策依赖于d(7, 9)和d(8, 9)的计算，而d(7, 9)和d(8,9)可以直接获得（括号中给出了决策产生的状态转移）：

　　d(7, 9)=c79＝7(7→9)

　　d(8, 9)=c89＝3(8→9)

　　再向前推导，有：

　　d(6, 9)=min{c67+d(7, 9), c68+d(8, 9)}=min{6+7, 5+3}=8(6→8)

　　d(5, 9)=min{c57+d(7, 9), c58+d(8, 9)}=min{8+7, 6+3}=9(5→8)

　　d(4, 9)=min{c47+d(7, 9), c48+d(8, 9)}=min{5+7, 6+3}=9(4→8)

　　d(3, 9)=min{c35+d(5, 9), c36+d(6, 9)}=min{4+9, 7+8}=13(3→5)

　　d(2, 9)=min{c24+d(4, 9), c25+d(5, 9), c26+d(6, 9)}=min{6+9,7+9, 8+8}=15(2→4)

　　d(1, 9)=min{c14+d(4, 9), c15+d(5, 9)}=min{9+9, 8+9}=17(1→5)

　　d(0, 9)=min{c01+d(1, 9), c02+d(2, 9), c03+d(3, 9)}=min{4+17,2+15, 3+13}=16(0→3)

　　最后，得到最短路径为0→3→5→8→9，长度为16。

　　下面考虑多段图的最短路径问题的填表形式。用一个数组cost[n]作为存储子问题解的表格，cost[i]表示从顶点i到终点n-1的最短路径，数组path[n]存储状态，

path[i]表示从顶点i到终点n-1的路径上顶点i的下一个顶点。则：

　　cost[i]=min{cij+cost[j]} (i≤j≤n且顶点j是顶点i的邻接点)   （式1）

　　path[i]=使cij+cost[j]最小的j     （式2）

　　伪算法如下：

　　1．初始化：数组cost[n]初始化，数组path[n]初始化；

　　2．for (i=n-2; i>=0; i--)

　　　　2.1 对顶点i的每一个邻接点j，根据式8.5计算cost[i];

　　　　2.2 根据式8.6计算path[i];

　　3．输出最短路径长度cost[0];

　　4. 输出最短路径经过的顶点：

　　　　4.1 i=0

　　　　4.2 循环直到path[i]=n-1

　　　　　　4.2.1 输出path[i];

　　　　　　4.2.2 i=path[i];

　　根据上面伪算法，列出每步的步骤：

　　初始化：path[0-9]=[-1,-1,-1,-1,-1,-1,-1,-1,-1];cost[0-9]=[0,0,0,0,0,0,0,0,0];

　　根据式子计算得到：

　　i=8时,cost[8]=3,path[8]=9

　　i=7时,cost[7]=7,path[7]=9

　　i=6时,cost[6]=8,path[6]=8

　　i=5时,cost[5]=9,path[5]=8

　　i=4时,cost[4]=12,path[4]=8

　　i=3时,cost[3]=13,path[3]=5

　　i=2时,cost[2]=16,path[2]=5

　　i=1时,cost[1]=17,path[1]=5

　　i=0时,cost[0]=16,path[0]=3

　　所以，最短路径应该为0-->3-->5-->8-->9，值为cost[0]的值16。

时间复杂度：第一部分是初始化部分，其时间性能为O(n)；第二部分是依次计算各个顶点到终点的最短路径，由两层嵌套的循环组成，外层循环执行n-1次，内层循环对所有出边进行计算，并且在所有循环中，每条出边只计算一次。假定图的边数为m，则这部分的时间性能是O(m)；第三部分是输出最短路径经过的顶点，其时间性能是O(n)。所以，算法的时间复杂性为O(n+m)。

4.最低费用问题

　　一个商人穿过一个 N*N 的正方形的网格，去参加一个非常重要的商务活动。他要从网格的左上角进，右下角出。每穿越中间1个小方格，都要花费1个单位时间。商人必须在(2N-1)个单位时间穿越出去。而在经过中间的每个小方格时，都需要缴纳一定的费用。

这个商人期望在规定时间内用最少费用穿越出去。请问至少需要多少费用？

　　代码：

#include <iostream>
#include <cstdio>
using namespace std;
#include <cstdlib>
#define M 101
#define n 4
int f[M][M], a[M][M];
int main() 
{
    int max=5,min=1;
    int x_p,y_p;
    int m=n,u=n;
    int path[n+1][n+1][2];//用来存储(i,j)的前一个点坐标分别是[i][j][0]与[i][j][1]，n+1表示不使用0下标，用1~n与实际坐标保持一致
    for(int x = 1; x <= n; x++)
    {
    	 for(int y = 1; y <= n; y++) 
    	 {
            a[x][y]= rand() % (max - min) + min;
            if(x == 1) {f[x][y] = a[x][y] + f[x][y-1];}//初始化1行 
            if(y == 1) {f[x][y] = a[x][y] + f[x-1][y];}//初始化1列
         }
    } 
    for(int k1=1;k1<=n;k1++)
    {
    	for(int k2=1;k2<=n;k2++)
    	{
    		printf("%d ",a[k1][k2]);
    	}
    	 printf("\n");
    }
     printf("\n");
     printf("初始化\n");
     for(int t1=1;t1<=n;t1++)
    {
    	for(int t2=1;t2<=n;t2++)
    	{
    		printf("%d ",f[t1][t2]);
    	}
    	 printf("\n");
    }
    printf("\n");
    for(int i = 2; i <= n; i++)
    {
    	for(int j = 2; j <= n; j++) 
    	{
    		f[i][j] =((f[i-1][j]<f[i][j-1])?f[i-1][j]:f[i][j-1]) + a[i][j];//f[i][j]最小值由上一行或前一列得来 		
    		if(f[i-1][j]<f[i][j-1])
    		{
    			path[i][j][0]=i-1;
    			path[i][j][1]=j;
    		}else{
    			path[i][j][0]=i;
    			path[i][j][1]=j-1;
    		}
    	}
    }
   
    printf("最短路径为%d\n", f[n][n]);
    printf("存储最短路径的矩阵\n");
    for(int a = 1; a <= n; a++)
    {
    	 for(int b = 1; b <= n; b++) 
    	 {
            printf("%d ",f[a][b]);
    	 }
    	 printf("\n");
    }
    printf("最短路径的坐标逆序：");
    while(m>1&&u>1)//自底向上输出路径坐标
    {
    	 x_p=path[m][u][0];
         y_p=path[m][u][1];
         printf("(%d,", x_p);
         printf("%d)<---- ",y_p);
         m=x_p;
         u=y_p;
    }
    return 0;
}

　　

　　所以最后的路径应该为如下图:

 

 

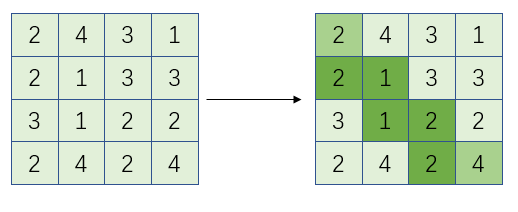
　　总结：动态规划法将待求解问题分解成若干个相互重叠的子问题，每个子问题对应决策过程的一个阶段，一般来说，子问题的重叠关系表现在对给定问题求解的递推关系（也就是动态规划函数）中，将子问题的解求解一次并填入表中，当需要再次求解此子问题时，可以通过查表获得该子问题的解而不用再次求解，从而避免了大量重复计算。

 

 

参考链接：https://www.cnblogs.com/xing901022/archive/2012/10/16/2726820.html

不足或错误之处，欢迎指正与评价!