条件概率与朴素贝叶斯
1.条件概率
条件概率是指事件A在事件B发生的条件下发生的概率。条件概率表示为：P（A|B），读作“A在B发生的条件下发生的概率”。若只有两个事件A，B，那么：
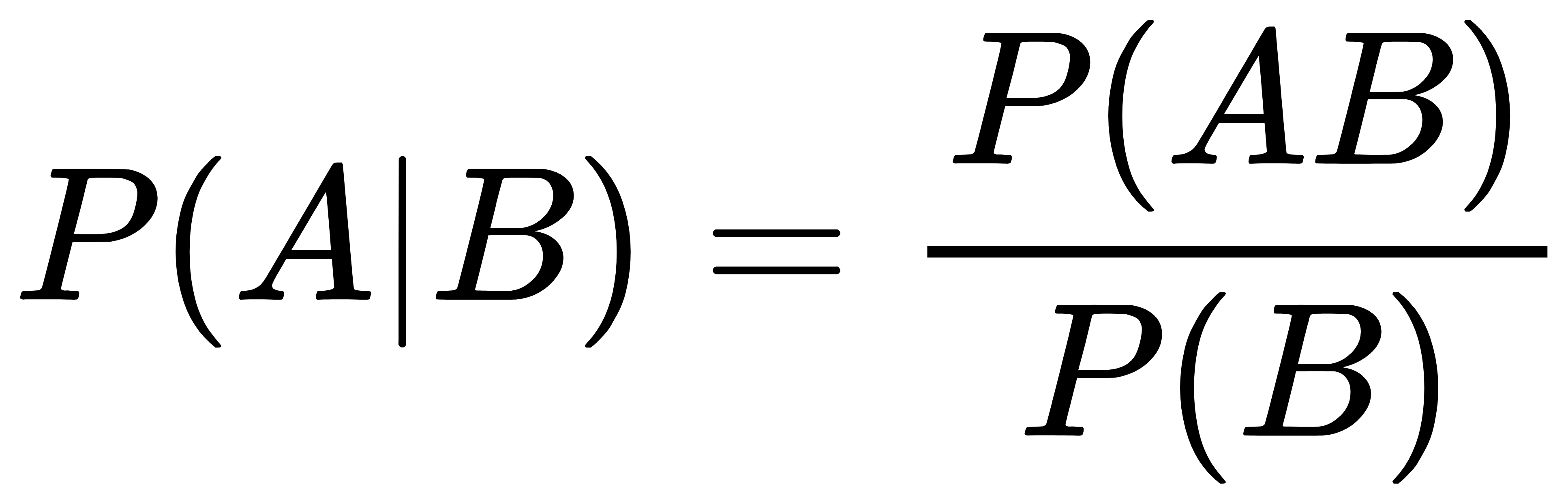
在上式中P(B)不能等于0，另外，如果A,B相互独立，有P(AB)=P(A)P(B)
2.全概率公式
全概率公式为概率论中的重要公式，它将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。如果事件B1、B2、B3…Bi构成一个完备事件组，即它们两两互不相容，其和为全集；并且P(Bi)大于0，则对任一复杂事件A有：
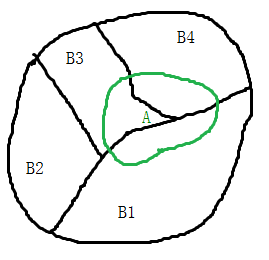
当直接计算P(A)较难时，可以用全概率公式展开。P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+…+P(A|Bi)P(Bi)。或者：
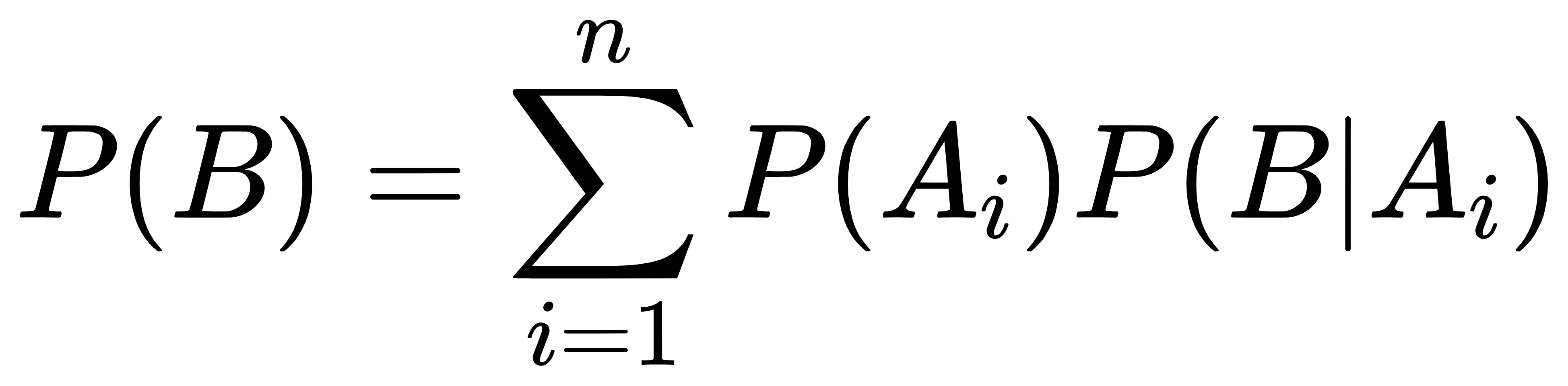
3.贝叶斯(Bayesian)定理
设B1，B2，…Bn…是一完备事件组，则对任一事件A，P（A）>0，有
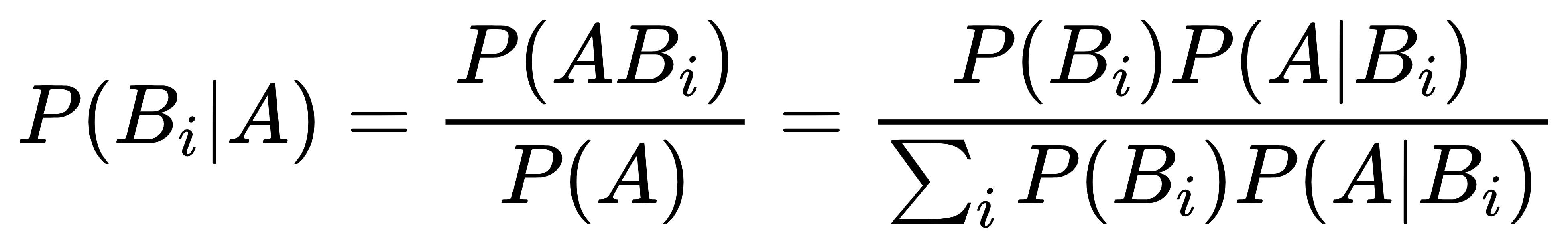
上式中P(Bi|A)为条件概率,P(ABi)为联合概率,P(A)为边缘概率或全概率。
下图为西瓜好坏的15个样本数据集。
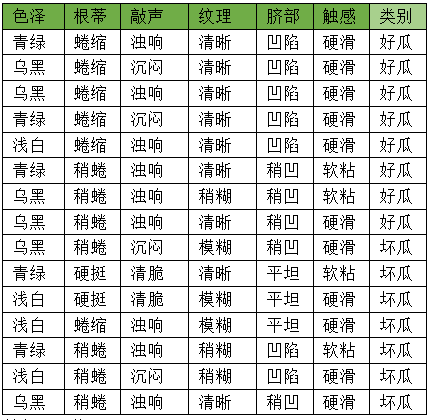
特征及取值：
色泽：青绿，乌黑，浅白
根蒂：蜷缩，稍缩，硬挺
敲声：浊响，沉闷，清脆
纹理：清晰，稍糊，模糊
脐部：凹陷，稍凹，平坦
触感：硬滑，软粘
我们现在挑选了一个色泽青绿、根蒂蜷缩、敲声沉闷、纹理清晰（这里只选四个特征），在该条件下，求该西瓜是好瓜的概率是多少？
我们其实要求P(好瓜|色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)，根据条件概率公式得到：
P(好瓜|色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)=P(好瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))/P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)。
我们现在条件概率公式分别计算得到
P(好瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))=1/15
P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)=1/15
P(好瓜|色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)=1
没错，根据此样本，条件概率公式得到的概率就是1。
为方便表示，现在假设挑选一个瓜为好瓜为事件A1，坏瓜为事件2,色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰分别为事件B1,B2,B3,B4。所以：
P(A1|B)=P(A1B)/P(B)，再根据贝叶斯公式得到：P(A1|B)=P(A1B)/P(B)= P(A1)P(B|A1)/P(B)=(8/15)*(1/8)/(1/15)=1
这里我们可以根据样本算一下P(A1B)并不等于P(A1)*P(B)，也就是特征与标签两者并不独立。
上面例子特征太多，现在假设只知道三个特征，纹理清晰，色泽青绿，如何使用朴素贝叶斯分类器求该西瓜是好瓜与坏瓜？其实就是求在此条件下，好瓜的概率大还是坏瓜的概率大。
那么通过条件概率可以求得西瓜在特定条件下好瓜的概率，为什么还要用贝叶斯公式来算。因为往往联合概率不知道，知道的是先验概率与后验概率,从而求已知后验概率的逆概率。比如，如下例子：
已知西瓜有好瓜与坏瓜，好瓜概率为8/15，坏瓜概率为7/15，好瓜里面纹理清晰的概率是7/8，坏瓜里面纹理清晰的概率是2/7。现在挑选一个纹理清晰的西瓜，求该瓜是好瓜的概率。
纹理清晰的后验概率：P(纹理清晰|好瓜)=7/8
先验概率：P(好瓜)=8/15
纹理清晰的后验概率：P(纹理清晰|坏瓜)=2/7
先验概率: P(坏瓜)=7/15
P(好瓜|纹理清晰)=P(好瓜,纹理清晰)/P(纹理清晰)
=P(纹理清晰|好瓜)P(好瓜)/P(纹理清晰)
= P(纹理清晰|好瓜)P(好瓜)/{ P(纹理清晰|好瓜)P(好瓜)+ P(纹理清晰|坏瓜)P(坏瓜)}
=(7/8)*(8/15)/{(7/8)*(8/15)+(2/7)*(7/15)}
=7/9
此时，1- P(好瓜|纹理清晰)=2/9或者再使用公式求得P(坏瓜|纹理清晰)
P(坏瓜|纹理清晰)= P(坏瓜,纹理清晰)/P(纹理清晰)
= P(纹理清晰|坏瓜)P(坏瓜)/P(纹理清晰)
=P(纹理清晰|坏瓜)P(坏瓜)/{ P(纹理清晰|好瓜)P(好瓜)+ P(纹理清晰|坏瓜)P(坏瓜)}
=(2/7)*(7/15)/ {(7/8)*(8/15)+(2/7)*(7/15)}
=2/9
所以根据贝叶斯分类器，选择概率大的一类，为好瓜。
4.朴素贝叶斯分类器例子
朴素贝叶斯分类器是以贝叶斯定理为基础的一类分类算法。贝叶斯分类器以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提。换言之，假设每个属性独立地对分类结果发生影响（事实上不一定是）。通过先验概率P(Bi)，计算后验概率P(Bi|A)。朴素贝叶斯是指对于假设模型的特征有强独立性，不考虑特征与特征之间的相关性(若独立性越强，使用其分类效果越好)。
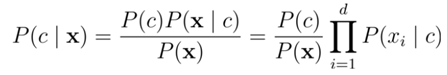
求概率时，由于分母相同，所以朴素贝叶斯判定准则有：
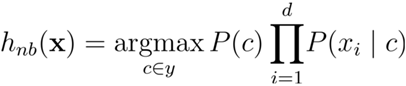
继续以上面四个特征例子为讲解：
P(好瓜|色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)=P(好瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))/P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)。
但是通过有限少量样本对于多个属性条件下的条件概率难以直接估计或是与真实差别太大。比如这里的P(好瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)) =P(好瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))/P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)。
分子又可以转换为P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰|好瓜)P(好瓜)。
由于我们假设各特征之间有强独立性。所以
P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰|好瓜)=P(色泽青绿|好瓜)P(根蒂蜷缩|好瓜)P(敲声沉闷|好瓜)P(纹理清晰|好瓜)
=(3/8)*(5/8)*(2/8)*(6/8) =0.044
P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)= P(色泽青绿)P(根蒂蜷缩)P(敲声沉闷)P(纹理清晰)
=(5/15)*(6/15)*(4/15)*(9/15)=0.0213
P(好瓜|色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)=0.044*(8/15)/ 0.0213
同理P(坏瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)) =P(坏瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))/P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)。
分子P(坏瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))=P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰|坏瓜)P(坏瓜)P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰|坏瓜)=P(色泽青绿|坏瓜)P(根蒂蜷缩|坏瓜)P(敲声沉闷|坏瓜)P(纹理清晰|坏瓜)=(2/7)*(1/7)*(2/7)*(2/7)=0.003
P(坏瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))=0.003*(7/15)/0.0213
显然P(好瓜|色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)> P(坏瓜,( 色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰))，所以贝叶斯分类器分类为好瓜。上式中其实不需要算分母，比较分子即可，并且仔细观察发现，这样算的概率可能大于1，而且我们计算P(色泽青绿，根蒂蜷缩，敲声沉闷，纹理清晰)是拆分P(色泽青绿)P(根蒂蜷缩)P(敲声沉闷)P(纹理清晰)来算的（本人是这样考虑的），肯定与真实值存在区别，因为他们并不一定相互独立。实际过程中只需要比较大小即可(朴素贝叶斯判定准则)！
5. 拉普拉斯平滑
在计算实例的概率时，如果某个量x，在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是0。这是不合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是0。为了解决这0概率事件问题，引入Laplace校准，它的思想非常简单，就是对每个类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面。
先验概率拉普拉斯修正：
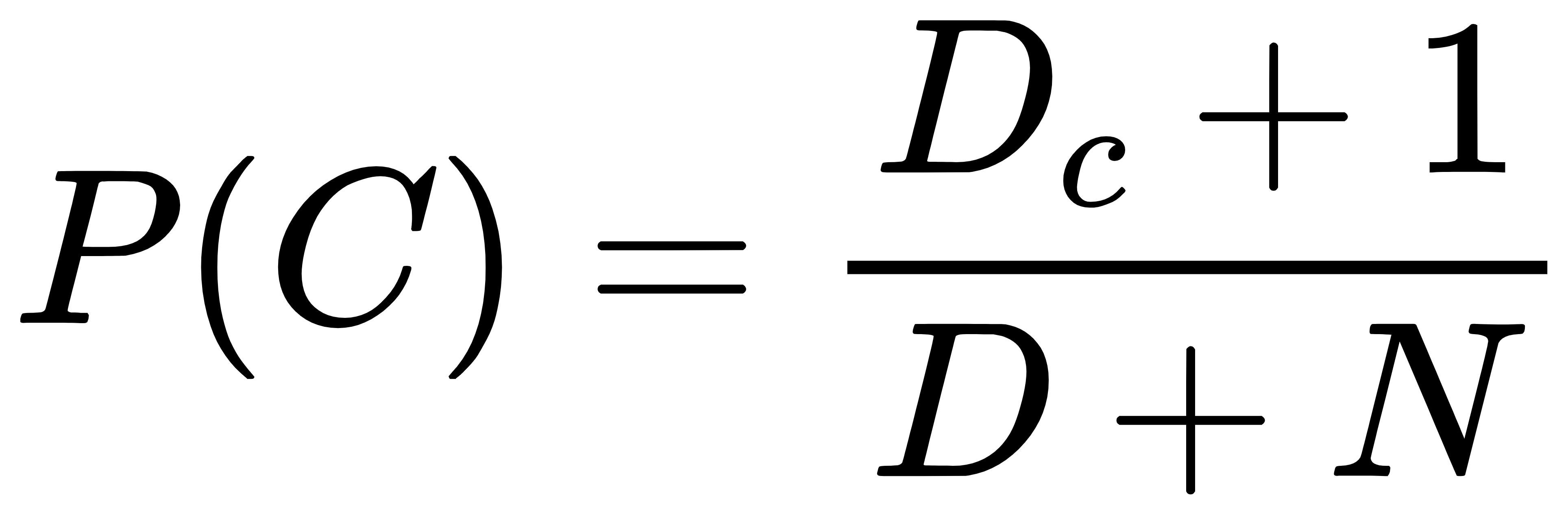
Dc表示训练集中，分类为 C的样本个数 ;D 表示训练集中样本中个数 ;N表示按照某属性分类的类别数。
类条件概率（似然）的拉普拉斯修正：
Si是分类为Ci类型的数据集样本个数；Sik是被分类成Ci类型的样本中，Xk的样本个数。
6. 代码实现
在python的scikit-learn库中包含了伯努利贝叶斯、多项式朴素贝叶斯、伯努利朴素贝叶斯分类器。这里使用纯python实现对西瓜好坏的分类。
import pandas as pd import numpy as np from functools import reduce
def readFile(path): df=pd.read_csv(path) return df if __name__=='__main__': #读取数据 df=readFile('西瓜数据.csv') #计算得到标签的类别 labelDataFrame=df.iloc[:,-1] col=df.shape[1]#列数,7 row=df.shape[0]#行数,15 labelArray=np.array(labelDataFrame) labelList=labelArray.tolist() labels=list(set(labelList))#['好瓜','坏瓜'] #测试数据 test1 = ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'] # test2=['浅白','蜷缩','浊响','模糊','平坦','硬滑','坏瓜'] classNum=[]#得到每个类的特征个数，用于后面计算类条件概率 for c in range(0,col-1): #0~5 colDF=df.iloc[:,c] colDFList=np.array(colDF).tolist() classList=list(set(colDFList)) classNum.append(len(classList)) # print(classNum)#[3, 3, 3, 3, 3, 2] # 利用朴素贝叶斯判定准则求各类别的概率 #采用拉普拉斯修正，计算各个类别的先验概率 PriorProbability={} CNum={}#{“好瓜”:7,"坏瓜":8} conditionalProbability={}#类条件概率 for label in labels: PriorProbability[label]=(labelList.count(label)+1)/(len(labelList)+2)#循环完后结果是{'好瓜': 8/17, '坏瓜': 9/17} CNum[label]=labelList.count(label) # print(CNum) #假设x1,x2...xn互相独立对结果产生影响的情况下，再计算拉普拉斯修正的各个类条件概率，根据判定准则不考虑分母，结果可能大于0的。 for label in labels: listConditional=[] i=0 for test in test1[:-1]: colClassNum=np.array(df.iloc[:,i]).tolist().count(test) # print(colClassNum) listConditional.append((colClassNum+1)/(CNum[label]+classNum[i])) i=i+1 conditionalProbability[label]=listConditional # print(conditionalProbability) # {'好瓜': [0.45, 0.63, 0.90, 0.36, 0.36, 1.2], '坏瓜': [0.5, 0.7, 1.0, 0.4, 0.4, 1.33]} #根据判定准则计算此情况下好瓜与坏瓜的概率（分子部分）大小 result={} for label in labels: # print(reduce(lambda x,y:x*y,conditionalProbability[label])) P_label=PriorProbability[label]*reduce(lambda x,y:x*y,conditionalProbability[label]) result[label]=P_label print(result)#{'好瓜': 0.019881170268679953, '坏瓜': 0.0316235294117647} keys, values = list(result.keys()),list(result.values()) finallyResult=keys[values.index(max(values))] print("在此种情况下:",test1[:-1],"朴素贝叶斯判定器根据六个特征判定该瓜为",finallyResult) print("实际结果:",test1[-1])
不足或错误之处，请提出与指正，谢谢!
