算法
目录
- 一、贪心算法
- 二、动态规划法
一、贪心算法
贪心算法是指,在对问题求解的时候,总是做出在当前看来是最好的选择,也就是说,不从整体最优上加以考虑,他做出的是在某种意义上的局部最优解。
因此,贪心算法并不能保证得到最优的解。参考第一章绪论的道路通行例子。但是也有一些解用贪心算法得出的是最优解。
1、贪心法例子
找零问题
假设商店保留需要找零n元钱,钱币的面额有:100元、50元、20元、5元、1元,如何找零使得所需钱币的数量最少?
基本思想: 尽可能先让大面值的钱币得到结果,然后往下一步考虑较小的面值
问题:结果存放在哪里?
解决:可以存放到另外一个辅助结构中。这里选择一个顺序表list。
时间复杂度O(nlogn)
空间复杂度O(n)

import time def get_time(fun): def wrapper(*args, **kwargs): st = time.time() re = fun(*args, **kwargs) print(time.time() - st) return re return wrapper @get_time def get_money(lst, target): lst.sort(reverse=True) i, result = 0, [0 for i in range(len(lst))] while i < len(lst): if target >= lst[i]: target -= lst[i] result[i] += 1 else: i += 1 return result @get_time def get_money1(lst, target): lst.sort(reverse=True) i, result = 0, [0 for i in range(len(lst))] while i < len(lst): result[i] = target // lst[i] target %= lst[i] i += 1 return result lst = [100, 50, 20, 5, 1] print(get_money(lst, 123)) print(get_money1(lst, 123))
这里注意get_money效率很低,当target的规模足够大的时候,需要花费很大量的时间来做减法操作。
背包问题
一个小偷在某个商店发现有n个商品,第i个商品价值vi元,重wi千克,他希望拿走的价值尽量高,但它的背包最多只能容纳W千克的东西。他应该如何选择商品?
0-1背包:对于一个商品,要么把它完整拿走,要么把它留下。
分数背包:一个商品,可以拿走其中一部分。
对于0-1背包和分数背包,贪心算法是否都能得到最优解?为什么?
0-1背包如果使用贪心法不能达到最优解。例如:
商品1:v1=60, w1=10
商品2:v2=100, w2=20
商品3:v3=120 w3=30
假设背包容量为50,如果按照贪心法来计算商品1的单位价值最高,应该先装它,其次是商品2,然后背包装不下商品3,结束。这样显然得到的并不是最优解。
但是如果是分数背包,却可以通过贪心法来得到最优解。因为可以装一部分,因此最后商品3可以能装多少装多,最后就装20重量的商品3。这显然是最优解。

def fractional_backpack(lst, w): lst.sort(lst, key=lambda x: x[0] / x[1], reverse=True) i = 0 money = 0 while i < len(lst): if w >= lst[i][1]: w -= lst[i][1] money += lst[i][0] else: money += w * lst[i][0] / lst[i][1] break i += 1 return money
拼接最大数字问题
有n个非负整数,将其按照字符串的方式拼接为一个整数,怎么拼接才可以得到的整数最大?

def get_str(lst): res = list(map(str, lst)) res.sort(reverse=True) return ''.join(res) print(get_str([32, 94, 128, 1286, 6, 71]))
活动选择问题
假设有n个活动,这些活动要占用同一片场地,而场地在某个时刻只能提供一个活动使用。
每个活动都有一个开始时间si和结束时间fi(题目中时间以整数表示),表示活动在[si, fi]区间占用场地。
安排哪些活动能够使该场地举办的活动的个数最多?

def activities_selection(lst, target_time): i = 0 lst.sort(key=lambda x: x[1]) p = target_time[0] res = [] while i < len(lst): start, end = lst[i][0], lst[i][1] if p <= start and target_time[1] >= end: p = end res.append(lst[i]) i += 1 return res print(activities_selection([(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)], (1, 16)))
二、动态规划
动态规划思想(DP)=递推式+重复子问题
1、钢条切割问题
现在有一段长度为n的钢条和上面的价格表,求切割钢条方案,使得总收益最大。

def get_list(price): max_price = [0, 1] i = 2 while i < len(price): j = i max_price.append(price[j]) prices = [] while 2 * j >= i: prices.append(max_price[j] + max_price[i - j]) j -= 1 max_price[i] = max(prices) i += 1 print(max_price) return max_price price = [None, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
2、最长公共子序列
子序列的概念
一个序列的子序列是在该序列中删去若干元素后得到的序列。注意跟子串的区别,子串是连续的,子序列可以是不连续的。
例如:'ABCD'和'BDF'都是'ABCDEFG'的子序列。
最长公共子序列(LCS)问题
问题描述:
给定两个序列X和Y,求X和Y长度最大的公共子序列。
例如: X='BDCABA' Y='ABCBDAB'
那么这两个字符串的最长公共子序列的长度是4,最长公共子序列是:BCBA。
算法求解:
动态规划求解的问题,一般有两个特征:1、最优子结构。2、重叠子问题。
最优子结构
现在假设X=(x1,x2,...,xn)和Y=(y1,y2,...,ym)是两个序列,那么将X和Y的最长公共子序列记为LCS(X,Y)。
分析:
如果要找出LCS(X,Y),也就是找到X和Y中最长的你哥哥公共子序列。首先要考虑的是X的最后一个元素和Y的最后一个元素。
- 如果xn=ym,也就是X的最后一个元素等于Y的的最后一个元素。那么LCS(X, Y)就是LCS(Xn-1,Ym-1)+1。因此现在的问题就是找出LCS(Xn-1,Ym-1)。由此可得,LCS(X-xn,Y-ym)问题是比LCS(X, Y)问题规模小一点的子问题。而LCS(Xn-1,Ym-1)得到的解就是最优解,因此,LCS(X, Y)=LCS(Xn-1,Ym-1)+1得到的肯定也是最优解。
- 如果xn!=xm。这里产生了两个子问题:LCS(Xn-1,Y)和LCS(Xn,Ym-1)两个问题。因为最后一个元素不相等,所以它不可能是公共的序列。LCS(Xn-1,Y)表示,最长公共序列在X(x1, x2,...xn-1)和Y(y1, y2,...,ym)中找。LCS(X,Ym-1)表示,最长公共序列在X(x1, x2,...xn)和Y(y1, y2,...,ym-1)中找。那么要找到最长的公共序列,就看这两个谁比较大。因此上面两个子问题最优解就是LCS=max{LCS(Xn-1,Y),LCS(X,Ym-1)}
重叠子问题
在上面的分析中,可知得出LCS(X, Y),必须要对
LCS(Xn-1,Ym-1),LCS(Xn-1,Y),LCS(X,Ym-1)三个子问题分别求解。而要对这三个问题求解的步骤也是一样,先比对最后一个元素。然后重复上面最优子结构的步骤,这样就会产生重叠子问题的现象。
举个例子:如果对LCS(Xn-1,Y)求解,当xn-1 != ym的时候,就需要对LCS(xn-2, Y)和LCS(xn-1, Yn-1)分别求解。这时会发现LCS(xn-1, Yn-1)这个子问题跟前面求LCS(X,Y)时,当xn=ym时求解的子问题是一样的。因此就会反生重叠。
那么,显然,如果有重叠子问题的性质,用递归来求解的话效率太低(重复计算了很多子问题)。这里所有子问题加起来的个数是指数级别的。
因此这里使用动态规划,不用再一一去计算那些重复的子问题。直接通过查找获得。
要解决这个问题,先写下最长公共子序列的递归式。
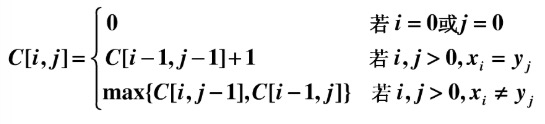
这里使用一个二维数组来记录公共子序列的长度。其中i是代表的是列,也就是X中的指针,j代表的是行,也就是Y中的指针。c[i][j]代表LCS(xi, yj)的长度,也就是序列X(x1,x2,...,xi)和序列Y(y1,y2,...,yj)的公共子序列长度的最大值。
def lcs_length(x, y):
m, n = len(x), len(y)
c = [[0 for j in range(n + 1)] for i in range(m + 1)] # 考虑空串情况,因此要多一个选项。
for i in range(1, m+1): # i是二维数组的列
for j in range(1, n+1): # j是二维数组的行
if x[i-1] == y[j-1]: # 这里i-1是x的下标,j-1是y的下标
c[i][j] = c[i - 1][j - 1] + 1
else:
c[i][j] = max(c[i - 1][j], c[i][j - 1])
print(c)
return c[m][n]

上面代码注意下标问题,因为c在存储的时候必须考虑空串的情况,并且它也是递推式的初始数据。例如:求X(x1)和Y(y1)的最大公共子序列的长度。如果x1=y1,显然L(x1, x2)=1,当x1!=y1,L(x1, x2)=0。如果给初始位置都赋值为0,显然上面的算法也是满足条件的。
但是,最后的结果是要求最长的子序列,并不是求它的长度,因此,这里我们除了保存序列的长度之外,还需要保存它的额外信息。
由上面的分析可知,最长序列的来源是三个子问题,那么这三个子问题中,当xi=yj的时候,才会加1。也就是说,当xi=yj的时候,LCS(xi, yj)才会发生变化,而变化的结果就是把最后一个字符加入到LCS(xi-1, yj-1)的结果中。因此,当xi=yj的时候,把那个字符信息保存起来。最后就能得到一个完整的字符串信息。
def lcs_length(x, y): m, n = len(x), len(y) c = [[0 for j in range(n + 1)] for i in range(m + 1)] b = [[0 for j in range(n + 1)] for i in range(m + 1)] # 1代表数据来源于左上角,2代表数据来源于上面,3代表数据来源于左边。 for i in range(1, m + 1): for j in range(1, n + 1): if x[i - 1] == y[j - 1]: #来源于左上方 c[i][j] = c[i - 1][j - 1] + 1 b[i][j] = 1 elif c[i - 1][j] < c[i][j - 1]: # 来源于左边,也就是左边的比较大,也就是行的前一个元素比较大。 c[i][j] = c[i][j - 1] b[i][j] = 3 else: #来源于右上方 c[i][j] = c[i - 1][j] b[i][j] = 2 # 回溯追踪字符位置,这里注意反转。 l = [] while m > 0 and n > 0: if b[m][n] == 1: # 来源于左上方 l.append(x[m - 1]) m, n = m - 1, n - 1 elif b[m][n] == 2: # 来源上方 m -= 1 else: # 来源于左方 n -= 1 return ''.join(reversed(l))




