字典和集合

目录

• 一、数据存储、检索和字典
• 二、字典的线性表实现
• 三、散列和散列表
• 四、集合
• 五、python的dict和set
• 六、二叉排序树和字典
• 七、平衡二叉树

一、数据存储、检索和字典

计算机的基本功能是存储和处理数据。

1、数据存储和检索

数据访问的基本方式基于存储位置，如果知道所需要的数据保存在哪里，那么只需要常量时间就可以得到它。

但是很多情况下，并不确定数据的存储位置。这时就需要查字典。而对于计算要找到数据的存储位置的操作就是检索。

概述

数据检索有两个方面的信息：

• 已经存储的数据集合。
• 用户检索时提供的信息。(也叫做关键码key)

字典就是基于关键码的数据存储与检索的数据结构。

字典操作和效率

实际中使用的字典分两类：

• 静态字典。在建立之后，这种字典的内容和结构都不再变化，主要操作只有检索。因此检索的效率很重要。
• 动态字典。在初始常见之后，这种字典的内容将一直处于动态变动当中。除了检索之外，还有插入，删除操作等。因此不仅要考虑检索的效率，还要考虑插入和删除的效率等。

对于动态字典，如果长期使用，在设计的时候就必须保证其新增不会随着操作的进行而恶化。

因为检索效率很重要，因此这里有一个关于检索效率的评价标准，称为平均检索长度(ASL)，它通常考虑的是在一次完整的检索过程中比较关键码的平均次数。

 

 ci和pi分别是第i项数据元素的检索长度和检索概率。如果字典中各个元素的检索概率相等，也就是说，如果pi=1/n，那么ASL=1/nΣci。

字典和索引

字典是两种功能的统一：

• 提供数据存储功能。
• 提供数据检索功能。

后一种功能也称为索引，其目的就是为检索服务。

做基于关键码的检索，就是要实现从关键码到数据存储位置的映射，而这种映射就是索引。

后面的讨论只要与检索有关，即可以用于实现字典，也可以用于实现索引。在用于实现字典时，关键码关联与实际数据，数据项保存在本字典的内部。在用于实现索引，它就只提供了从关键码到相应的数据项存储位置的映射，而实际数据存储在与这个索引相关的字典里。

2、字典实现的问题

注意：各种字典都不允许修改关键码，因为关键码用于确定其所在字典里存储的位置，以支持高效的检索。如果允许修改关键码，那么就会破坏字典数据结构的完整性。

字典元素：关联

一个数据项包括两部分：

• 与检索有关的关键码key。
• 实际数据value。

class Assoc:
    def __init__(self, key, value):
        self.key = key
        self.value = value
    
    def __lt__(self, other):
        return self.key < other.key
    
    def __le__(self, other):
        return self.key <= other.key
    
    def __str__(self):
        retrun 'Assocc({}, {})'.format(self.key, self.value)

这里主要介绍两种方法的字典实现，一种是线性表实现，一种是效率高的散列表实现。

二、字典的线性表实现

1、基本实现

可以将关键码和关联作为元素顺序存入线性表，形成关联的序列。
检索就是在线性表里查找具有特定关键码的数据项，数据项的插入和删除等都是普通的线性表操作。

检索用顺序查找。插入用append，删除可以使用pop()，但是必须先定位。当然也可以直接使用remove。

时间复杂度

• 插入O(1)
• 删除O(n)，主要是检索下标需要O(n)
• 检索O(n)。

优缺点

• 优点：实现简单，并且适用于任意关键码类型。
• 缺点:
• * 检索效率低。不适合频繁检索的字典。
• * 删除效率低。不适合频繁变动的字典。

2、有序线性表和二分法检索

如果关键码是一个有序集合，就可以使用二分法来进行检索。

二分发是一个重要检索技术，它的基本思想是按照比例逐步缩小要考虑的数据范围。操作过程如下:

• 初始时，考虑的元素区间是整个字典(一个顺序表)
• 取所考虑的元素范围里位置居中的那个数据项，比较该项的关键码与检索关键字，如果它们相等则检索结束。
• 如果检索的关键码大，就把范围修改为中间项之后的半区间，如果检索的关键码小，就把范围修改为中间项的前半区间。
• 如果在关注的范围里仍然后数据，就回到2步骤，否则检索失败。

def bisearch(lst, key):
    low, high = 0, len(lst)-1
    while low <= high:
        mid = (low+high)//2
        if key == lst[mid].key:
            return lst[mid].value
        elif key < lst[mid].key:
            high = mid -1
        else:
            low = mid +1        

class DicList:
    def __init__(self):
        self._elems = []

    def is_empty(self):
        return self._elems is None

    def num(self):
        return len(self._elems)

    def search(self, key):
        elems = self._elems
        dlen = self.num()
        low, high = 0, dlen - 1
        while low <= high:
            mid = low + (high - low) // 2
            if key == elems[mid].key:
                return mid, elems[mid].value
            elif key < elems[mid].key:
                high = mid - 1
            else:
                low = mid + 1
        return low

    def insert(self, key, value):
        sult = self.search(key)
        if isinstance(sult, tuple):
            self._elems[sult[0]].value = value
        else:
            self._elems.insert(sult, Assoc(key, value))

    def delete(self, key):
        sult = self.search(key)
        if isinstance(sult, tuple):
            i, value = sult
            self._elems.pop(i)
            return value
        raise KeyError(key)

    def values(self):
        for i in range(self.num()):
            yield self._elems[i].value

    def entries(self):
        for i in range(self.num()):
            yield self._elems[i].key, self._elems[i].value

算法分析

• 插入数据。因为要保证有序，所以是O(n)。
• 删除数据。也是O(n)。
• 检索数据。O(logn)。实际就是基于二叉树的查找过程。

优缺点

• 优点：检索速度快。比较适合静态字典。
• 缺点：
• * 插入速度和删除速度都比较慢。
• * 只能用于关键码能排序的字典，不适合实现很大的动态字典。

3、字典线性表的总结

字典也可以通过链表实现，但是链表的检索天然需要扫描整个表，因此，并没有什么优势。所以，实际中人们很少使用链表实现字典。

用线性表实现字典只能满足部分静态字典的需求，对于动态字典而言不太适合。因为它的插入和删除操作比较慢。

因此，人们开发了另外的结构来实现字典，主要分为两类：

• 基于散列思想的散列表
• 基于树形结构的数据存储和检索技术。

三、散列和散列表

1、散列的思想和应用

什么情况下基于关键码能最快的找到所需要的数据？那就是当关键码是数据的地址的时候(或者下标)。

但是一般而言，关键码可能不是整数，即是关键码是整数也不一定是下标的取值范围。比如：身份证号，它是国家身份信息的关键码，如果把它当做下标来索引的话，那么就需要建立一个10的18次方的表。显然，这是不合理的。

那么怎么办呢？

这时可以考虑通过一个计算把关键字映射到下标上。那么这样基于关键字的访问，就是基于下标的直接访问，会很快得到结果。

具体方法：

• 选定一个整数的下标范围(通常是0或1开始)，建立一个包括相应元素位置范围的顺序表。
• 选定一个从实际关键码到上面顺序表下标的映射h。
• 在需要存入关键码key的数据value时，将其存入表中第h(key)个位置。
• 遇到以key为关键码检索数据时，将其存入表中第h(key)个位置。

这个h函数就是散列函数，也称为哈希函数，它就是从可能的关键码集合到一个整数区间(下标区间)的映射。

散列思想的应用

散列思想是计算领域中机器重要的思想。所谓的散列一般而言，就是精心设计的方式，从一段可能很长的数据生成一段很短(固定长度)的信息串。

应用领域：

• 检查文件的完整性。
• 网页传输中的各种安全检查和正确检查。
• 各种安全协议。

将散列技术应用于数据存储和检索，就得到了散列表，实现散列表首先需要选择合适的散列函数。

散列技术：设计和性质

如果一个字典的关键码集合很小，例如关键码是0-19的整数，那么直接用它们作为下标就是最好的选择。

但是一般情况都不是这样的。一般关键码的集合都非常大，针对这种情况，所用的下标集合通常都远远小于关键码集合的规模。也就是说，在实现散列表时，通常都有|KEY|>=|INDEX|.

因此，散列函数h就是一个从大集合KEY到小集合INDEX的映射。这样必然会出现多个不同的关键码，通过h，映射到同一个下标的位置情况。如果出现这种情况，我们就说这里出现了冲突。这个时候key1和key2是h下的同义词。因此，在考虑散列表的实现时，必须考虑如何解决冲突的问题。

对于一个固定规模的散列表，表中元素越多，其出现冲突的可能性就越大。这里一个重要的概念是负载因子。

从这个公式中可知，负载因子越大，出现冲突的可能性就越大。这个时候，就需要扩大散列表的存储空间，增加容纳的元素，降低其负载因子，减少出现冲突的概率。不过负载因子越小，散列表中的空闲空间就越大，因此，这里需要注意权衡问题。

因此，要基于散列结束实现字典，必须解决两大问题：

• 散列函数的设计。
• 冲突的消解机制。

2、散列函数

散列还是将将关键码集合KEY映射到下标集合INDEX中。因此，分别为定义的散列函数的参数域(KEY)和值域(INDEX)，使得f(key)的值都落在合法的下标范围内。另外一方面，散列函数尽可能分散，因为它的实现可能影响出现冲突的概率。

例如：把所有关键码都映射到下标为0的函数。这样当然能满足要求，f(key)落在合法的下标范围内，但是这让冲突最大化，也就失去了散列的意义。

因此，散列函数的设计，最重要的考虑是尽可能减少冲突的可能性。

设计散列函数主要考虑以下几点：

• 函数应把关键码映射到值域INDEX中尽可能大的部分。如果有些下标没有映射到，这个位置就无法用到，造成存储浪费。
• 不同关键码的散列值在INDEX里均匀分布，有可能减少冲突。
• 函数的计算应该简单。使用散列表就是要提高效率，而计算散列表的开销显然是索引中的一部分。

基于以上的几点，人们提出了下面的几种散列函数的方法

基于整数关键码的若干散列方法

如果事前知道关键码的集合及其分布，就能设计出合适的散列函数，这样就能有效缩短整数的取值范围，甚至保证使用中不会出现冲突。

1>数字分析法

这种方法是在给定的关键码集合，分析所有关键码中各位数字的出现频率，从中选出分布情况较好的若干数字作为散列函数的值。

例子：下面图中的关键码集合

上面图中h1把关键码的百位和个位数字拼接起来，然后把9位十进制的关键码树映射到2位十进制数的下标值，那么这样只需要用一个包含100个元素的表存储字典数据即可，并且使用中很少出现冲突。如果用h2把关键码的百位数字映射到下标0-9的范围内，那么就可以用一个包含10个元素的表存储字典数据。这样，如果key只有图中的几个，那么就节省了很多的存储。

但是，只有在关键码已知的情况下，才能有效使用这种方法。然而，最常见的情况都是需要存储和使用的数据不能再设计字典之前确定的。

2>折叠法

这种方法是将比较长的关键码切分为几部分，然后通过某种运算将它们合并。

例如：用加法并舍弃进位，或者用二进制串运算等。

例子：假设关键码都是10位整数，这里考虑将其分为3位一部分，然后把得到的3位整数相加并去掉进位，最后得到的结果为散列函数的值。比如1456268793，计算1+456+268+793=1518，去掉进位，散列值为518。这样就能映射到[0,999]的关键码区间了。

3>中平法

这种方法是先求出关键码的平法，然后再取出中间的几位作为散列值。

从上面的例子可以看出，对于关键码，散列函数设计有两方面需要注意：

• 把较长的关键码映射到较小的区间。
• 尽可能消除关键码与映射值之间明显的规律性。

总之，散列函数的映射关系越乱越好，越不清晰越好。

常用的散列函数

1>除余法

适合整数关键码，具体做法是用key除以一个不大于散列表长度m的整数p，得到的余数作为散列地址。

一般会将m取值为2的某个幂值，这样是为了存储管理方便。然后把p取值为小于m的最大素数。例如：有长度为128的key。那么p的值就是127。下标就是key mod 127 + 1。

设计散列函数的一个基本思想是让得到的结果尽可能没有明显的规律，在采用除余法时，如果用偶数作为除数，就会出爱心偶数关键码映射到偶数散列值，奇数关键码映射到奇数散列值的情况，这种情况应该避免。

除余法还有一个缺点是相近的关键码将映射到相近的值。

2>基数转换法

适合整数或者字符串关键码。具体做法是，先考虑整数关键码。取一个正整数r，把关键码看做基数为r的数(也就是r进制的数)，将其转换为十进制或者二进制。通常r取素数减少其规律性。

例如：r=13。那么

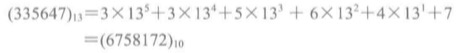
这时关键码的取值范围不合适，可以考虑用除余法，或者折叠法，或者删除几位数字等方法，将其归入所需要的下标范围。

如果遇到的是字符串，那么把一个字符看做一个整数(直接使用字符的编码值)，然后建议使用29或者31作为基数，通过基数转换法把字符串转换为整数，再用除余法，把结果归入散列表的下标范围。

def str_hash(s):
    '''
    将字符串转换为基数为29的整数。
    '''
    h1 = 0
    for c in s:
        h1 = h1 * 29 + ord(c)
    return h1

3、冲突的内消解技术：开地址技术

采用散列技术实现字典，出现冲突是必然的。因此，必须有解决冲突的方法：

• 内消解方法(在基本的存储区内部解决冲突问题)
• 外消解方法(在基本的存储区外解决问题)

处理冲突必须满足两方面的要求：

• 保证当前这次存入数据项的工作能正常完成。
• 保证字典的基本存储性质，在任何时候，从任何以前存入字典而后没有删除的关键码触发，都能找到对应的数据项。

开地址法和探查序列

开地址法的基本思路是：在准备插入数据并发现冲突时，设法在基本存储区里为需要插入的数据项另行安排一个位置。为此需要设计一种系统的并且易于计算的位置安排方式，称之为探查方式。

因此这里的关键就是设计一种探查方式。

定义一个递增序列D=d0,d1,d2....。d0=0。然后根据(h(key) +di) mod p求出hi，直到找到第一个hi上为空位的时候，把数据存入。这里的p是不超过表长度的数。

D的序列有多种设计方法。最简单的是D=0，1，2，3...，这种方法设计的探查方式称为线性探查。

也可以设计另外一个散列函数h2，令di=i*h2(key)，这种方法称为双散列探查。

开地址法例子

假设关键码为整数，存储数据表的长度是13，因此它的下标范围是0-12。
散列函数采用除余法h(key) = key mod 13。

KEY={18, 73, 10, 5, 68, 99, 22, 32, 46, 58, 25}

然后根据h(key)得出:

 

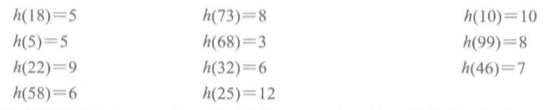
先考虑线性探查法：

• 前三个数据没有冲突。直接插入。
• h(5)=5，跟h(18)=5冲突，这个时候下标为5的位置已经有关键码为18的元素了。因此就要另外为它安排位置。
• 根据线性探查规则，((h(key)) + di) mod p求出第一个有空位的下标。
• 当di=0时。(5+0) mod 13 =5，不符合。di=1时，(5+1)mod 13 =6。此时下标为6的位置没有数据，然后插入。
• 然后h(68)直接插入
• h(99)冲突，找到位置9,然后插入。
• h(22)冲突，找到位置11，然后插入。
• h(32)=6，前面h(5)的时候已经把元素插入了下标为6的位置上，因此这里需要再次利用线性探查处理冲突。
• 当di=0时，(6+0) mod 13 =6，不符合，(6+1)mod 13 = 7。符合，然后直接插入元素。
• h(46)=7的时候，出现冲突。当di = 0时,(7+0)mod 13 = 7,不符合。di=1时，(7+1)mod 13 =8,不符合。di=2时，(7+2)mod 13 =9,不符合。di=3时，(7+3)mod 13 = 10，不符合。di=4时，(7+4)mod 13 = 11。不符合，di=5时，(7+5)mod 13 = 12，符合条件，然后插入。
• h(58)冲突，根据探查，找到位置0。然后插入
• h(25)冲突，根据探查，找到位置1，然后插入。
• 最后得到的散列表应该是这样的：[58,25,0,68,0,18,5,32,73,99,10,22,46]

从这个过程中可以看出，随着表的数据增加，产生冲突的可能性不断增长，使得探查序列变得越来越长，情况变得越来越糟糕，字典的操作的效率大大降低。

现在考虑双散列探查。h2(key) = key mod 5 +1。

• 前面三项没有冲突直接插入。
• h(5)=5冲突。i=0 时，d0=0，(5+0)%13=5，冲突。i=1时，d1=1*h2(5)=5%5+1=1,(5+1)%13=6，不冲突，存入。
• h(68)没冲突存入。
• h(99)=8冲突。i=0时，d0=0，(99+0)%13=8，冲突，i=1时，d1=1*h2(99)=99%5+1=5，(8+5)%13=0，bu 不冲突，存入。
• h(22)不冲突，存入。
• h(32)=6，冲突。i=0时，d0= 0，(32+0)%13=6，冲突。i=1时，d1=1*h2(32) = (32)%5+1=3,(6+3)%13=9,冲突。i=2时，d2=2\*h2(32) = 2\*3=6,(6+6)%13=12，不冲突，存入。
• h(46)不冲突，存入
• h(58)=6，冲突，探查后得到位置11，存入。
• h(25)=12，冲突。探查后得到位置1，存入。
• 最后得到的散列表位置，如下图。

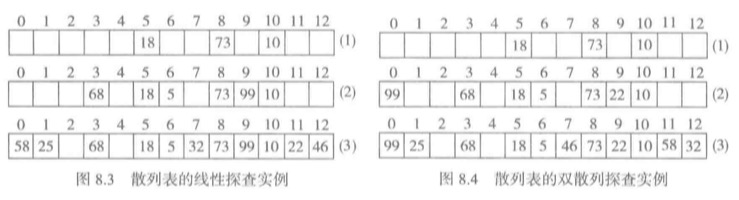
在双散列探查的过程中，检查的位置以不同方式跳跃。这种情况有可能减少关键码堆积的发送，但是随着表中元素的增加，冲突越来越严重的情况不会改变。

检索和删除

检索操作：

• 调用散列函数，求出key对应的散列地址。
• 检查对应的存储位置，如果没有数据，代表这个散列表里不存在对应的关键码，检索操作失败。
• 如果有数据，比较key与保存在该位置的关键码，如果匹配，检索成功，并结束。
• 如果不匹配，使用探查序列找到下一个地址，并回到步骤2。

可见，为判定找不到元素，还需要为单元的无值状态确定一种表示方式。

删除操作:

• 通过检索找到关键码。
• 删除元素。

利用开地址法的删除有个问题，被删除的数据有可能处于其他元素的探索路径上，如果简单把这个元素删除，可能就切断了其他元素的探索路径，从而导致那些元素‘失联’。

解决方法是:不在删除的元素位置存入空位标识，而是存入一个特殊标记。在执行检索操作的时候，把它看做元素继续向下探查，在执行插入操作的时候，把它看做空位，插入元素。

4、外消解技术

溢出区方法

人们提出的一种技术另外设置一个溢出存储区。当插入关键码的散列位置没有数据时，就直接插入，如果发生冲突就把对应的数据和关键码一起存入溢出区。数据在溢出区里顺序排列，对应的检索和删除操作也是先找到散列位置，如果那里有数据但是关键码不匹配，就转到溢出区顺序检索，直到找到要找的关键码，或者确定相应的数据不存在。

这种方法如果冲突项很少，溢出区的实际数据非常少，效果还不错，但是随着溢出区中的数据增多，字典的性能将趋向线性。

桶散列

另外一种做法是数据项不存在散列表的基本存储区，而是另外存放。只在散列表中保存对数据项的引用。这种设计称为桶散列，下面是桶散列的一种最简单的设计，拉链法。

在桶散列技术里，散列表的每个元素只是一个引用域，引用着一个保存实际数据的存储桶。

在拉链法中一个存储桶就是一个链接的结点表，字典中的数据项并不保存在散列表的主存储区，而是保存在对应结点表中的结点里。假设KEYS={18, 73, 10, 5, 68, 93, 24, 32, 46, 58, 25}，那么保存方式就是如下图格式保存。

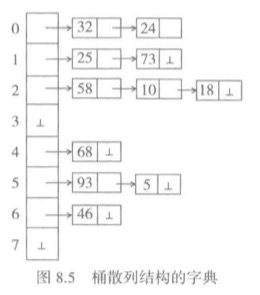
采用这种方式，可以允许任意的负载因子。

采用这种结构的操作，

• 插入操作：需要先找到关键码的散列位置，然后再执行插入，最简单的方式是把新数据插入到连接表的最前端，如果不允许出现重复关键码，就必须检查整个链表。
• 删除操作：找到关键码的散列位置，然后根据key找打对应的链表位置，删除。
• 检索操作：找到关键码的散列位置，然后根据key找到链表位置。

5、散列表的性质

扩大存储区，用空间交换时间

首先，可以看到，无论采用哪种技术，随着元素的增加，散列表的负载因子越大，出现冲突的可能性就越大。

如果采用开地址法，表中的数据增加最终将导致存储区溢出，而采用溢出区方法，溢出区越来越大，检索效率就越来越趋于线性。采用拉链法，负载因子增大就表现为链的平均长度增加。

因此，我们必须考虑，当负载因子达到一定的程度是，扩大散列表的基本存储表。

现在有一个问题，存储区扩大后，不能简单把元素直接拷贝到新的存储区，而是要把字典里已有的数据项重新散列到新的存储区。两者不一样的地方是，前者处理冲突是基于原来的基本存储表的下标范围。后者处理冲突是基于新的基本存储表的下标范围。如果更换了新表，而不使用新的下标范围，那么就会出现找错元素的情况。

由此，可见，扩大存储要付出重新分配存储区和再散列装入数据的代价。

对于散列表，只需要扩大存储，就能从概率上提高字典的操作效率。这是明显的用空间换取时间(计算机科学技术领域的一条基本原理)。

负载因子和操作效率

人们长时间的经验和研究得出一个结论，采用内部消解技术，当负载因子a<=0.7~0.75的时候，散列表的平均检索长度接近于常数。

采用桶散列技术，负载因子可以容忍任意大，但是当它不断变大的时候，检索时间也趋于线性。

因此，在设计散列表的时候要注意：

• 实际存入字典的数据的散列函数值要分布均匀。
• 字典散列的负载因子不能太高(最好在0.7以下)。

有了这些条件之后，是散列表字典的检索、插入和删除操作的时间开销就可以看作是常量时间。

虽然散列表的效率比较高效，但是有一些情况必须知道：

• 其常量操作是平均代价，并不是每次操作的实际代价。
• 关键码冲突，可能导致操作代价增加，并且这种情况不能预知。
• 当负载因子不断增大的时候，需要更换存储区，这会导致一次很高代价的插入操作，而且这种情况也不能预知。
• 字典内部数据项的排列顺序无法预知，也没有保证。比如：散列函数设计不好，导致散列值集中在一段区域，这样就会导致非常长的探查序列，从而使字典低效。
• 长期使用内消机制的字典，会产生很多的已删除元素序列，影响很多的操作。

解决方法：

• 给用户提供检查负载因子和扩大散列表存储区的操作，这样，用户就可以在一段效率要求高的计算之前，根据需要先设定足够大的存储。
• 对于开地址散列表，记录或检查被删除项的量或者比例，在一定情况下自动整理。最简单的方法是分配一块存储区，把散列表里的有效数据重新散列到新区。这种方法可以消去开地址散列表里所有已经删除项的空位。

四、集合

1、集合的概念、运算和抽象数据类型

一个集合就是一些个体的汇集。如果集合S有个体e，就说e是S的一个元素。

描述集合的方法：

• 外延表示，只能描述有穷集合，写法是{}。例如：{1,2,3}
• 内涵表示，可以描述任意集合，写法是{e|p}。例如：{x|x是自然数且没有除1和其自身之外的因子}

一个集合中的元素称为集合的基数，或者集合的大小。

两个集合S和T相等，那么他们包含同样的元素。

还有一种重要关系是子集关系，如果集合S中所有的元素都是集合T中的元素，那么S就是T的子集。如果S是T的子集，但是S!=T，那么S是T的真子集。

集合运算

1>求并集运算

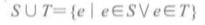
例如：S={1,2} T={3, 4}。S ∪ T={1,2,3,4}

2>求交集运算

例如：S={1,2} T={2,3}。S ∩ T ={2}

3>求差集运算

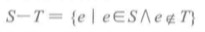
例如：S={1,2} T={2,3}。S - T ={1}。T -S ={3}

抽象数据类型

2、集合的实现

集合的实现类似于字典的实现，只不过是没有关联的数据。因此，前面所有实现字典的技术都可用于实现集合。

class LSet:
    '''
    采用顺序表实现的集合
    '''
    def __init__(self):
        self._elems = []

    def length(self):
        '''
        O(1)
        '''
        return len(self._elems)

    def elems(self):
        for i in self._elems:
            yield i

    def __str__(self):
        r = ''
        for i in self.elems():
            r += str(i) + ', '
        return r

    def is_empty(self):
        '''
        O(1)
        '''
        return self._elems is None

    def member(self, elem):
        '''
        元素elem是否在集合里.O(n)，列表in需要遍历
        '''
        return elem in self._elems

    def insert(self, elem):
        '''
        插入元素 O(n)
        '''
        if elem not in self._elems:
            self._elems.append(elem)

    def delete(self, elem):
        '''
        删除元素，先检索到位置，再删除。也可以直接使用remove()直接删除。O(n)
        '''
        for i in range(len(self._elems)):
            if elem == self._elems[i]:
                self._elems.pop(i)
                return
        raise KeyError('LSet Delete Error, Not elem')

    def intersection(self, oset):
        '''
        交集，结果生成一个新的集合。O(m*n)
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, intersection')
        new_set = LSet()
        for i in self.elems():
            for j in oset.elems():
                if i == j:
                    new_set.insert(i)
        return new_set

    def union(self, oset):
        '''
        并集，O(m*n)
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, union')
        new_set = LSet()
        for i in self.elems():
            new_set.insert(i)
        for j in oset.elems():
            if not new_set.member(j):
                new_set.insert(j)
        return new_set

    def different(self, oset):
        '''
        差集O(n*m)
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, union')
        new_set = LSet()
        for i in self.elems():
            if not oset.member(i):
                new_set.insert(i)
        return new_set

    def subset(self, oset):
        '''
        是否为oset的子集。
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, union')
        count = 0
        for i in self.elems():
            if oset.member(i):
                count += 1
        return count == len(self._elems)

这里插入元素时需要保证元素的唯一性，先检查它是否在集合里面。如果不在集合里面，再插入元素。删除元素的时候，直接找到第一个元素的下标，删除。

如果不需要保证唯一性，那么可以直接把元素插入集合中，当删除的时候，检查整个表，把所有跟元素相同的下标检索出来，然后再删除。

用线性表实现集合，技术比较简单，但是效率低下。

class LSet1(LSet):
    def member(self, elem):
        '''
        用二分法判断元素，O(logn)
        '''
        low, high = 0, len(self._elems) - 1
        while low <= high:
            mid = low + (high - low) // 2
            if elem == self._elems[mid]:
                return True
            elif elem < self._elems[mid]:
                high = mid - 1
            else:
                low = mid + 1
        return False

    def search(self, elem):
        '''
        用二分法检索元素位置，O(logn)
        '''
        low, high = 0, len(self._elems) - 1
        while low <= high:
            mid = low + (high - low) // 2
            if elem == self._elems[mid]:
                return mid
            elif elem < self._elems[mid]:
                high = mid - 1
            else:
                low = mid + 1
        return low

    def insert(self, elem):
        '''
        因为使用二分法判断，因此插入元素的时候必须保持元素有序，因此要插入固定的位置。O(n)
        '''
        if self.member(elem):
            return
        self._elems.insert(self.search(elem), elem)

    def delete(self, elem):
        '''
        先用二分找到位置，再pop()删除，因为要移动元素，因此需要O(n)
        '''
        if not self.member(elem):
            raise KeyError('LSet Delete Error, Not elem')
        self._elems.pop(self.search(elem))

    def intersection(self, oset):
        '''
        求并集。O(m+n)
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, intersection')
        i, j = 0, 0
        new_set = LSet1()
        while i < len(self._elems) and j < oset.length():
            if self._elems[i] < oset.get_elem(j):
                i += 1
            elif self._elems[i] > oset.get_elem(j):
                j += 1
            else:
                new_set.insert(self._elems[i])  #如果不必要保证集合有序，可以使用[]保存数据，用append添加，效率会高一些。
                i += 1
                j += 1
        return new_set

    def union(self, oset):
        '''
        求并集。O(m+n)
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, union')
        i, j = 0, 0
        new_set = LSet1()
        while i < len(self._elems) and j < oset.length():
            if self._elems[i] < oset.get_elem(j):
                new_set.insert(self._elems[i])
                i += 1
            elif self._elems[i] > oset.get_elem(j):
                new_set.insert(oset.get_elem(j))
                j += 1
            else:
                new_set.insert(self._elems[i])
                i += 1
                j += 1
        while i < len(self._elems):
            new_set.insert(self._elems[i])
            i += 1
        while j < oset.length():
            new_set.insert(oset.get_elem(j))
            j += 1
        return new_set

    def different(self, oset):
        '''
        求差集O(m+n)。
        '''
        if not isinstance(oset, LSet):
            raise TypeError('OsetTypeValue, different')
        i, j = 0, 0
        new_set = LSet1()
        while i < len(self._elems) and j < oset.length():
            if self._elems[i] < oset.get_elem(j):
                new_set.insert(self._elems[i])
                i += 1
            elif self._elems[i] > oset.get_elem(j):
                j += 1
            else:
                i += 1
                j += 1
        while i < len(self._elems):
            new_set.insert(self._elems[i])
            i += 1
        return new_set

这个实现一个明显的改善是检索时间变短了，集合称为了有序集合，因此在处理并集交集和差集的时候，有了更高效的方式。

class HSet:

    '''
    散列函数使用除余法和基数转换法。解决冲突使用内消解技术的开地址法。
    '''
    @staticmethod
    def prime(n):
    '''
    判断整数n是不是素数，用来得出p，也就是小于散列表长度的最大素数。
    '''
        if n == 1:
            return False
        t = int(math.sqrt(n) + 1)
        for i in range(2, t):
            if n % i == 0:
                return False
        return True

    @staticmethod
    def set_hash(key):
    '''
    将字符串转化成31进制的整数
    '''
        h1 = 0
        for i in key:
            h1 = 31 * h1 + ord(i)
        return h1

    def __init__(self, length=8):
        self._elems = [None] * length
        self._length = length  # 哈希表的长度
        self._prime = 7  # self._length的初始最大素数为7
        self._elelength = 0  # 哈希表中实际的元素个数

    def get_max_prime(self):
        '''
        得到不大于self._length的最大素数
        '''
        for i in range(self.hllength(), -1, -1):
            if HSet.prime(i):
                self._prime = i
                return self._prime
        raise ValueError('get_max_prime error, prime is too small')

    @property
    def loadfac(self):
        '''
        得到散列表的负载因子
        '''
        return round(self._elelength / self._length, 1)  # 保留一位小数

    def is_empty(self):
        '''
        判断是否为空，需要判断list里面的元素既不能是None，也不能是False，如果是None，代表空位，从未插入过元素。如果是None，代表空位，以前有元素，但是后来被删除了。O(n)
        '''
        for i in range(self._length):
            if self._elems[i] is not None and self._elems[i] is not False:
                return False
        return True


    def hllength(self):
        '''
        获得散列表的容量。
        '''
        return self._length


    def elelength(self):
        '''
        获得散列表的元素个数。
        '''
        return self._elelength

    def member(self, elem):
        '''
        判断元素是否在集合里
        '''
        index = self.search_index(elem)
        if self._elems[index] == elem:
            return True
        return False


    def get_insert_index(self, key):
        '''
        通过散列函数的映射查找要插入key的下标。
        '''
        if isinstance(key, str):
                # 如果key是字符串，先用基数转换法将其转换为整数
            int_key = HSet.set_hash(key)
        else:
            int_key = key
        f_index = int_key % self._prime
        
        # 这里探查序列使用的是双散列函数的序列
        for i in range(0, self._length):
            d = i * (int_key % 5 + 1)
            index = (f_index + d) % self._prime
            if self._elems[index] is None or self._elems[index] is False or self._elems[index] is key:
                return index
        raise ValueError('Explore_index Error,change hash list')


    def search_index(self, key):
        '''
        通过散列函数的映射查找key是否存在，如果存在返回下标，不存在返回False
        '''
        if isinstance(key, str):
            int_key = HSet.set_hash(key)
        else:
            int_key = key
        f_index = int_key % self._prime
        for i in range(0, self._length):
            d = i * (int_key % 5 + 1)
            index = (f_index + d) % self._prime
            if self._elems[index] == key:
                return index
            elif self._elems[index] is None:
                return False
        raise ValueError('Serach_index Error,change hash list')


    def extend(self):
        '''
        扩大哈希表的容量。必须重新将原散列表的key都散列到新的表中，因此这是个低效操作。
        '''
        self._length *= 4
        old_elems = self._elems
        self._elems = [None] * self._length
        self._elelength = 0
        self.get_max_prime()
        for i in range(len(old_elems)):
            if old_elems[i] is not None and old_elems[i] is not False:
                self.insert(old_elems[i])
        old_elems.clear()


    def entries(self):
        '''
        遍历集合元素
        '''
        elems = self._elems
        for i in range(self._length):
            if (elems[i] is not None) and (elems[i] is not False):
                yield elems[i]

    def insert(self, elem):
        '''
        集合里面插入元素
        '''
        # 当负载因子大于0.7的时候就扩大哈希表的容量
        if self.loadfac >= 0.7:
            self.extend()  # 扩大哈希表的容量
        index = self.get_insert_index(elem)
        if self._elems[index] == elem:
            return
        else:
            self._elems[index] = elem
        self._elelength += 1  # 实际元素长度加1，保证数据不变式。

    def delete(self, elem):
        '''
        删除元素，将其位置设置为False，保证不断开其他元素的探寻。
        '''
        index = self.search_index(elem)
        if index and self._elems[index] == elem:
            self._elems[index] = False
        else:
            raise KeyError('Delete Error, not exist key')
        self._elelength -= 1

    def intersection(self, oset):
        '''
        交集，O(m+n)
        '''
        if not isinstance(oset, HSet):
            raise TypeError('HsetTypeValue, intersection')
        new_set = HSet()
        for elem in self.entries():
            if oset.member(elem):
                new_set.insert(elem)
        return new_set

    def union(self, oset):
        '''
        并集，O(m+n)
        '''
        if not isinstance(oset, HSet):
            raise TypeError('HsetTypeValue, union')
        new_set = HSet()
        for elem in self.entries():
            new_set.insert(elem)
        for elem in oset.entries():
            new_set.insert(elem)
        return new_set

    def different(self, oset):
        '''
        差集，O(m+n)
        '''
        if not isinstance(oset, HSet):
            raise TypeError('HsetTypeValue, different')
        new_set = HSet()
        for elem in self.entries():
            if not oset.member(elem):
                new_set.insert(elem)
        return new_set

3、特殊实现技术：位向量实现

一个元素是否属于集合是一个二值判断，因此，人们提出了一种专门的集合实现技术：集合的位向量表示。具体方法：

• 假设U包含n个元素，给每个元素确定一个编号作为该元素的下标。
• 对任何一个要考虑的集合S，S是U的子集，用一个n位的二进制序列vs表示它，如果U里面的任何元素e，如果e在S里，那么vs对应于e的下标的二进制位取值1，否则取值为0。

例子：假设U={a,b,c,d,e,f,g,h,i,j}，包含10个元素，按照字母分别对应下标0，1，2，...,9。这样U的任何子集都能用一个10位的位向量表示：{}用0000000000表示。U用1111111111表示。s1={a,b,d}用1101000000表示。

位向量的集合操作都可以通过位运算来实现。

五、python的dict和set

python的字典和两个集合(set和forzenset)类型都是基于散列表技术实现的数据结构，采用内消解技术解决冲突。下面是dict的一些细节:

• dict采用散列表技术实现，其元素是key-value对，关键码可以是任何不变对象，值可以是任何对象。
• 在创建空字典或者很小的字典时，初始分配的存储区为8个元素。
• dict对象在负载因子超过2/3时自动更换更大的存储区，并把保存的内容重新散列到新存储区内。如果当前字典对象不太大，就4倍原散列表，如果超过50000，就2倍原散列表。

集合情况与此类似。只不过frozenset是不变对象，一旦建立之后就不会动态变化。

python规定dict的关键码，以及set和frozenset的元素都只能是不变的对象，是为了保证散列的完整性。

在python的标准函数中有一个hash函数，它的功能就是按照特定的方式计算参数的散列值，对一个对象调用hash函数，它或者返回一个整数，或者抛出一个参数异常，表示本函数对该对象无定义。

在dict和set等类型的实现中，python都是用这个hash函数计算关键码的散列值。

对于各种内置的不变类型，hash函数都有定义，包括内置的不变组合类型，例如：str，tuple，frozenset等。这个函数的定义还保证，当a==b时，两个对象的hash值也相同。

当程序代用hash函数时，解释器将到参数所属的类下面找__hash__方法。如果有这个方法，就是有定义。如果没有，就是无定义。

因此，如果希望自己自定义的对象也能作为dict或set等的关键码，就应该为这个类定义一个__hash__方法，当然，该类应该是不可变的对象，只支持构造和解析操作，不支持变动操作。

六、二叉排序树和字典

总结一下前面实现字典功能的三种方式：

• 基于简单的线性表实现，结构简单，容易实现，但是效率低下。
• 基于排序的顺序表实现，检索效率提高，但是插入和删除效率仍然很低，并且这种实现只适合关键码存在某种序的情况。
• 散列表实现。操作效率高，对关键码类型没有特殊要求(不变类型)。但是基于散列的字典没有确定性的效率保证，不适合用于对效率有严格要求的环境。另外，散列表不存在遍历元素的明确顺序。

这两种结构都是把字典存储在一个连续的存储块中，管理比较方便。但如果字典需要很大，就需要很大块的连续存储，动态修改不太方便，也难以实现非常巨大的字典。

为了更高支持存储内容的动态变化，应该考虑采用链接结构。此外，采用链接结构也很容易构造出巨型字典。

使用树形结构来实现字典的链接结构：

• 使用链接方式实现，比较容易处理元素的动态插入/删除问题(不需要移动元素)。
• 在树形结构里面，从根到任意结点的平均路径长度可以小到结点个数的对数，因此能够实现高效的操作。
• 支持高效的结构调整，保证长期工作的系统仍能维持良好的性能。(对于开地址法解决冲突的散列表而言不行)
• 支持大型字典的典型需要，比如数据库系统等实现。
• 尽可能很好地利用计算机系统的存储结构，比如，很好的利用内存和外村，以及硬件缓存等多层次存储结构。
• 用于大型数据集合建立索引，提高各种复杂查询效率。

下面主要是基于二叉树来实现字典，这里要注意二叉的的一个特点:

• 如果树结构比较好，那么最长路径的长度与树中结点个数呈对数关系。
• 如果树结构畸形，那么最长路径的长度与结点个数呈线性关系。

1、二叉排序树

二叉排序树，基本思想：

• 在二叉树的结点里存储字典的信息。
• 为二叉树安排好一种字典数据项的存储方式，使得字典查询等操作可以利用二叉树的平均高度远小于树中结点个数的性质，使检索能够沿着树中路径进行，从而获得较高的检索效率。

二叉排序树实现的关键是要保证关键码有序。

性质

二叉排序树的性质：

• 根结点保存着一个数据项(及其关键码)。
• 如果其左子树不为空，那其左子树的所有结点保存的关键值均小于根结点保存的关键码。
• 如果其右子树不为空，那么其右子树的所有结点保存的关键码均大于它的根结点保存的关键码。
• 非空的左子树和右子树也是二叉排序树。

显然，如果对一棵二叉排序树做中序遍历，那么得到的将是一个按照关键码值上升排序的序列。利用二分法检索得到的判定树就是二叉排序树。

同一集数据对应的二叉排序树并不唯一。例子：KEY = [36,65,18,7,60,89,43,57,96,52,74]

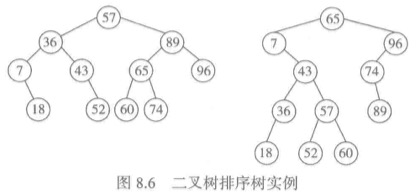
一棵结点中存储着关键码的二叉树是二叉排序树，当且仅当通过中序遍历这棵二叉树得到的关键码序列使一个递增序列。

二叉排序树既可以当做字典，把数据直接保存在树的结点里，有可以作为索引结构，实际数据另外存储，在二叉树的结点里与关键码关联的是数据的存储位置信息。

二叉排序上的检索

这里使用链接结构实现二叉排序树。

def bt_search(tree, key):
    bt = tree
    while bt is not None:
        entry = bt.data
        if key == entry:
            return entry.value
        elif key < entry:
            bt = bt.left
        else:
            bt = bt.right
    return None

二叉排序树的实现

插入操作和删除操作都需要修改树的结构。

1>插入操作

• 找到新结点的位置
• 把新结点正确连接到树中

这里有一个小问题，如果遇到与要插入数据的key一样的情况，怎么办？这里的处理方法，是用要插入的新值替换掉旧值，这样保证了字典中不会出现关键码重复的项。

插入数据的基本算法：

• 如果二叉树为空，就直接插入。
• 否则先搜索要插入的位置。
• 遇到应该走向左子树而左子树为空，或者应该走向右子树而右子树为空时，就找到了要插入的位置，构造新结点，然后插入。
• 遇到结点里的关键码与检索关键码一样时，直接替换。

2>删除操作

删除操作有两点要求：

• 删除数据项
• 保证其他数据项仍然可以正常查询和使用，也就是说，删除原来的数据项之后，剩下的结构还必须是一个二叉排序树。

基本思路：

• 找到要删除的结点，将其去除。
• 如果破坏了结构，就在被删除结点的周围做尽可能小的局部调整。

假设已经确定了应该删除结点q，它是p的左子结点，那么这时候有两种情况：

• 1. q是叶结点，这时只需要将其父结点p到q的引用设置为None，删除就完成。也就是p.left = None。
• 2. q不是叶结点，那么久不能简单删除了，需要把q的子树连接到删除q之后的树中，而且要保证关键码的顺序。这个时候又分为两种情况：
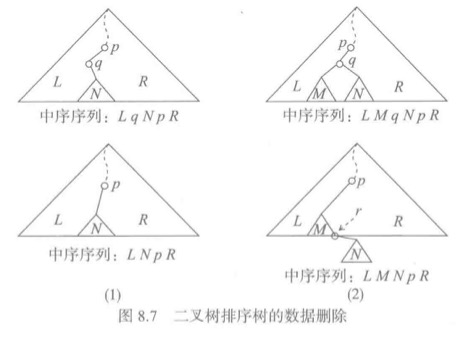
• * 如果q没有左子结点，这个时候只需要把q的右子树改为p的左子树，也就是p.left = q.right。下图1
• * 如果q有左子树，这时先找到q的左子树的最右结点r(也就是q的左子树中最大的结点)，这个时候r.right必然是None。然后用q的左子结点代替q作为p的左子结点，也就是p.left = q.left。并把q的右子树作为r的右子树。r.right=q.right。下图2

当q为p的右子结点的情况类似。

 

class DictBinTree:
    def __init__(self):
        self.root = None
    
    def is_empty(self):
        return self.root is None
    
    def search(self, key):
        bt = self.root
        while bt is not None:
            entry = bt.data
            if key == entry:
                return entry.value
            elif key < entry:
                bt = bt.left
            else:
                bt = bt.right
        return None
    
    def insert(self, key, value):
        '''
        插入操作，分析见上面
        '''
        bt = self.root
        if bt is None:
            self.root = BinTNode(Assoc(key, value))
        while True:
            entry = bt.data
            if key < entry.key:
                if bt.left is None：
                    bt.left = BinTNode(Assoc(key, value))
                    return 
                bt = bt.left
            elif key > entry.key:
                if  bt.right is None:
                    bt.right = BinTNode(Assoc(key, value))
                    return
                bt = bt.right
            else:
                bt.data.value = value
                return 
        
    def values(self):
        '''
        中序遍历，得到一个值的迭代器
        '''
        t, s = self.root, SStack()
        while t is not None or not s.is_empty():
            while t is not None:
                s.push(t)
                t = t.left
            t = s.pop()
            yield t.data.value
            t = t.right
    
    def entries(self):
        '''
        中序遍历，得到一个(key,value)的迭代器
        '''
        t, s = self.root, SStack()
        while t is not None or not s.is_empty():
            while t is not None:
                s.push(t)
                t = t.left
            t = s.pop()
            yield t.data.key, t.data.value   #这里如果yield t.data是不安全的，这是一个对象，而通过这个对象可以更改key的值。这样就破坏了字典的结构。
            t = t.right
    
    def delete(self, key):
        p, q = None, self.root   # p为q的父结点
        while q is not None and q.data.key != key:
            p = q
            if key < q.data.key:
                q = q.left
            else:
                q = q.right
        if q is None:  # 没有找到关键码key
            return 
        if q.left is None:  # q没有左子结点，只需把q的右子树修改为p的左子树。也包括也结点的情况，因为是叶结点的时候，q.right==None。
            if p is None:  # q是根结点
                self.root = q.right  # 将q的右子结点设置为根结点
            elif q is p.left:  # q是p的左子结点:
                p.left = q.right
            else:  # q是p的右子结点
                p.right = q.right
        # q有左子结点
        r = q.left  # 找到q左子树的最右结点
        while r.right is not right:
            r = r.right
        r.right = q.right  
        if p is None: # q是根结点
            self.root = q.left
        elif p.left is q:
            p.left = q.left
        else:
            p.right = q.left        

性质分析

删除操作，插入操作，检索操作都依赖于树的结构，也就是二叉树的高度。如果树的结构良好，那么这些开销就是O(logn)。如果树结构畸形，那么最差是O(n)。实际上下面的如果不断往这个结构里面插入关键码递增的序列，那么得到的就是一棵高度等于结点个数的最差的二叉排序树。因此，这中情况也不少见。

还有一个问题，每次如果q的左子结点不是空删除操作，都会增加二叉树这条路径上的长度。这样，随着字典操作的反复插入删除，用二叉排序树构建的字典效率就不断降低。

二叉树排序树中插入，删除，检索操作的空间复杂度都是O(1)。

2、最佳二叉排序树

一般的二叉排序树有可能出现检索路径特别长的情况，因此，用一个标准来判断什么样的排序二叉树才是最好的，这个标准应该是基于检索效率的。

平均检索长度

用key检索的时候，key可能存在，也可能不存在。

当树中存在key的检索情况时，能找到存储着相应数据项的结点，这种检索称之为成功检索。否则为失败检索。如果用一个外部结点把失败检索都连接到排序二叉树中组成一个新的二叉树，就会发现这个新的二叉树是原二叉树的扩充二叉树。例如下图：

然后按照中序遍历这种扩充二叉树，就会发现得到的序列使一个内部结点与外部结点交叉的序列。也就是说一个叶结点，一个内部结点。我们称这样的序列为扩充二叉排序树的对称序列。

虽然一个排序的关键码序列，存在不同的二叉排序树，但是，它们的扩充二叉排序树的对称序列是完全一样的。

在这种扩充二叉排序树里，它的关键码平均检索长度是这样的：

 

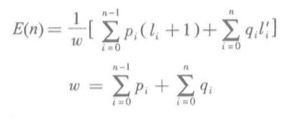
• li是内部结点i的层数，l'i是外部结点的层数。
• pi是检索内部结点i的关键码的频度(就是成功检索i频度)，确定一个内部结点，需要做的比较次数是结点所在的层数加1。
• qi是被检索关码属于外部结点i代表的关键码结合的频度(就是在一个范围内失败检索的频度)，检索到一个外部结点的比较次数签好等于该结点所在的层数。
• 这样，pi/w就是检索内部结点i的关键码概率。qi/w就是被检索的关键码属于外部结点i的关键码集合的概率。

最佳二叉排序树就是使检索的平均次数达到最少的二叉排序树，也就是说，它应该使E(n)的值达到最小。

简单情况：检索概率相同

 

 

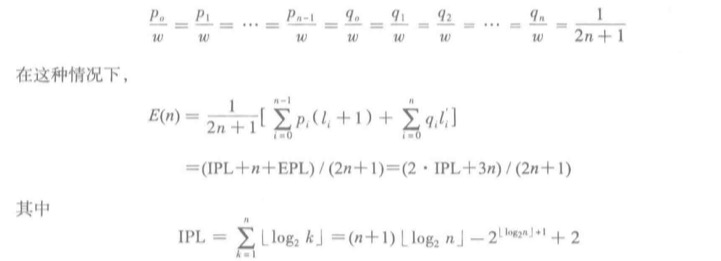
这时IPL最小的时候这棵树最佳，也就是说最低的树是最好的。

现在考虑最佳二叉排序树的构造方法。

基本思想如下：

• low=0, heigh = len(a) - 1
• m = (low+high) /2
• 把a[m]存入正在构造的二叉排序树的根结点t，然后递归的：
• 将基于元素片段a[low:m-1]构造的二叉排序树作为t的左子树。
• 将基于元素片段a[m+1:high]构造的二叉排序树作为t的右子树。
• 片段为空时直接返回None，表示空树。

O(n)的复杂度。

class DictOptBinTree(DictBinTree):
    def __init__(self, seq):
        DictBinTree.__init__(self):
        data = sorted(seq)
        self.root = DictOptBinTree.buildOBT(data, 0, len(data)-1)
    
    @staticmethod
    def buildOBT(data, start, end):
        if start > end:
            return None:
        mid = (end + start) // 2
        left = DictOptBinTree.bulidOBT(data, start, mid-1)
        right = DictOptBinTree.bulidOBT(data, mid+1, end)
        return BinTNode(Assoc(*data[mid]), left, right)

注意，反复插入和删除只能保证二叉排序树的结构完整，并不能保证二叉树的最佳性质。反复插入和删除之后，通常导致字典的性能变差。

3、一般情况下的最佳二叉排序树。

暂时没有弄懂，先略。

七、平衡二叉树

虽然最佳二叉排序树很好，可以保证最佳的检索效率，但是它只适用于静态字典，并不适合动态字典，因为，不能很好的支持插入和删除操作。

那么这时候，如果需要设计一个即能支持高效检索，又能支持动态操作的排序树结构。

也就是平衡二叉树，又称AVL树，与之类似的结构还有红黑树和B树等。

1、定义和性质

平衡二叉树的基本考虑是：树中的每个结点的左右子树的高度都平衡，这样就不会出现特别长的路径。

定义：平衡二叉排序树是一类特殊的二叉排序树，它或者为空树，或者其左右子树都是平衡二叉排序树，而且其左右子树的高度之差的绝对值不超过1。

这里用一个平衡因子BF来描述结点平衡，BF的值是左子树的高度减去右子树的高度，因此在平衡二叉树中，它的值只有-1，0，1三种情况。

显然，完全二叉树和等概率情况的最佳二叉排序树都是平衡二叉树。

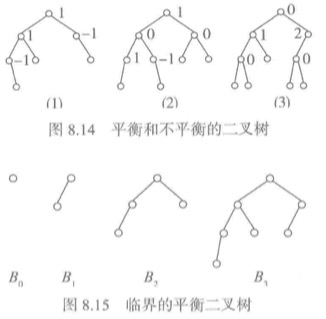
上图1中(1)和(2)是平衡二叉树。(3)有一个结点的BF值是2，因此不是平衡二叉树。

2、AVL树的实现

AVL树也是二叉排序树，不同的是AVL树在插入和删除的时候，不仅要保持树的结构和树中结点关键码的正确排序，还必须维持树的平衡。

基本定义

为了实现AVL树，二叉树的每个结点里都必须增加一个平衡因子记录。

class AVLNode(BinTNode):
    def __init__(self, data):
        BinTNode.__init__(self, data)
        self.bt = 0

3、插入操作

插入后的失衡的调整

首先应该考虑，如果在检索的插入位置的过程中，所有途径的结点的BF值都是0，那么实际插入结点后不会导致这些结点失衡。只是把它们的BF修改为-1或1。其余结点的BF的值不变，整棵树也不会失衡。

如果不是上面的情况，那么就一定存在一棵包含实际插入点的最小非平衡子树，也就是说那棵包含新结点插入位置的、其根结点的BF非0的最小子树。如果插入新结点后这棵子树扔保存平衡，那么整个二叉树保存平衡。

假设插入结点所在的最小非平衡子树的根结点是a，如果左子树较高，也就是a结点的BF=1时(下图1)，如果插入点在a的右子树，插入后之后，只需调整相关结点的BF值即可。如果插入点在a的左子树，那么就会破坏a的平衡，必须设法恢复a的平衡，恢复方法是从较高的子树调整结点到另外一个子树，降低其高度(下图2)。

 

 

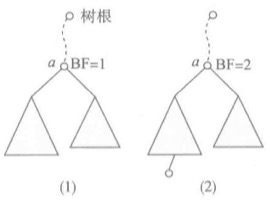
具体的恢复操作，有四种情况处理：

• LL型(a的左子树较高，新结点插入在a的左子树的左子树)。
• LR型(a的左子树较高，新结点插入在a的左子树的右子树)。
• RR型(a的右子树较高，新结点插入在a的右子树的右子树)。
• RL型(a的右子树较高，新结点插入在a的右子树的左子树)。

其中后两种情况与前两种情况一一对应。

LL(RR)失衡和调整

插入操作前，考虑a的左子树(b是根结点)较高的情况，因为a是最小的非平衡子树的根，因此b一定是平衡的。也就是的的BF=0(下图1)。

LL就是新结点插入b的左子树(A)中(下图2)，导致出现失衡的情况。

这种情况下，做一个顺时针旋转，调整结点b和a的位置关系，将结点b作为调整后子树的根结点，a作为b的右子结点，b原来的右子树B作为a的左子树。这时a的两棵子树同高，b的两棵子树也同高，调整完成(下图3)。

# 将LL调整成AVL树的一个静态方法

@staticmenthod
def LL(a, b):
    a.left = b.right
    b.right = a
    a.bf = b.bf = 0
    return b

那么与之对应的RR调整也是类似。

@staticmenthod
def RR(a, b):
    a.right = b.left
    b.left = a
    a.bf = b.bf = 0
    return b

LR(RL)失衡和调整

先考虑a的左子树(b是根结点)较高的情况，因为a是最小的非平衡子树的根，因此b一定是平衡的。也就是的的BF=0(下图1)。这时二叉树的对称序列是AbBcCaD。

这时要插入的结点在b的右子树下，然后二叉树失衡(下图2)。

进行调整使其重新平衡(下图3)。这时二叉树的对称序列是AbBcCaD，表明调整正确。调整方法加下面代码。

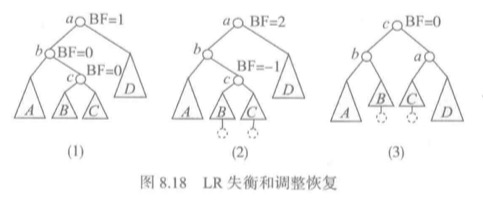
@staticmethod
def LR(a, b):
    c = b.right  # 设b的右子树为c
    a.left = c.right  # 将a的左子树设置为c的右子树(C)
    b.right = c.left  # 将b的右子树设置为c的左子树(B)
    c.left = b
    c.right = a
    
    if c.bf == 0:  # 本身就是插入点
        a.bf = b.bf =0
        
    elif c.bf == 1: # 新结点插入到c的左子树上
        a.bf = -1
        b.bf = 0
    
    else:
        a.bf = 0
        b.bf = 1
    c.bf = 0
    return c

RL失衡情况与此类似

@staticmethod
def RL(a, b):
    c = b.left
    a.right, b.left = c.left, c.right
    c.left, c.right = a, b
    if c.bf == 0:    # c 本身就是插入结点
        a.bf = 0
        b.bf = 0
    elif c.bf == 1:  # 新结点在 c 的左子树
        a.bf = 0
        b.bf = -1
    else:            # 新结点在 c 的右子树
        a.bf = 1
        b.bf = 0
    c.bf = 0 
    return c

def insert(self, key, value):
    '''
    复杂度O(logn)
    '''
    a = p = self._root
    if a is None:
        self._root = AVLNode(Assoc(key, value))
        return
    pa = q = None  # 维持 pa, q 为 a, p 的父结点
    while p:       # 确定插入位置及最小非平衡子树
        if key == p.data.key:  # key存在，修改关联值
            p.data.value = value
            return
        if p.bf != 0:
            pa, a = q, p  # 已知最小非平衡子树
        q = p
        if key < p.data.key:
            p = p.left
        else:
            p = p.right
    # q 是插入点的父结点，parent，a 记录最小非平衡子树
    node = AVLNode(Assoc(key, value))
    if key < q.data.key:
        q.left = node   # 作为左子结点
    else:
        q.right = node  # 或右子结点
    # 新结点已插入，a 是最小不平衡子树
    if key < a.data.key:  # 新结点在 a 的左子树
        p = b = a.left
        d = 1
    else:                # 新结点在 a 的右子树
        p = b = a.right
        d = -1   # d记录新结点在a哪棵子树
    # 修改 b 到新结点路上各结点的BF值，b 为 a 的子结点
    while p != node:     # node 一定存在，不用判断 p 空
        if key < p.data.key:   # p 的左子树增高
            p.bf = 1
            p = p.left
        else:                  # p的右子树增高
            p.bf = -1
            p = p.right
    if a.bf == 0:   # a原BF为0，不会失衡
        a.bf = d
        return
    if a.bf == -d:  # 新结点在较低子树里
        a.bf = 0
        return
    # 新结点在较高子树，失衡，必须调整
    if d == 1:       # 新结点在 a 的左子树
        if b.bf == 1:
            b = DictAVL.LL(a, b)  # LL 调整
        else:
            b = DictAVL.LR(a, b)  # LR 调整
    else:            # 新结点在 a 的右子树
        if b.bf == -1:
            b = DictAVL.RR(a, b)  # RR 调整
        else:
            b = DictAVL.RL(a, b)  # RL 调整

    if pa is None:
        self._root = b    # 原 a 为树根
    else:
        if pa.left == a:
            pa.left = b
        else:
            pa.right = b

删除操作与插入操作类似

• 检索需要删除的结点
• 把删除任意结点的问题变成删除某棵子树的最右结点的问题，为此只需要找到被删结点左子树的最右结点并交换两个结点的位置。
• 实际删除结点
• 如果出现失衡就调整树结构，恢复平衡。

几种二叉排序树结构的比较:

• 简单的二叉排序树能支持字典操作，其检索操作的平均效率高，插入和删除操作的实现比较简单，平均操作效率也是O(logn)。但是有指明缺点，就是操作的高效率并没有保证。这种树的结构是在插入和删除的动态操作中自然形成的，没有任何控制，因此有可能出现结构退化的情况。
• 最佳二叉排序树构造比较耗时，但是能保证最高的检索效率。不过问题是简单二叉排序树是一样的，在反复插入和删除操作之后，会降低它的性能。因此，它不适合动态字典。
• AVL树的检索效率与最佳二叉树一样。而且，它在不断插入和删除之后，不会出现结构失衡的情况。适合实现动态字典。这种结构的缺点就是操作实现比较复杂。