二叉树和树
目录
- 一、树形结构特征
- 二、二叉树:概念和性质
- 三、二叉树的list实现
- 四、优先队列
- 五、离散事件模拟
- 六、二叉树的类实现(链接实现)
- 七、哈夫曼树
- 八、树和树林
一、树形结构特征
树形结构是由结点和结点之间的连接关系构成,它与表线性结构不同,特征包括:
- 一个结构如果不为空,其中就存在着唯一的起始结点,称为树根。
- 按照结构外的连接关系,树根外的其余结点都有且只有一个前驱,可以有0个或者多个后继。
- 结构里所有结点都在树根结点通过后继关系可达的节点集合里。
- 结点之间的联系不会形成循环关系。
- 从这种结构的任意两个不同的节点出发,通过后继关系可达的两个结点集合,或者互不相交,或者一个集合是另外一个集合的子集。
二、二叉树:概念和性质
二叉树是树中的每个结点最多关联两个后继结点。
- 一个结点的关联数是0或1或2
- 一个结点的后继结点明确分左右,或为左结点,或为右结点。
1、概念和性质
定义和图示
二叉树的子树可以为空,并且子树有明确的左右之分,如果根结点的两颗子树都为空,那么这就是一棵只包含根结点的二叉树。

几个基本概念
- 不包含任何结点的二叉树称为空树
- 只包含一个结点的二叉树是一棵单点树
- 一棵二叉树的根结点称为该树的子树根结点的父结点。子树的根结点称为二叉树树根结点的子结点。
- 一个二叉树里有些结点的两个子树都是空,没有子结点,这种结点称之为树叶。树中其余结点称为分支结点。
- 一个结点的子结点个数称为该结点的度数。二叉树中树叶结点的度数为0,分支结点的度数为1或者2。
路径、结点的层和树的高度
- 从一个祖先结点到任何子孙结点都有一系列边,这样的一系列边首尾相连就成为了一条路径,我们把边的个数称为该路径的长度。
- 从树根到树中任一结点的路径长度就是该结点所在的层数。
- 一棵二叉树的高度是树中结点的最大层数(也就是这棵树里的最长路径的长度)。
二叉树的性质
二叉树最重要的性质就是树的高度和树中可以容纳的最大结点个数之间的关系。
如果将树跟线性表做比较,那么树的高度就类似于表的长度。但是在长为n的表中只能容纳n个结点。而在高为n的二叉树中可以容纳2n+1个结点。
- 性质1:在非空二叉树第i层中最多有2i个结点(i>=0)
- 性质2:高度为h的二叉树最多有(2h+1-1)个结点(h>=0)
- 性质3:对于任何非空二叉树,如果叶结点的个数为n0,度数为2的结点个数为n2。那么n0=n2+1
满二叉树,扩充二叉树

如果一个二叉树中所有的分支结点的度数都是2,那么它就是一棵满二叉树。
满二叉树的叶节点比分支结点多1。跟二叉树的性质3一样。
对于二叉树T,加入足够多的新叶结点,使T的原有结点都变成度数为2的分支结点,得到的二叉树称为T的扩充二叉树。扩充二叉树中新增的结点称为其外部结点,原树T的结点称为其内部结点。
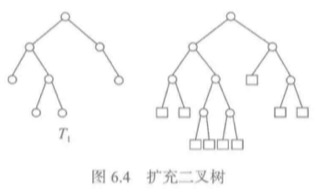
扩充二叉树的外部路径长度E是从树根到树中各外部结点的路径长度之和,内部路径长度I是从树根到树中各内部结点的路径长度之和。如果该树拥有n个内部结点,那么E=I+2*n。
完全二叉树
对于一棵高度为h的二叉树,如果其第0层到第h-1层的结点都满,并且如果下一层的结点都不满,则所有结点在最左边连续排列,空位都在右边,那么这样的二叉树就是完全二叉树。
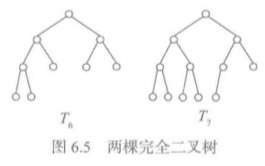
* 性质1:n个结点的完全二叉树高度h不大于log2n的最大整数。
* 性质2:完全二叉树如果n个结点的完全二叉树的结点按照层次从左到右的顺序从0开始编号,对于任一结点都有:
1. 序号为0的结点是根。
2. 对于i>0,其父节点的编号是(i-1)/2。
3. 2*i+1<n,其左子节点的序号为2*i+1,否则它没有左子结点。
4. 2*i+2<n,其右子结点的序号为2*i+2,否则它没有右子结点。
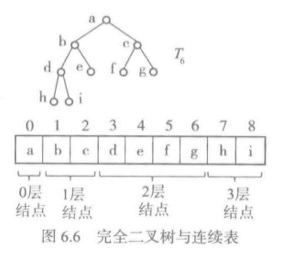
这说明从完全二叉树到线性结构有很自然的双向映射,可以很方便地从相应线性结构恢复完全二叉树。
2、抽象数据类型

结点是二叉树的基础,通常主要用结点保存与应用有关的信息。此外,还需要记录二叉树的结构信息,保证可以检查结点的父子关系。
二叉树的基本操作应该包括创建二叉树。构造一棵二叉树需要基于两棵已有的二叉树和希望保存在树根结点的一项数据。
3、遍历二叉树
每个二叉树都有唯一的根结点,可以将其看做是这个二叉树的唯一标识,它是基于树结构处理过程的入口。遍历二叉树,就是按照某种系统化的方式访问二叉树里的每个结点一次。
遍历二叉树就像前面讨论过的状态搜索,以根为起始点,存在两种基本方式:
- 深度优先遍历,顺着一条路径尽可能向前探索,必要的时候回溯。对于二叉树,最基本的回溯情况是检查完一个叶节点。由于无路可走,只能回头。
- 宽度优先遍历,在所有的路径上齐头并进。
深度优先遍历
按照深度优先方式变量一棵二叉树,需要做三件事情:遍历左子树(L),遍历右子树(R),和访问根节点(D)。
根据这三种工作的不同顺序可以分为三种遍历顺序(假设总是先处理左子树,不然就是6种):
- 先根序遍历(按照DLR顺序)
- 中根序遍历(按照LDR顺序)
- 后根序遍历(按照LRD顺序)
例子:下图

- 先根序遍历是ABDHEICFJKG
- 中根序遍历是DHBEIAJFKCG
- 后根序变量是HDIEBJKFGCA
按照先根序遍历得到的结点序列称为先根序列。
按照中根序遍历得到的结点序列称为中根序列。
按照后根序遍历得到的结点序列称为后根序列。
如果二叉树中每个结点都有唯一标识,就可以同结点标识描述这些序列。显然,给定一个二叉树唯一确定了它的先根序列、后根序列和中根序列,但是给定一棵二叉树的任一一种遍历序列,都无法唯一确定相应的二叉树。
如果知道了一棵二叉树的对称序列,又知道另一遍历序列,就可以唯一确定这个二叉树。
宽度优先遍历
宽度优先是按照路径长度由近到远访问,这种遍历不能写成一个递归过程。宽度优先遍历又称为按层次顺序遍历,这样遍历产生的结点序列称为二叉树的层次序列。
上面例子中按照宽度优先遍历的层次序列是:ABCDEFGHIJK
遍历与搜索
一次二叉树遍历也就是一次覆盖整个状态的空间搜索,因此,前面关于空间状态搜索的方法和实现技术都可以原样移植到二叉树遍历问题中。
二叉树的特点是一个结点最多有两个子结点,因此从一条路径走下去不会与另外一条路径相交,就不会出现循环问题。因此算法比空间状态搜索要简化一些。
三、二叉树的list实现
二叉树的结点就是一个三元组,元素是左右子树和本结点数据。因此list和tuple都可以实现,如果要实现一种非变动的二叉树,用tuple,要实现可以修改结构的二叉树,用list。
1、设计和实现
利用list实现二叉树很容易。采用下面的设计
- 空树用None表示
- 非空子树用包含三个元素的表[d,l,r]表示。其中d表示根结点元素,l表示左子树,r表示右子树。
例如:下图
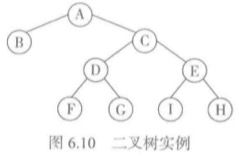
如果使用list来表示,就是['A',
['B', None, None],
['C',
['D', ['F', None, None], ['G', None, None]],
['E', ['I', None, None], ['H', None, None]],
]

class BTree: def __init__(self, data, left=None, right=None): if not isinstance(right, BTree) or if not isinstance(left, BTree): raise TypeError self.tree = [data, left, right] def is_empty_bintree(self): return self.tree is None def root(self): return self.tree[0] def left(self): return self.tree[1] def right(self): return self.tree[2] def set_root(self, data): self.tree[0] = data def set_left(self, left): if not isinstance(left, BTree): raise TypeError self.tree[1] = left def set_right(self, right): if not isinstance(right, BTree): raise TypeError self.tree[2] = right
2、二叉树的简单应用:表达式树
二元表达式和二叉树
二元表达式可以很自然映射到二叉树中,因为它的运算符都是二元的。
- 以基本运算对象(数和变量)作为叶结点中的数据
- 以云素符作为分子结点的数据,其中两个子树是它的运算对象。子树可以是基本运算对象,也可以是任意复杂的二元表达式。
例子:下图

- 先根序遍历得到x-ab+/cde,正是该表达式的前缀形式。
- 中跟序遍历得到a-bxc/d+e,正是该表达式的中缀形式(缺少括号)。
- 后根序遍历得到ab-cd/e+x,正是该表达式的后缀形式。
构造表达式
因为建立的表达式不会变化,因此使用tuple的三元组实现比较合理。
例如:3 * (2+5)映射到这种结构中就是('*',3,('+',2, 5))
这种结构由两部分组成:
- 如果是序对,就是运算符作用于运算对象的符合表达式。
- 否则就是基本表达式,也就是数或者变量。
def make_sum(a, b):
return ('+', a, b)
def make_prod(a, b):
return ('*', a, b)
def make_diff(a, b):
return ('-', a, b)
def make_div(a, b):
return ('/', a, b)
e1 = makeprod(3, make_num(2, 5))
在定义表达式处理函数的时候,经常需要区分基本表达式还是符合表达式。
def is_basic_exp(a): return not isinstance(a, tuple)
表达式求值
表达式规则:
- 对表达式里的数和变量,其值就是它们自身。
- 其他表达式根据运算符的情况处理,可以定义专门处理函数。
- 如一个运算符的两个运算对象都是数,就可以求出这个数值。

def eval_exp(e): if is_basic_exp(e): return e op, a, b = e[0], eval_exp(e[1]), eval_exp(e[2]) if op == '+': return eval_num(a, b) elif op == '-': return eval_diff(a, b) elif op == '*': return eval_prod(a, b) elif op == '/': return eval_div(a, b) else: raise ValueError('Unknown operator', op) def eval_sum(a, b): if is_number(a) and is_number(b): return a +b if is_number(a) and a == 0: return b if is_number(b) and b == 0: return a return make_sum(a, b)
四、优先队列
1、概念
优先队列的特点是存入其中的每项数据都另外附有一个数值,表示这个项的优先程度,称为优先队列。优先队列应该保证,在任何时候访问或者弹出的,总是当时这个结构里保存的所有元素中优先级最高的。
允许不同元素具有相同优先级的情况,不过如果优先级相同还要先进先出,那么效率要低一些,如果优先级相同,不比先进先出,那么存在效率高的实现。
2、基于线性表的实现
有关实现方法的考虑
由于连续表可以存储数据元素,显然有可能作为优先队列的实现基础。数据项在连续表里的存储顺序可以用来表示数据之间的某种顺序关系,对于优先队列,这个顺序可以用来表示优先级关系。例如,让数据的存储位置按照顺序排列。
有两种实现方案:
- 在存入数据时,始终保证表中元素按优先顺序排列(数据不变式),这样任何时候都可以直接取到当时在表里的最优先元素。(存入耗时,检索简单)
- 存入数据时,采用最简单的方式存入。需要取用时,通过检索找到最优先的元素。 (存入简单,检索耗时)
基于list实现的优先队列
用第一种方案实现。

class PrioQueueError(ValueError): pass class PrioQue: def __init__(self, elist=[]): self.elems = list(elist) #这里注意默认参数elist,它是一个可变对象,会共享,因此使用list转换,复制成另外一个对象。 self.elems.sort(reverse=True) def insert(self, e): ''' 找到正确位置,插入元素。可以使用二分法找到位置,不过插入的时候还是要O(n)的复杂度。也可以使用插入排序的方式,在找位置的同时,将小的元素后移。 ''' i = len(self.elems) - 1 while i >= 0: if self.elems[i] <= e: i -= 1 else: break self.elems.insert(i+1, e) def is_empty(self): return not self.elems def peek(self): if self.is_empty(): raise PrioQueueError('in top') return self.elems[-1] def dequeue(self): if self.is_empty(): raise PrioQueueError('in pop') return self.elems.pop()
3、树形结构和堆
线性和树形结构
分析上面线性表实现优先队列效率低的原因。如果是顺序表,需要移动O(n)个元素,如果是链表,需要爬行O(n)步。这就意味着如果不改变数据的线性顺序存储方式,就不可能突破O(n)的复杂限制。
因此要操作更高,就必须考虑其他数据结构的组织方式。
堆及其性质
采用树形结构实现有线队列的一种有效技术成为堆。从结构上来看,堆就是结点里存储数据的完全二叉树,但是堆中数据要满足一种特殊的堆序,那就是任一个结点里所存的数据先于或等于其子结点里的数据。
- 在一个堆中从树根到任何一个叶结点的路径上,各结点里所存的数据按规定的优先关系递减。
- 堆中最优先的元素必定位于二叉树的根结点里。O(1)时间就能得到
- 位于树中不同路径上的元素,不关心其顺序关系。
如果所要求的序是小元素优先,那么构造出来的堆就是小顶堆。堆中每个结点的数据均小于或者等于其子结点的数据。如果要求大元素优先,那么就是大堆顶。
一个堆是按照堆序排序好的完全二叉树。
- 在一个堆的最后加上一个元素,它是完全二叉树,但不一定是堆(因为未必满足堆序)。
- 一个堆去掉堆顶,自然形成的两个子堆仍然满足堆序。但是如果在这两个子堆上随意加一根元素,那么形成的是一个完全二叉树,并不一定是堆(跟上面一样,不一定满足堆序)。
- 去掉堆中的最后一个元素,剩下的仍然是一个堆。
4、优先队列的堆实现
解决堆插入和删除的关键操作称为筛选,又分为向上筛选,和向下筛选。
插入元素和向上筛选
向堆的最后插入一个元素,如果要把它恢复成堆,必须做一个向上筛选的操作。
向上筛选的方法是:不断用新加入的元素与其父结点的数据比较,如果e较小(小顶堆)就交换位置,使e上移,直到e的父结点的数据不大于e或者e到达根结点的时候停止,这时就将它重新恢复为一个堆(因为满足堆序)了。
- 把新加入的元素放在已有元素之后,执行向上筛选操作。
- 向上筛选操作中比较次数不会超过二叉树中最长路径的长度。因此,加入操作可以在O(logn)时间完成。
弹出元素和向下筛选
弹出元素的操作分三步:
- 弹出堆顶
- 将最后一个元素放到堆顶
- 向下筛选
向下筛选的过程:
- 用e与A、B两个子堆的顶元素比较。最小者为堆顶。
- 如果e不是最小,最小的必为A或B的根。
- 假设这里是A的根最小,那么将它移到堆顶,相当于删除了A的顶元素。
- 下面考虑把e放入去掉堆顶的A,然后继续让下比较。
- 如果是B的根最小的话,也是同样处理
- 在某次比较中e是最小,那么它为顶的局部树就是一个堆,整个结构也成堆。
- 或者e已经到底,也就是它没有子结点。那么整个结构也称为堆。
由此可以看出弹出操作是O(logn)复杂度,主要是取决于向下筛选的操作。
基于堆的优先队列类

class PrioQueue: def __init__(self, elist=[]): self.elems = list(elist) if elist: self.buildheap() def is_empty(self): return not self.elems def peek(self): if self.is_empty(): raise PrioQueueError('in peek') return self.elems[0] def enqueue(self, e): ''' 插入的时候,并没有直接存入,而是拿着它是跟父结点比较。 ''' self.elems.append(None) self.siftup(e, len(self.elems)-1) def siftup(self, e, last): ''' 根据性质完全二叉树的子结点下标是i,父结点下标是(i-1)//2 ''' i, j = last, (last-1)//2 elems = self.elems while i > 0 and e < elems[j]: elems[i] = elems[j] i, j = j, (j-1)//2 elems[i] = e def dequeue(self): ''' 删除的时候,也没有直接把最后一个元素放到堆顶,而是拿着它去做比较 ''' if self.is_empty(): raise PrioQueueError('in dequeue') elems = self.elems e0 = elems[0] e = elems.pop() if len(elems)>0: self.siftdown(e, 0, len(elems)) return e0 def siftdown(self, e, begin, end): elems, i, j = self.elems, begin, begin*2+1 while j < end: if j+1 < end and elems[j+1] < elems[j]: #右子堆的堆顶元素小于左子堆的堆顶元素 j += 1 if e < elems[j]: # e是三个里面最小的。堆形成。 break elems[i] = elems[j] # 将最小的元素往上移为父结点 i, j = j, j*2+1 elems[i] = e def buildheap(self): end = len(self.elems) for i in range(end//2, -1, -1): # end//2以下的都是叶结点,因此它们也就是一个个堆,因此从这里开始向前,一个个向下筛选,形成堆。 self.siftdown(self.elems[i], i, end)
构建操作的复杂性
堆构建的操作时间复杂度是O(n)。但是这个操作只需要做一次。插入和删除的操作复杂度是O(logn),效率比较高。插入操作如果出现替换元素存储区的情况,可能有最坏的情况O(n)出现。它们所有的空间复杂度都是O(1)。
5、堆的应用:堆排序
如果在一个连续表里存储的数据是一个小顶堆,按照优先队列的操作方式反复弹出堆顶的元素,那么就能得到一个递增的序列。不过还有两个问题:
- 连续表里的初始元素通常不满足堆序,因此需要先进行初始建堆工作。
- 选出的元素存放在哪里,可不可以不使用其他空间。
第一个问题已经解决。第二个问题也好解决。随着堆弹出,堆中元素也越来越少,每弹出一个元素,表的后部就会空出一个位置,正好利用这空出的位置存放弹出的元素。

def heap_sort(elems): def shiftdown(elems, e, start, end): i, j = start, 2*start+1 while j < end: if j+1 < end and elems[j+1] < elems[j]: j += 1 if e < elems[j]: break elems[i] = elems[j] i, j = j, 2*j+1 elems[i] = e end = len(elems) for i in range(end//2, -1, -1): shiftdown(elems, elems[i], i, end) for i in range((end-1), 0, -1): e = elems[i] # 取出最后的元素,以备向下筛选,放入合适的位置。 elems[i] = elems[0] # 取出最小元素放到最后 shiftdown(elems, e, 0, i)
五、离散事件模拟
离散时间系统特征:
- 系统运行时候,不断发生一些随机事件
- 一个事件在某个时刻发生,其发生有可能导致其他时间在未来发生
例子:过境海关检查
- 车辆按照一定时间间隔到达,间隔有随机性,范围是[a,b]分钟
- 由于车辆的不同情况,每辆车的检查时间为[c,d]分钟。
- 海关可以开k个通道
- 希望理解开通不同数量的通道数对车辆通行的影响
1、通用的模拟框架
基本思路:按照事件发生的时间顺序处理,在模拟系统里用一个优先队列保存已知在将在某些特定时刻发生的事件,系统运行就是不断从优先队列里取出等待事件,一个个处理,直到模拟结束。
在一些时间的处理中,可能会引发新的事件,那么这些事件应该放入优先队列中,在它们发生的时候被系统处理。

# 通用的模拟器类 from random import randint from prioqueue import PrioQueue from queue_list import SQueue class Simulation: def __init__(self, duration): self.eventq = PrioQueue() self.time = 0 # 记录当前时间 self.duration = duration # 记录模拟的总时长 def run(self): while not self.eventq.is_empty(): event = self.eventq.dequeue() self.time = event.time() if self.time > self.duration: break event.run() def add_event(self, event): self.eventq.enqueue(event) def cur_time(self): return self.time class Event: def __init__(self, event_time, host): self.ctime = event_time self.host = host # 表示有关事件发生的模拟系统。 def __lt__(self, other_event): return self.ctime < other_event.ctime def __le__(self, other_event): return self.ctime <= other_event.ctime def host(self): return self.host def time(self): return self.ctime def run(self): pass
2、海关检查站模拟系统
系统的基本要求:
- 检查过程车辆,只模拟一个通行方向的检查。
- 车辆到达有随机性,按照每[a,b]分钟有一辆车到达
- 海关有k条检查通道,检查一辆车需要[c,d]分钟
- 到达的车辆在一条专用线路上排队等待,一旦有一个检查通道空闲,排队的第一个车辆进入该通道,如果车辆到达时,有空闲通道,那么立即进入空闲通道。
- 希望得到的数据是车辆的平均等待时间和通过检查站的平均时间。

class Customs: def __init__(self, gate_num, duration, arrive_interval, check_interval): self.simulation = Simulations(duration) #模拟s系统对象 self.waitline = SQueue() #等待队列 self.duration = duration #持续时间 self.gates = [0] * gate_num #检查通道 self.total_wait_time = 0 #总共等待时长 self.total_used_time = 0 self.car_num = 0 self.arrive_interval = arrive_interval # 在一个区间范围时间到达车辆 self.check_interval = check_interval # 在一个区间范围时间检查完毕车辆 def wait_time_acc(self, n): self.total_wait_time += n def total_time_acc(self, n): sel.total_used_time += n def car_count_1(self): self.car_num += 1 def add_event(self, event): self.simulation.add_event(event) def cur_time(self): return self.simulation.cur_time() def enqueue(self, car): self.waitline.enqueue(car) def has_queued_car(self): return not self.waitline.is_empty() def next_car(self): return self.waitline.dequeue() def find_gate(self): ''' 0表示空闲,1表示忙 ''' for i in range(len(self.gates)): if self.gates[i] == 0: return i return None def free_gate(self, i): if self.gates[i] == 1: self.gates[i] = 0 else: raise ValueError('Clear gate Error') def simulate(self): Arrive(0, self) self.simulation.run() self.statistics() def statistics(self): print("Simulate " + str(self.duration) + " minutes, for " + str(len(self.gates)) + " gates") print(self.car_num, "cars pass the customs") print("Average waiting time:", self.total_wait_time/self.car_num) print("Average passing time:", self.total_used_time/self.car_num) i = 0 while not self.waitline.is_empty(): #模拟时间结束后还有多辆车在等待 self.waitline.dequeue() i += 1 print(i, "cars are in waiting line.") class Car: def __init__(self, arrive_time): self.time = arrive_time def arrive_time(self): return self.time

class Arrive(Event): def __init__(self, arrive_time, customs): Event.__init__(self, arrive_time, customs) customs.add_event(self) def run(self): time, customs = self.time(), self.host() # event_log(time, "car arrive") # genarate the next Arrive event Arrive(time + randint(*customs.arrive_interval), customs) # deal with current Arrive car car = Car(time) if customs.has_queued_car(): customs.enqueue(car) return i = customs.find_gate() if i is not None: # event_log(time, "car check") Leave(time + randint(*customs.check_interval), i, car, customs) else: customs.enqueue(car) class Leave(Event): def __init__(self, leave_time, gate_num, car, customs): Event.__init__(self, leave_time, customs) self.car = car self.gate_num = gate_num customs.add_event(self) def run(self): time, customs = self.time(), self.host() # event_log(time, "car leave") customs.free_gate(self.gate_num) customs.car_count_1() customs.total_time_acc(time - self.car.arrive_time()) if customs.has_queued_car(): car = customs.next_car() i = customs.find_gate() # event_log(time, "car check") customs.wait_time_acc(time - car.arrive_time()) Leave(time + randint(*customs.check_interval), i, car, customs)
六、二叉树的类实现(链接实现)
与连续表的链接实现类似,用一个数据单元表示一个二叉树的结点,通过子结点链接建立结点之间的关系。
1、二叉树结点类
class BinTNode: def __init__(self, dat, left=None, right=None) self.data = dat self.left = left self.right = right t = BinTNode(1, BinTNode(2), BinTNode(3)) #一个二叉树 def count_BinTNode(t): ''' 统计树中结点的个数 ''' if t is None: return 0 else: return 1 + count_BinTNode(t.left) + count_BinTNode(t.right) def sum_BinTNode(t): ''' 统计树中保存数值之和 ''' if t is None: return 0 else: return t.data + sum_BinTNode(t.left) + sum_BinTNode(t.right)
可以看到,递归定义的二叉树操作具有统一的模式:
- 描述对空树的处理,应该直接给出结果。
- 描述非空树情况的处理。如何处理根结点,通过递归调用分别处理左,右子树,然后基于上述三个部分处理的结果得到对整个树的处理结果。
2、遍历算法
递归定义的遍历函数

def preorder(t, proc): #proc是具体的结点数据操作 if t is None: return proc(t.data) preorder(t.left) preorder(t.right)

def levelorder(t, proc): qu = SQueue() qu.enqueue(t) while not qu.is_empty(): t = qu.dequeue() if t is None: continue qu.enqueue(t.left) qu.enqueue(t.right) proc(t.data)
非递归的先根序遍历函数
一种实现思路:
- 由于采取先根序,遇到结点就应该先访问,下一步应该沿着树的左枝下行。
- 这时,树的右分支未访问,因此需要入栈记录。
- 遇到空树时回溯,取出栈中保存的一个右分支,像一棵二叉树一样遍历它。

def preorder_nonrec1(t, proc): ''' 自己实现的 ''' st = SStack() st.push(None) #放一个标志,为了让循环运行。什么都可以 while not st.is_empty(): proc(t.data) if t.right: st.push(t.right) if t.left: t = t.left else: t = st.pop() def preorder_nonrec(t, proc): ''' 书中例子 ''' st = SStack() while t or not st.is_empty(): while t is not None: proc(t.data) s.push(t.right) t = t.left t = st.pop()

def midorder_nonrec1(t, proc): ''' 中根序 ''' st = SStack() while t or not st.is_empty(): while t: st.push((t.data, t.right)) t = t.left data, t = st.pop() proc(data) def midorder_nonrec1(t, proc): ''' 给出例子实现 ''' s = SStack() while t or not s.is_empty(): while t: s.push(t) t = t.left t = s.pop() proc(t.data) t = t.right
时间复杂性,O(n)。空间复杂性,找到栈的最大深度,所以空间复杂度是O(logn),最坏的空间复杂度是O(n),全部是右分支的情况。
通过生成器函数遍历

def preorder_elems(t): st = SStack() while t or not st.is_empty(): while t is not None: yield t.data st.push(t.right) t = t.left t = st.pop()
非递归算法的一个重要用途就是作为实现迭代器的基础。
非递归的后根序遍历算法
在这种遍历中,每个根结点都要经过三次,第一次遇到它转到左子树,第二次遇到它转到右子树,第三次遇到它处理结点数据。

def postorder_nonrec(t, proc): st = SStack() while t or not st.is_empty(): while t is not None: st.push(t) if t.left: t = t.left else: t = t.right t = st.pop() proc(t.data) if not st.is_empty() and st.top().left == t: t = st.top.right else: t = None
注意:
- 内层循环找当前子树的最下最左结点,将其入栈后终止。
- 如果被访问的结点是其父结点的左子结点,那么转到其右边的兄弟结点
- 如果被处理的是其父的右子结点,将t设置为None,处理父结点元素
非递归的遍历时间复杂度都是O(n)
3、二叉树类

class BinTree: def __init__(self): self.root = None def is_empty(self): return self.root is None def root(self): return self.root def leftchild(self): return self.root.left def rightchild(self): return self.root.right def set_root(self, rootnode): self.root = rootnode def set_left(self, leftchild): self.root.left = leftchild def set_right(self, rightchild): self.root.right = rightchild def preorder_elements(self): st = SStack() t = self.root st.push(None) while not st.is_empty(): yield t.data if t.right: st.push(t.right) if t.left: t = t.left else: t = st.pop()
但是在这种表示中,求父结点的操作比较难实现,它相当于单链表结构的求前一个结点操作,只能通过一次从根开始的遍历才能实现,最坏的时间代价是O(n)。
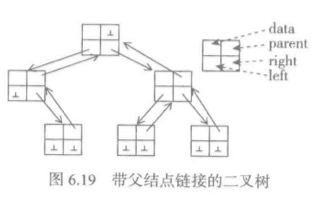
如果在工作中经常需要找父结点,可以考虑给每个结点增加一个父结点链接域,在设置子结点链接关系的同时设置好父结点链接。
七、哈夫曼树
哈夫曼树是一种很重要的二叉树。
1、哈夫曼树和哈夫曼算法
扩充二叉树的外部路径长度,是根到其外部结点的路径长度之和:E=l1+l2+l3+...+lm。
其中l是从根到外部结点的路径长度,m是外部结点的个数。
如果二叉树的外部路径带权,那么定义带权的扩充二叉树的外部路径长度为:WPL=w1*l1 + w2*l2 +w3*l3 + ... + wm*lm。其中wm是结点m的权。

上面图的两棵树带权的扩充二叉树,其中左边树的外部路径长度是2*2+2*3+2*6+2*6+2*9 = 2*(2+3+6+9) = 38。右边树的外部路径长度是9+6*2+(2+3)*3 = 36
由此可见,最规整的树未必路径最短。
哈夫曼树的定义
设有实数集W={w0,w1,...,wm-1},T是一棵扩充二叉树,其m个外部结点分别以wi(i=1,2,...n-1)为权,而且T的带权外部路径长度WPL在所有这样的扩充二叉树中达到最小,则称T为数据集W的最优二叉树或者哈夫曼树。
构造哈夫曼树的算法
- 算法的输入为实数集W={w0,w1,...,wm-1},。
- 在构造中维护一个包含k棵二叉树的集合F,开始时k=m,且F={T0,T1,...,Tm-1},其中每个Ti是一棵只包含权为wi的根结点的单点二叉树。
- 算法过程重复执行下面两个过程:1、构造一棵新的二叉树,其左右子树是从集合F中选取的两棵权最小的二叉树,其根结点的权值设置为这两棵子树的根结点的权值之和。2、将所选的两棵二叉树从E中删除,把新构造的二叉树加入F。
注意:给定集合W得到的哈夫曼树不唯一,如果T是集合W上的哈夫曼树,交换其中一个或者多个结点的左右子树,得到的仍然是W上的哈夫曼树。
例子:考虑实数集W={2,3,7,10,4,2,5}。从这个集合出发做一棵哈夫曼树。

- 找出最小的两个数2与2构成一棵二叉树,并将这两个结点从W中移除,将它们的根结点设置为两个数的权之和4。
- 将新构建的树加入集合W中,此时W={4,3,7,10,4,5}。
- 然后重复上面的过程,直到集合中剩下一个元素,就是最终的哈夫曼树。
2、哈夫曼算法的实现
构造算法需要维护一组二叉树,并且要知道每棵树的权值(跟结点的权值),那么可以考虑用二叉树的结点类来构造哈夫曼树,在树根结点记录树的权值。
此外,构造过程中,需要用一个优先队列存放这组二叉树,这样就能很容易选出权值最小的两棵二叉树。
这样算法的思路就很简单了:
- 从优先队列里选出两个权最小的元素(两棵二叉树)
- 基于所选取的二叉树构造一棵新的二叉树,其权值取两棵子树的权值之和,并将新构造的二叉树压入优先队列。
此外,还要注意两点:
- 优先队列定义一个序,这里采用权值小的在前(也就是小顶堆)。
- 需要检查优先队列的个数,这样当,队列剩一个元素的时候,就完成工作。

class HTNode(BinTNode): ''' 因为要做比较,所以定义一个小于的魔术方法,可以直接拿对象做比较 ''' def __lt__(self, othernoder): return self.data < othernoder.data class HuffmanPrioQ(PrioQueue): ''' 因为要检查剩余元素的个数,所以定义一个检查优先队列的长度函数。 ''' def number(self): return len(self.elems) def HuffmanTree(weights): ''' 可以用任何可迭代对象最为参数。 ''' trees = HuffmanPrioQ() for w in weights: trees.enqueue(HTNode(w)) while trees.number() > 1: t1 = trees.dequeue() t2 = trees.dequeue() t = HTNode(t1.data+t2.data, t1, t2) trees.enqueue(t) return trees.dequeue()
算法分析
第一个循环建立起m个二叉树复杂度是m(logm),因为加入一个元素需要做一次O(logm)复杂度的筛选,而前面建堆使用的方法只需要O(m),因此可以优化为前面那样的算法。
第二次循环需要做m-1次,因此需要O(logm)时间,上面整个算法的复杂度是O(mlogm)

def HuffmanTree(weights): ''' 可以用任何可迭代对象最为参数。 ''' htnodes = map(HTNode, weights) trees = HuffmanPrioQ(htnodes) while trees.number() > 1: t1 = trees.dequeue() t2 = trees.dequeue() t = HTNode(t1.data+t2.data, t1, t2) trees.enqueue(t) return trees.dequeue()
优化后的算法整个复杂度是O(m)。
算法执行的时候,需要构造一个包含2m-1个结点的树,因此其空间复杂度是O(m)。
3、哈夫曼编码
哈夫曼有很多应用,一个重要的应用就是哈夫曼编码。
定义
最优编码问题:
给定基本集合:C={c0,c1,...,cm-1},w={w0,w1,...,wm-1}其中集合C是需要编码的字符集合,W是C中个字符在实际信息传输中出现的频率。
要求:
- 用这种编码存储/传输时的平均开销最小
- 对任一对不同字符ci和cj,字符ci的编码不是cj编码的前缀。
哈夫曼编码的生成
哈夫曼提出了一种解决这个问题的方法,就是哈夫曼编码。构造方法就是构造出一棵哈夫曼树。
- 以w={w0,w1,...,wm-1}作为m个外部结点的权,以C={c0,c1,...,cm-1}作为外部结点标注。基于W构造出一棵哈夫曼树。
- 在的得到的哈夫曼树中,在从书中各个分子结点到其左子结点的边上标注二进制数字0,在所有到右子结点的边上标注数字1。
- 以根结点到一个叶结点的路径上的二进制数字序列,作为这个叶结点的标记字符的编码,这样就得到了一个哈夫曼编码。
哈夫曼编码在编码理论里有重要意义,是给定字符集的最优编码。
例子:
假设有字符和权值组{'a':2,'b':3,'c':7,'d':4,'e':10,'f':2,'h':5},要求通过哈夫曼的算法做出相应的哈夫曼编码。
首先按照权值做出一棵哈夫曼树(上图)。然后得到编码。a:0000,b:101,c:11,d:100,e:01,f:0001,h:001。现在假设收到报文:001010010000100000010101100,那么根据得到编码,解码正文为:hehadabed。

# 哈夫曼编码的算法 class HTNode2(HTNode): ''' 用key来存放标记值 ''' def __init__(self, dat, key=None, left=None, right= None): super().__init__(dat, left, right) self.key = key def htnodes(dic): ''' 将初始字典转化为结点迭代器。 ''' for key, value in dic.items(): yield HTNode(value, key) def get_huffman_tree(dic): ''' 获得哈夫曼树 ''' trees = HuffmanPrioQ(htnodes(dic)) while trees.number() > 1: t1 = trees.dequeue() t2 = trees.dequeue() t = HTNode(t1.data+t2.data, left=t1, right=t2) trees.enqueue(t) return trees.dequeue() def get_code(dic): ''' 获得编码字典 ''' t_node = get_huffman_tree(dic) tree = BinTree() tree.set_root(t_node) p = tree.root st = SStack() s = '' code_dic = {} st.push((s, None)) while not st.is_empty(): if p.right: st.push((s, p.right)) if p.left: p = p.left s += '0' if not p.right and not p.left: code_dic[s] = p.key s, p = st.pop() s += '1' return code_dic def htf_decode(str, dic): ''' 将字符串进行解码。这个匹配算法并不高效。 ''' htf_dic = get_code(dic) # 获得编码字典,key是编码,value是字符。 keys = list(htf_dic.keys()) results = '' i, j, m = 0, 0, 0 # i是str的下标。j是keys的下标,m是keys[j]的下标 while i < len(str) and j < len(keys): s = i # 暂存i,如果匹配不成功要进行回溯 while j < len(keys) and m < len(keys[j]): if str[s] == keys[j][m]: #字符相等,前进一位 s, m = s + 1, m + 1 else: # 匹配失败,j换个,回溯,m初始化归零。 s, j, m = i, j + 1, 0 if m == len(keys[j]): # 匹配成功一个字符,将其解码方法results中。 results += htf_dic[keys[j]] m, j, i = 0, 0, s if i == len(str): return results else: raise ValueError str = '000100111000100110111' dic = {'a': 2, 'b': 3, 'c': 7, 'd': 4, 'e': 10, 'f': 2, 'h': 5} s = htf_decode(str, dic) print(s)
上面代码构造出来的是一个不同于书上的哈夫曼树(哈夫曼树并不唯一,前面说过的),它的结构是这样的。

因此它的编码是这样的。{'00': 'c', '010': 'b', '011': 'd', '1000': 'f', '1001': 'a', '101': 'h', '11': 'e'}。
八、树和树林
现在考虑一般的树和树的集合,也就是树林。
1、实例和表示
树形结构具有明显的层次性,其中的高层元素可能与低层元素有关,同层元素之间相互无关,也没有从低层到高层的关联。
实际生活中有很多事物可以抽象成一种树形结构,比如:家族关系。公司的组织架构,复杂机械设备的零部件等。
例子:一个四代同堂的关系。曾祖有三个孩子,第二代有分别有两个,一个,三个。第三代已经有第四代,一共14人。
- 所有人的集合是:N={A,B,C,D,E,F,G,H,I,J,K,L,M,N}.
- 反应家庭结构的父子关系可以表示为:R={(A,B),(A,C),(A,D),(B,E),(B,F),(C,G),(D,H),(D,I),(G,J),(G,K),(H,L),(I,M),(I,N)}
这样的结点集合N和关系R反映了上述家庭的组成情况,形成该家庭组成的一种抽象描述,也就是一棵树。
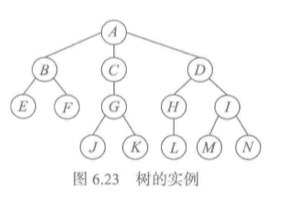
上述描述不太直观,可以使用文氏图描述,也即是上面的图。还可以使用嵌套括号描述(前面使用tuple构建的二叉树)。
2、定义和相关概念
定义:一棵树是n个结点的有限集T,当T非空时满足:
- T中有且只有一个特殊结点r,它是树T的根。
- 除根结点之外的其余结点分为m个互不相交的非空有限子集T0,T1,...,Tm-1,每个集合Ti为一棵非空树,称为r的子树。
结点个数为0的树称为空树,一棵树可以只有根没有子树,这就是单结点的树,只包含一个根结点。
一棵树可能有多棵子树,在有序树中,每个结点的子树都有明确的顺序,可以成为第一棵子树,第二棵子树,....。在无序树中,一个结点的不同子树没有顺序关系。
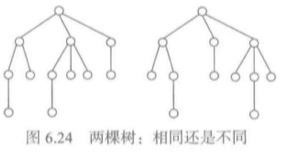
上图中,如果按照有序树,那么就是两棵不同的树,如果按照无序树就是相同的树。由于计算机表示中存在自然的顺序,所以数据结构里主要考虑的是有序树。
相关的概念
基本跟二叉树的类似。
有一点,二叉树中的子结点有明确左右之分,而有序树没有这个区分。因此,即使最大度数为2的有序树,跟二叉树也是比一样的。因为有序树没有左分支右分支的概念。
0棵或者多棵树的集合就是一个树林。
一棵空树就是一个空树林。如果树T非空,它可以分解为T=(r, F),其中r是树根,F是r的所有子树组成的树林。树和树林可以相互递归定义,非空树由树根及其子树树林构成,而树林由一组树构成。
对于树林也有有序树林和无序树林之分。
树、树林与二叉树的关系
有序树林跟二叉树存在一一映射关系,可以把任何一个二叉树映射为有序树林,也可以把任何一个有序树林映射为二叉树。
树林到二叉树的映射:
- 顺序连接同一个结点的各个子结点(也就是兄弟结点),作为这些结点的右分支的边(也就是作为二叉树的右分支)。
- 保留每个结点到其第一个子结点的连接作为该结点的左分支,并且删除这个结点到它的其他子结点的连接。
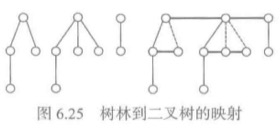
例子:上图。
二叉树到树林的映射:
- 对每个结点,在它与其左子结点的向右路径上的每个结点间加一条边。
- 删除原二叉树中每个结点向右路径上所有的边。
树的性质
跟二叉树类似
- 性质1:在度数为k的树中,第i层至多有k的i次方个结点。
- 性质2:度数为k,高为h的树中至多有
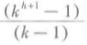 个结点。
个结点。 - 性质3:n个结点的k度完全树,高度h不大于logk(底)n的最大整数。
- 性质4:n个结点的树中有n-1条边。
3、抽象数据类型和操作


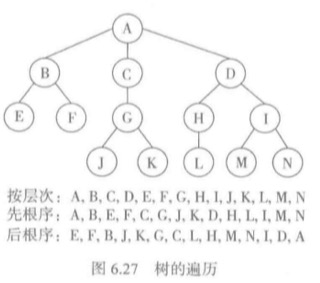
树的遍历
与二叉树一样,考虑遍历的时候,同样区分深度优先和宽度优先,并且深度优先有多种不同的遍历顺序。
实际上,在一般状态空间搜索问题上,搜索过程中经历的状态和状态之间的转移关系形成了一棵树,称为搜索树。
4、树的实现
树的表示有几种方法:
- 子结点引用表示法,父结点引用表示法。
- 子结点表表示法
- 长子-兄弟表示法
子结点引用表示
树的最基本表示方法就是子指针表示法,设计与二叉树的连接表示法类似:用一个数据单元表表示结点,通过结点间的链接表示树结构。但是有一个问题,树的度数不定。一种简单的考虑是只支持度数不超过固定m的树。
这样结点数据就是下图的布局。
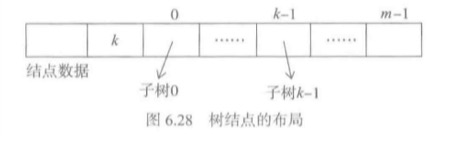
子结点引用表示的
- 缺点:是会出现大量空闲的结点引用域。在m度结点表示的n个结点的树中,恰好有n*(m-1)个空树引用域。
- 优点:能直接反映树的结构,操作灵活。
父结点引用表示
在任何树形结构里,除了树根之外的每个结点都有且只有一个父结点,利用这点,在子结点里记录与父结点的关系,那么每个结点就只需要一个引用域。但是仅仅这样,并不能组成唯一的树,因此,还需要利用一个顺序表来这样表示树,每个表元素对应于一个结点,这个结点包含两部分:结点数据和父结点的引用(父结点的下标)。
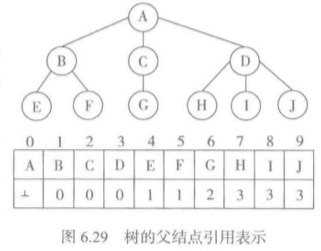
父结点引用表示的
- 优点:存储开销小,除了结点信息之外,每个结点只需要一个父结点引用域,对n个结点的树,需要O(n)的附加空间,与树的度数无关。
- 缺点:由于结构中只记录了父结点的关系,因此要想从父结点找到子结点,就必须通过查找过程,复杂度是O(n)。
子结点表表示
这种技术是用一个连续表存储树中各个结点的信息,每个结点关联一个字结点表,记录树的结构。其中子结点表使用链接结构实现。
这种表示中有两个单元
- 一种是表示结点,是结点数据和自己诶单表头指针的二元组
- 子结点表的结点单元。
采用子结点表表示,每个结点需要一个子结点引用域,每条边需要一个表结点。
长子-兄弟表表示
其实就是树的二叉树表示。采用这种表示,每个树结点对应于二叉树的一个结点。二叉树中结点d的左子结点是原树中d的第一个子结点,而二叉树中d的右子结点是原树中d的下一个兄弟结点。
5、树的python实现

class SubtreeIndexError(ValueError): pass def Tree(data, *subtrees): return [data].extend(subtrees) def is_empty_tree(tree): return tree is None def root(tree): return tree[0] def subtree(tree, i): if i < 1 or i > len(tree): raise SubtreeIndexError return tree[i+1] def set_root(tree, data): tree[0] = data def set_subtree(tree, i, subtree): if i < 1 or i > len(tree): raise SubtreeIndexError tree[i+1] = subtree

class TreeNode: def __init__(self, data, subs=[]): self.data = data self.subtrees = list(subs) class Tree: def __init__(self): self.root = None def is_empty_tree(self): return self.root is None def root(self): if self.is_empty_tree(): raise ValueError('the tree is empty') return self.root.data def subtree(self, i): if i >= len(self.root.subtrees): raise SubtreeIndexError return self.root.subtrees[i] def set_root(self, data): self.root = TreeNode(data, self.root.subtrees) def set_subtree(self, i, subtree): if i >= len(self.root.subtrees): raise SubtreeIndexError self.root.subtrees[i] = subtree




