字符串
目录
- 一、字符集、字符串和字符串操作
- 二、字符串的实现
- 三、字符串匹配(子串查找)
- 四、字符串匹配问题
- 五、python的正则表达式
- 六、部分课后编程练习
一、字符集、字符串和字符串操作
字符集就是一组字符组成的集合。例如:ASICC集合,Unicode集合。
基于字符串处理需要,要求字符集上有一种确定的序关系,称之为字符序。
字符串是一类特殊的线性表,表中的元素取自于选定的字符集,
1、字符串的相关概念
- 字符串的长度。字符个数。
- 字符在字符串中的位置,与线性表一样,用下标表示。
- 字符串相等。长度相等,并且两个字符在字符集里一一相等。
- 字典序。从左往右,比较两个字符串,下标相同的第一对不同字符的比较作为字符串比较的结果。如果都相同,那么较短的一个字符串比较小。
- 字符串拼接。'1'+2' 为'12'
- 子串关系。 s = s1+s2。那么s1和s2都是s的子串。可以为空。
- 前缀和后缀。s = s1+s2。那么s1是s的前缀。s2是s的后缀。
2、字符串抽象数据类型

最后两个操作是变动操作,如果将字符串定义为不变的数据类型,那么可以生成另外一个字符串对象,如果是可变的数据类型,那么实际修改本字符串即可。
二、字符串的实现
1、基本实现问题和技术
问题1:采用哪种方式实现顺序表
解决:如果要设计可变类型的字符串,就使用必须分离式顺序表的形式。如果设计不变类型的字符串,可以采用一体式顺序表设计。
问题2:如何设计字符串的存储
解决:把一个字符串的字符序列存储在一组存储块里,并链接起这些存储块。
问题3:字符串结束的表示
解决:用一个num记录字符串的长度(python)。或者用一个特殊字符表示字符串的介绍(c语言)。
字符串的操作实现跟连续表中很多都相似。但也有自己独特的性质,字符串通过是作为一个整体来看的。还有字符串串匹配是这章主要研究的方向。
2、实际语言中的字符串
从略,详情看书。
3、python的字符串
python的字符串类型是不变的数据类型,因此它采用的一体式顺序表形式。

str的操作
- 解析操作。也就是获取str对象的信息。长度,检查是否全部为数字。获得某个下标的字符。
- 构造操作。基于str对象构造新的str对象。切片、大小写复制,各种格式化。切分操作split,replace,等。
str操作的实现
- O(1)时间的简单操作。包括串的长度len和定位访问字符的解析操作。
- 其他操作都需要扫描这个串的内容。包括(in,not in, max/min),各种字符串类型判断(是否全为数字等),这些操作都需要通过一个循环逐个检查传中字符才能完成工作,因此都是O(n)时间的操作。
以切片操作为例,说明一下。
切片操作s[a,b,k]的算法应该是:
- 根据a,b,k的值和s的长度计算出新字符串的长度。分配存储。
- 用一个形式为for i in range(a, b, k)...的语句逐个把s[i]复制到新的字符串的各个位置。
- 返回这个新建的字符串。
三、字符串匹配(子串查找)
1、字符串匹配
假设有两个字符串。t=t0 t1 t2 t3....tn-1。 p=p0 p1 p2 p3....pm-1。字符串匹配就是在t中查找与p相同的子串的操作。
例如:s1 = 'qwertyu' s2='yu'。那么s2就能匹配到s1。由于字符串可能非常大,所以匹配的算法的效率非常重要。
2、串匹配和朴素匹配算法
如果从目标串的某个位置i开始,模式串里的每个字符都与目标串里的对应字符相同,就是找到了一个匹配。
因此,串匹配算法设计的关键有两点:
- 怎样选择开始比较的字符对。
- 发现不匹配之后,下一步怎么做。
朴素的串匹配算法
最简单的朴素匹配算法采用的直观可行的策略:
- 从左到右逐个字符匹配。
- 发现不匹配,转去考虑目标串中的下一个位置是否与模式串匹配。


def native_match(t, p): m, n = len(t), len(p) i, j = 0, 0 while i < m and j < n: if t[i] == p[j]: j += 1 i += 1 else: i = i-j+1 j = 0 if j == n: return i-j return -1
上面算法很简单,非常容易理解,但是效率极低。造成效率低的最主要原因是执行中出现了回溯。最坏的情况,这个算法的复杂度需要O(m*n)。
3、无回溯匹配算法(KMP算法)
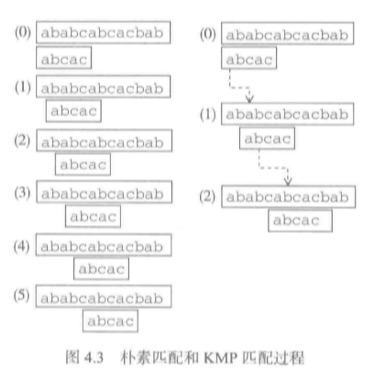
kmp是一个高效的算法,用一个例子来解释一下。
t(目标串)=ababcabcacbab。
p(模式串)=abcac
在上图中,如果是朴素匹配算法,要经过5步才能到达最后一个结果,但是kmp只需两部就可到达。
具体执行过程分析:
- 状态0。匹配到模式串c时失败。但是,此前有两个字符(ab)匹配成功,由此推出,模式串和目标串的前两个字符一一相同。也就是t1=p1,t2=p2。
- 状态1。在朴素算法里,目标串发生回溯,回到字符b。模式串从字符a开始匹配。但是在kmp算法没有这一步,那是因为kmp算法利用了上一步得出的结论,推出这一步没必要比较(因为t1=p1,t2=p2,而且p1!=p2,因此p1!=t2)。
- 状态2。模式串中前四个字符都匹配(abca),最后一个字符不匹配(c)。得出t3=p1,t4=p2,t5=p3,t6=p4。
- 状态3。未利用上面信息,发送回溯。但是kmp算法是利用了上面的信息,从p1!=p2!=p3得出t3!=t4!=t5。因此p1!=t4!=t5。所以状态3和状态4。kmp算法就没有进行匹配。直接从p1跟t6开始比对。也就到达了最后一步。
- 状态4。未利用上面信息,发送回溯。
- 状态5。朴素算法到达最后一步。
通过这个例子可以看出kmp算法的精髓就是开发了一套分析和记录模式串信息的机制(和算法),而后借助得到的信息加速匹配。
问题分析
kmp算法的基本思路是匹配中不回溯。在匹配失败时,把模式串前移若干位置,用模式串里匹配失败字符之前的某个字符与目标串中匹配失败的字符比较。
要实现这种策略,关键在于确定匹配失败时模式串如何前移。这里考虑用一个长为m的表pnext,表中的元素,就记录着要模式串要返回的字符串的下标值。
这里还有一种特殊情况,在匹配一些pj失败的时候,发现前面模式串跟目标串匹配没有实际价值,那么就在pnext存入-1。很明显,pnext[0] = -1。也就是当模式串的第一个字符进行匹配的时候,前面没有任何可以借鉴的信息。
那么现在假设已经做出了pnext,那么就很容易得出kmp的匹配算法。

def kmp_match(t, p, pnext): m, n = len(t), len(p) i, j = 0, 0 while i < m and j < n: if j=-1 and t[i] == p[j]: j, i = j+1, i+1 else: j = pnext[j] # 回到那个pnext中存入的值。从新匹配 if i==m: return j-i return -1
因为是无回溯,在匹配过程中t的指针i,一直是向前的,所以,这个算法的复杂度是O(n)。
构造pnext表:分析
通过上面的分析跟例子可以得出两点:
- 模式串移动之后,作为下一个用于匹配字符的新位置,其前缀子串应该与匹配失败的字符之前同样长度的子串相同。
- 如果满足上述条件不止一处,那么只能做最短的移动,即将模式串移动到离它最近的那个下标的位置。

现在要计算位置i的前后缀相等的最长长度。假设这时候pnext[i-1]已经计算出来结果,为k-1。那么i位置的结果就只有两种情况:
- pk=pi的时候,那么最长距离加一。pnext[i] = k
- pk!=pi的时候,那么退回到最短的相同前缀,然后继续向前检查。

def gen_penxt(p): i, k, m = 0, -1, len(p) pnext = [-1] * m while i < m-1: if k == -1 or p[i] == p[k]: i, k = i+1, k+1 pnext[i] = k else: k = pnext[k] #退回到更短的相同前缀继续检查
这个算法复杂度是O(m),分析跟kmp算法复杂度的分析类似。
KMP算法的时间复杂度
KMP整个算法时间复杂度,既包括pnext表的生成,还包括,匹配的算法。因此整个复杂度是O(m+n)。通常情况下,m远小于n,因此可以认为这个算法复杂度为O(n),显然要优于朴素算法的O(m*n)。
注意KMP算法的应用场景,它比较适合一个模式串在多个目标串中匹配的情况。因为模式串的pnext生成只需要做一次,这样即使目标串很多,也能速度很快。这是最适合KMP算法的场景。
四、字符串匹配问题
1、串匹配/搜索的不同需要
在实际生活中人们可能需要查找的不是某个固定的字符串,而是很多特殊的字符串,比如:一个文本中所有双引号括起来的词语,包含"数据结构"的数据等等。
要想处理这类字符串匹配问题,就需要考虑字符串集合的描述,以及对于是否属于一个字符串集合的检查。
模式、字符串和串匹配
一个模式描述了一些字符串的集合。前面讨论的字符串匹配问题,都是模式的一个特例,即模式的形式就是一个普通字符串。
但更多的情况,模式是一个字符串的集合,也就是说它的模式串可能不只一个。比如:前面的例子,匹配括号中所有的词语。那么模式串就可能有很多个,只要符合在括号中这个要求,就是模式串。
为了研究这个情况,就需要对模式有个严格的描述。并且要实现高效匹配。
通配符和简单模式语言
在文件名的描述中,可以使用通配符'*'和'?'。其中星号表示可以与任意一串字符匹配,?表示可以与任意一个字符匹配。
那么在普通字符串的基础上加上通配符,就形成了一种简单的模式描述语言。例如a*就表示了以a开头的所有字符串。
不过,仅仅加入了通配符的膜还是语言不够灵活,描述能力不强,能描述的字符串集合很有限。
正则表达式
一种非常有意义的模式语言是正则表达式。
2、一种简化的正则表达式
这里考虑一种比较简单规则的正则表达式的匹配机制。
用以下符号描述:
- 任一字符都与自身匹配。
- 圆点符号'.'可以匹配任意字符。
- 符号'^'只匹配目标串的开头,不匹配任何具体字符。
- 符号'$'只匹配目标串的结束,不匹配任何具体字符。
- 符号'*'表示其前面那个字符可匹配0个或者1个。
匹配算法

def match(re, text): def metch_here(re, i, text, j): ''' 检查从text[j]开始的正文是否与re[i]开始的模式匹配 ''' while True: if i == rlen: return True if re[i] == '$': return i+1 == rlen and j == tlen if i +1 < rlen and re[i+1] == '*': return match_star(re[i], re, i+2, text, j) if j == tlen or (re[i] != '.' and re[i] != text[j]) return False i, j = i+1, j+1 def match_star(c, re, i, text, j): ''' 在text里跳过0个或者多个c后检查匹配 ''' for n in range(j, tlen): if match_here(re, i, text, n): return True if text[n] != c and c!= '.': break return False rlen, tlen = len(re), len(text) if re[0] == '^': if match_here(re, 1, text, 0): return 1 for n in range(tlen): if match_here(re, 0, text, n): return n return -1
五、python的正则表达式
1、概况
python正则是用字符串字面量的描述形式,也就是'-'形式描述的,因此它们看起来就是普通的字符串。只是在用于re包的操作时,把它当做一个字符串模式处理。
2、基本情况
原始字符串
原始字符串就是在普通字符串前面加r或者R。例如:r'abc'。它跟普通字符串有一点不同就是'\'不作为转义符。
因此,如果要写正则表达式,用原始字符串写的话,可能是r'C:\course\python',用普通字符串的话因为需要转义,所以是'C:\\course\\python'。
元字符(特殊字符)
正则表达式re规定了14个特殊字符:
~$[]{}().*?\+|
3、主要操作
- 生成正则表达式对象:re.compile(pattern, flag=0)。本操作生成与之对应的正则表达式的对象。如果一个模式串需要反复使用,那么可以先用compile生成正则表达式并计入变量。
- 检索:re.search(pattern, string, flag=0)。在string中检索与pattern匹配的子串。找到返回一个match类型的对象。否则返回None。
- 匹配:re.match(pattern, string, flag=0)。检查string是否存在一个pattern匹配的前缀。匹配成功返回match对象,否则返回none。
- 分割:re.spilt(pattern, string, maxsplit=0, flags=0)。以pattern作为分割串将string分段。参数maxsplit指明最大分割数,用0表示要求处理完整个string。函数返回分割得到的字符串的表。
- 找出所有匹配串:re.findall(pattern, string, flags=0)。返回一个表,表中元素是按照顺序给出的string里与pattern匹配的各个子串。
4、正则表达式的构造
字符组
1>、字符组描述符[...]
描述一组字符的表达式用[...]。表示与方括号内所有的字符序列中的任意一个字符匹配。字符组的字符排列顺序不重要。
在字符组方括号内的形式:
- 逐一列出的字符序列。例如:[abc]可以与a或b或c匹配。
- 采用区间形式表示。例如:[0-9]可以与0到9的任意一个字符匹配。
- 特殊形式[^]。例如:[^0-9]匹配非十进制数字的所有字符。
2>、圆点字符
圆点是通配符,它能匹配任何字符。例如:a..b能匹配所有以a开头以b结尾的字符串。
为了方便re还采用转移的形式定义了一些常用字符组。
- \d表示[0-9]
- \D表示[^0-9]
- \s表示[\t\v\n\f\r],与所有空白字符匹配
- \S表示[^\t\n\v\f\r],与所有非空白字符匹配
- \w表示[0-9a-zA-Z],与所有字母数字匹配
- \W表示[^0-9a-zA-Z],与所有非字母数字匹配
重复
1>、重复描述符
*,表示能匹配前一个字符0次或者多次。
+,表示能匹配前一个字符1次或者多次。
2>、可选描述符
?是可选描述符,表示0次或1次。例如:a?可以匹配空串或者a。
3>、重复次数描述符
用{n}表示重复次数的描述符。例如a{3},可以匹配aaa。
4>、重复次数范围的描述符
使用{m,n}表示串的m到n次重复,包括m次和n次。例如:a{2,5}可以匹配aa,aaa,aaaa,aaaaa四个字符。
重复匹配都有一个问题,如果可以匹配0次或多次,那么该返回哪种情况呢?
例如:re.search('a*', 'aabba'),返回的match对象是a呢,还是aa呢?
这里就设计到正则匹配的两种模式:
- 贪婪模式。模式与字符串里有可能匹配的最长子串匹配。在上面的例子中就是返回aa。
- 非贪婪模式。模式与可能匹配的最短子串匹配。在上面例子中就是返回a。
对于*,+,?,{m,n}默认都是贪婪模式的。因此上面的例子中返回的是aa的mach对象。即匹配最长的子串。
如果要改变为非贪婪模式,就需要在其后面加上?。那么这样*?,+?,??,{m,n}?就是非贪婪匹配了,表示匹配最短的字符。
选择
1>、选择描述符
用|表示两种或者多种情况匹配。例如:a|b|c可以匹配a或者b或者c。(ab)|(bc)表示可以匹配ab或者bc。
注意一点|的结合力最弱,也就是说它的优先级最低,比顺序组合的结合力还弱,因此需要使用圆括号来增强结合力。
首尾描述符
1>、行首描述符。'^'
2>、行尾描述符。'$'
注意一点,如果串里有换行符,那么包括换行符前的子串的后缀和换行符后子串的前缀。
例如:re.match('^for', 'books\nfor children')将匹配成功。
re.match('ren$', 'children\nbooks')也匹配成功。
3>、串首描述符。
\A开头的模式只与整个被匹配串的前缀匹配。
\Z结束的模式只与整个被匹配串的后缀匹配。
单词边界
\b描述单词边界,在实际单词边界位置匹配空串,也就是非字母数字的字符或者无字符(串的开头/结束)。
还有一个问题,\b在python字符串中表示退格符,因此为防止歧义,在使用字面量方式的正则模式中要使用转义字符,或者直接使用原始字符来写正则模式的字符串。
例如:'\\b(0+|[1-9]\d*)\\b'也可以写成r'\b[0+|[1-9]\d*)\b]'

# 匹配一个python程序里出现的所有整数之和 def sumInt(fname): re_int = r'\b(0|[1-9]\d*)\b' # 因为整数第一位不能为0。 f = open(fname) if f == None: return 0 int_list = map(int, re.findall(re_int, f.read())) num = 0 for n in int_list: num += n return num
\B是\b的补,表示在相应位置是字母或者数字,也可以匹配空串。
match对象
search,match等方法如果匹配成功都是返回的match对象。匹配不成功返回None。
- 取得被匹配的子串。mat.group()
- 在目标串里的匹配位置。mat.start()
- 目标串里被匹配子串的结束位置。mat.end()
- 目标串里被匹配的区间。mat.span()
- mat.re取得正则表达式对象。
- mat.string取得目标串。
模式里的组(group)
用()括起来的模式段就是一组。在一次成功匹配之后,模式串的各个组也都成功匹配,与它们匹配的一组字符串从编号1开始,通过方法mat.group(n)获取。
并且模式里各个圆括号确定的组按开括号的顺序编号。例如:
mat = re.match('.((.)e)f', 'abcdef')
mat.group(1)是de,mat.group(2)是d。mat.groups()得到('de', 'd')
组还有一个用处,就是匹配应用前面的成功匹配,建立前后的部分匹配之间的约束关系。在模式串后面用\n的形式表示,其中n是一个整数。
例如:r'(.{2}) \1'可以匹配'ok ok'、'no no',不能匹配'ok no'。
其他匹配操作
- re.fullmatch(pattern, string,flags=0)
- re.sub(pattern, repl, string, count=0, flags=0)
- re.finditer(patter,string, flags=0)
正则表达式对象
可以使用正则表达式的对象直接匹配。
- regex = re.compile(pattern)生成正则表达式对象。
- regex.match(string,[pos,[endpos]])
- regex.search(string,[pos,[endpos]])
- regex.findall(string,[pos,[endpos]])
六、部分课后编程练习

# 针对Python的str对象,自己实现一个replace操作函数 def replace(self, str1, str2, count=-1): m, n = len(str1), len(self) i, j = 0, 0 pnext = MyStr.gen_pnext(str1) aftstr, a, b ='', 0, -m while j < n: if i == m: a, b = b+m, j-i aftstr += self[a:b] + str2 i, j= 0, j+1 if i == -1 or str1[i] == self[j]: i, j = i + 1, j + 1 else: i = pnext[i] aftstr += self[b+m:] return aftstr

""" 定义生成器函数tokens(string,seps),其中string参数是被处理的字符串,seps是描述分隔字符的字符串, 都是str类型的对象。该生成器逐个给出string里一个个不包含seps中分隔字符的最大子串。 """ def tokens(self, seqs): m, n = len(seqs), len(self) i, j = 0, 0 pnext = MyStr.gen_pnext(seqs) a, b = 0, -m while j < n: if i == m: a, b = b + m, j - i yield self[a:b] i, j = 0, j + 1 if i == -1 or seqs[i] == self[j]: i, j = i + 1, j + 1 else: i = pnext[i] yield self[b + m:]

""" 请基于链接表的概念定义一个字符串类,每个链接结点保存一个字符。实现其构造函数(以python的str对象为参数)。 请定义下面方法:求串长度,完成字符串替换,采取朴素方式和KMP算法实现子串匹配。 """ class LStr: @staticmethod def gen_pnext(p): i,k,m = 0, -1, len(p) pnext = [-1]*m while i < m-1: if p[k] == p[i] or k == -1: i, k = i+1, k+1 pnext[i] = k else: k = pnext[k] return pnext def __init__(self, str): self._head = None print(len(str)-1) for i in range(len(str)-1, -1, -1): self.prepend(str[i]) def prepend(self, elem): self._head = LNode(elem, self._head) def printall(self): p = self._head while p is not None: print(p.elem) p = p.next def __len__(self): p, i = self._head, 0 while p is not None: p = p.next i += 1 return i def search(self, i): if i<0 or i>= self.__len__(): print(self.__len__()) raise ValueError p, e = self._head, 0 while p is not None and i>=0: e = p.elem p = p.next i -= 1 return e def match(self, p): m, n = len(p), self.__len__(), i, j = 0, 0 while i<m and j<n: if self.search(j) == p[i]: i, j = i+1, j+1 else: i, j = 0, j-i+1 if i == m: return j-i return -1 def print_a_b(self, a, b): p = self._head s = '' while p is not None and b>0: if a<=0: s += p.elem a, b = a-1, b-1 p = p.next return s def KMP_match(self, p): m, n = len(p), self.__len__(), i, j = 0, 0 pnext = LStr.gen_pnext(p) while i<m and j<n: if i == -1 or self.search(j) == p[i]: i, j = i+1, j+1 else: i = pnext[i] if i == m: return j-i return -1 """ 这个函数可以优化,因为链表可以修改其中的结点,所以完全不必要重新创建一个字符串来存替换后的字符串。只需要在原链表上进行替换就可以。 """ def replace(self, str1, str2, count=-1): m, n = len(str1), len(self) i, j = 0, 0 pnext = LStr.gen_pnext(str1) aftstr, a, b ='', 0, -m while j < n: if i == m: a, b = b+m, j-i aftstr += self.print_a_b(a, b) + str2 i, j= 0, j+1 if i == -1 or str1[i] == self.search(j): i, j = i + 1, j + 1 else: i = pnext[i] aftstr += self.print_a_b(b+m, n) return aftstr def find_in(self, another): if not isinstance(another, str): raise TypeError p,i = self._head,0 while p is not None: if p.elem in another: return i i += 1 p = p.next def find_not_in(self, another): if not isinstance(another, str): raise TypeError p,i = self._head,0 while p is not None: if p.elem not in another: return i i += 1 p = p.next def remove(self, another): if not isinstance(another, str): raise TypeError p, q = self._head, None while p is not None: if p.elem in another: if p == self._head: self._head = self._head.next else: q.next = p.next #这里q都不必要变。 else: q = p p = p.next

""" 为上述链接表字符串类增加下面的方法: 1、find_in(self, another),确定本字符串中第一个属于字符串another的字符所在结点的位置,返回表示这个位置的整数。 2、find_not_in(self, another),与上面函数类似,但它要查找的是不属于another的字符。 3、remove(self, another),从self里删除串another里的字符 答案: 见上面的find_in函数和find_not_in函数和remove函数 """




