POJ3700：寻求最优搜索方法

     最近沉迷于算法研究中，被POJ上ID为3700的这道题折磨了两天后，终于顺利通过了。深深震撼于程序性能因搜索方法的不同而产生的天壤之别。

     该题描述如下：给出一组互不相同的整数，求可将其划分为递变（递增或递减）序列的最少个数。例如：给出5个数3，5，2，4，1，最少可将其划分为2个序列。第一个序列为3，4，第二个序列为5，2，1。

     我首先想到用多叉树逐层计算。每个节点存放一个数组a, a中保存还未划分的原始数据，扩展该节点时，遍历a,找出所有以a[0]为首的递变序列，每找到一个递变序列，就为该节点增加一个子节点，并将a中剩余的数据存放到该子节点中。这样每个节点可能会有多个子节点。逐层扩展，当某个节点无法扩展时，所有的数据就划分完毕，这个节点的层数就是这种划分方式的序列个数。

     我尝试用广度优先扩展构造树。因为仅需要得到一个无法扩展的节点，就可以退出计算。提交了第一个版本，结果MLE(memory limit exceed)。稍微修改下，将节点中静态分配的内存改为动态的按需分配，第二个版本TLE(time limit exceeded)。我估计在数据量很大时，每个节点的子节点都很多，造成同一层上需要计算的节点数量太大而导致超时。 于是我改为深度优先扩展，再加些判别条件用于剪枝。第三个版本，依然TLE。

    难道是算法本身的问题？我从POJ的讨论组中找到一个通过的版本，用贪心法加DFS,大致思想如下：

• 　　每个数要么跟随一个上升序列，要么跟随一个下降序列。（DFS）
• 　　如果要跟随上升（下降）序列，则跟末尾数最大（小）的那个。（贪心思想）
• 　　在无法跟随已有的上升（或下降）序列时，则新开一个上升（或下降）序列。

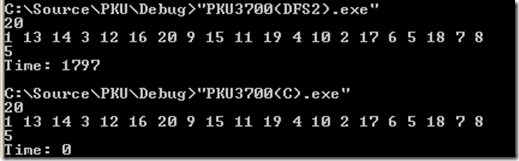
     依据此思想我写了第四个版本，终于顺利通过了。欣喜之余，我比较了一下此方法和前面超时的第三个版本在性能上的差异。我用了20个输入数据，比较结果如下：

 

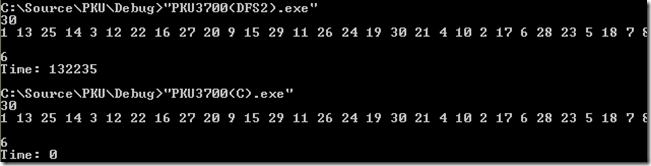
     版本三用了1797ms,而版本四用了0ms(小于1ms)。 速度差异至少千倍。然后我用30个数据测试，结果如下：  

     这个结果让我非常震惊：版本三用了132235ms （难怪TLE）,而版本四仍然用了0ms。速度差异达到数十万倍。同样是dfs, 其实这两个版本的主要差别是搜索方法的不同。思考了良久，粗浅的发现了以下2个原因：

• 　　版本四考虑将每个数据或置于上升序列，或置于下降序列，实际上构成一颗满二叉树。而版本三是子节点数目不定的多叉树。从遍历效率上看，二叉树优于多叉树。
• 　　版本三在构造树节点时效率太低。每次将一个节点中的所有数据遍历一遍之能生成一个子节点，这样同样一组数据要反复遍历多次才能生成所有子节点。 而版本四在构成新节点时，只需和所有已划分序列的最大（最小）值比较一遍即可。

     为解决大量的数据处理问题，我们学了很多算法，往往都是为了找到一个最优的搜索方法。这种搜索方法因具体问题而异。需要我们在做题中积累经验并且善于归纳、联想、对比来确定最优方案。这个最优方案往往会使程序性能有超乎想象的提高。