Codeforces Round #557 (Div. 2)

http://codeforces.com/contest/1162

a.pass

b.给两个相同形状矩阵a，b，ab之间可以的对应位置的值可以互换。问：能否通过互换来是a和b均分别满足条件p：每行严格单调增，每列严格单调增。

证明：

严谨地说，条件p依赖于矩阵每个值，因此是有指数级别的可能矩阵的。我们需要证明这个整体性质是局部性质的简单相加，俩俩元素间满足，然后最终整体也满足。对于位置x(i,j)和位置y(i+1,j)而言，x位置在a上是xa，在b上是xb，y同理。

那么当min(xa,xb)>=max(ya,yb)那么无论如何最终目标都无法形成。那么是否所有位置都满足min(xa,xb)<max(ya,yb)就可以产生解呢？不是的。要在a和b上分别满足此条件，那么我们要凑出一个xa<ya && xb<yb 的情况其实就是min(x)<min(y) && max(x)<max(y)，整体性质在这种安排下没有矛盾，因为我们恒把min留在a，把max放在b。在这种安排下，任一位置不满足条件的话，再怎么安排都不会满足。这样子构造性证明来的容易的多。

c.题目：我们有一个m长度的整数array，m>2，m的两端值是0，中间每个数1<=mi<=n，然后我们在给m涂色，颜色有1-n可选，规则：先先两个相邻的颜色值比如i和i+1，然后给m分成两段，前面两颜色之一，后面涂另一种。问：有多少种涂色顺序使各点颜色x与值y均满足x!=y，就是对于每个点，他的值和颜色不能相等。注意：我们值关心涂色顺序，从i变i+1的位置我们不关心。

因为颜色值必须相邻的设定，导致可选规则很有限（o(n)级别），那么问题的切入点是给定一种涂色顺序，问能调整变色位置否达到要求。很容易找到充要条件：对涂色顺序x->y来说，如果某x值出现晚于y值，那么肯定不行，否则肯定行。怎么实现？你会发现我们只关心x最晚出现位置是否大于y最早出现位置，那么对每个值记录其最早最晚出现位置不就能快速查询了。然后遍历解空间，逐个判断即可。

d.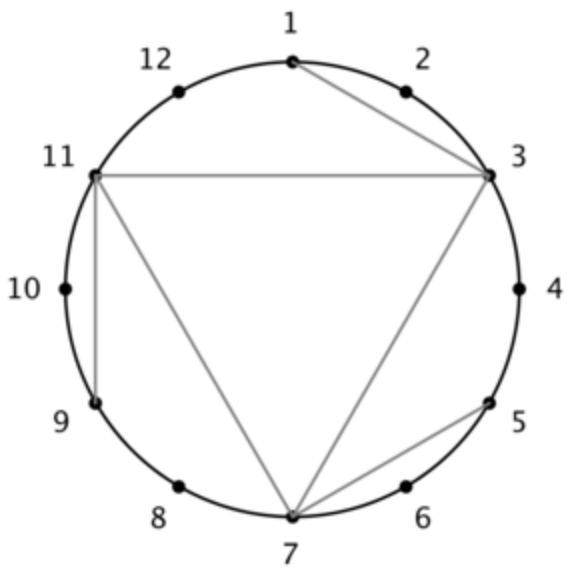

给一个数字n，意味着这个‘钟表’的圈的大小，普通钟表n=12。然后给m对数(x1,y1)->（xm,ym），表示有线连接xi于yi，问能否旋转一个角度（!=2pi）使图形不变。

问题切入点：我们可以按照连线长度把连线分组，长度1的一组，2的一组.....，只记录开始位置，因为已经与结束位置无关了。然后分别找最小旋转角度，然后这些最小旋转角度的最小公倍数如果是小于n的，这个角度就是公共的最终旋转角度。

那么实现的时候，按照长度划分完了，怎么求这些起点的最小旋转角度呢？把他们首尾连线，这样就是一个新的问题了，递归去做就好了。递归终点：只有一种长度，这个长度就是最小旋转角度！乱七八糟写了一通，竟然a了。。我感觉这个思路必然不是最优解。

 e.有2n堆石头堆，ab两个人轮流操作：先选其中n堆，再从选中的n堆中每堆拿出任意多石头扔掉。谁选不到n堆（剩下有石子的堆数不足n）时，就输了。a先b后，该游戏的特点：假如两人足够聪明，是 没有任何游戏性可言的，因为当前堆石头的样子决定了ab中某一人按照最优方法去玩会必胜。给定石头堆 2n，以及各堆数量找到这个规律，确定谁会必胜。

从游戏最后一手往前递推，找到游戏模式，最终答案是0(n)的。

最后一手是玩家x发现当前堆不足n，那么我们发现当前堆不足2n的时候，我们直接拿空n堆，导致对方lose。但是当前有2n堆的话我们怎么拿？我们至少知道了不能拿空任何一堆，因为这会导致对方会拿空n堆让我们lose。什么情况下我们会递推到之前结论呢？就是某些堆的石子数量是1的时候，我们没得选，只能拿空？而其他情况再由后续讨论。当数量为1的石子堆数量大于n的时候，我们不得已会拿空某一或某些堆，从而导致对方胜利，但是数量1石子堆数<=n呢？假如存在数量1石子堆数，我们就使其他的n堆也转化称数量1的，这样对方lose。假如不存在数量1的，而假设数量2的有x堆，那么。。。。画一个2维表格，以此类推，容易得到最终解：我们的目标是一致维持最少石子堆的数量>=n。我们如果能在第一步做到的话，那么我们可以在以后的任一步做到这一点。最后导致胜利。✌️