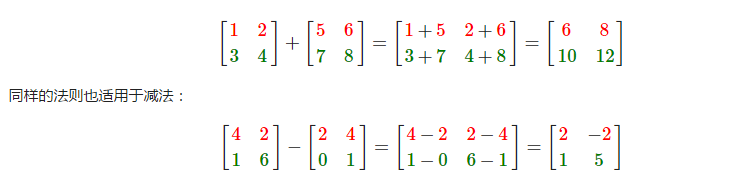变换
使用(多个)矩阵(Matrix) 对象可以更好的变换(Transform)一个物体。
向量
向量最基本的定义就是一个方向。
或者说 向量有一个方向(Direction)和大小(Magnitude,也叫做强度或长度)。
向量可以在任意纬度(Dimension)上 ,但是我们通常只使用2至4维。
如果一个向量有两个纬度,它表示一个平面的方向(想象一下2D的图像),当它有3个纬度的时候它可以表达一个3D世界的方向。
下面图片会看到3个向量,每个向量在2D图像中都用一个箭头(x,y)表示。我们在2D图片中展示这些向量,因为这样子会更直观一点。
你可以把这些2D向量当做z坐标为0的3D向量。
由于向量表示的是方向,起始于何处并不会改变它的值。
下图我们可以

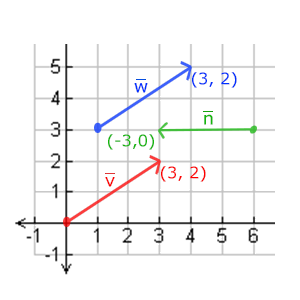

由于向量是一个方向,所以有些时候会很难形象地将它们用位置(Position)表示出来。
为了让其更为直观,我们通常设定这个方向的原点为(0,0,0),然后指向一个方向,对应一个点,使其变为位置向量(Position Vector)
也可以把起点设置为其他的点,然后说:这个向量从这个点起始指向另一点)。比如说位置向量(3,5)在图像中的起点会是(0,0),并会指向(3,5)。
我们可以使用向量在2D或3D空间中表示方向与位置。
向量与标量运算
标量(Scalar)只是一个数字(或者说是仅有一个分量的向量)。
当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。
对于加法来说会像这样:
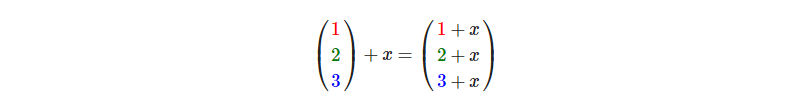
其中的+可以是+、-、.或÷,其中 . 是乘号。注意- 和 ÷ 运算时不能颠倒(标量 -/÷ 向量),因为颠倒的运算是没有定义的。
向量取反
对一个向量取反(Negate)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。
我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
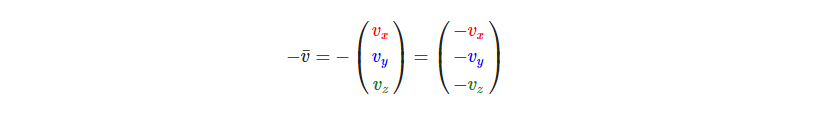
向量与向量加减
向量的加法可以被定义为是分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量:
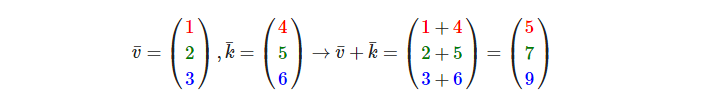
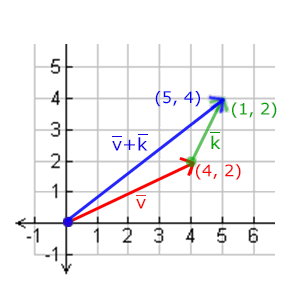
向量v = (4,2)和k =(1,2)可以直观地表示为:
就像普通数字加减一样,向量的减法等于加上第二个向量的相反向量:
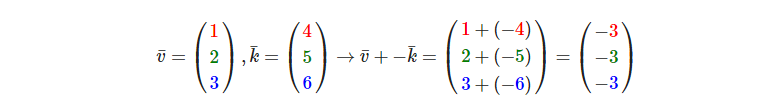
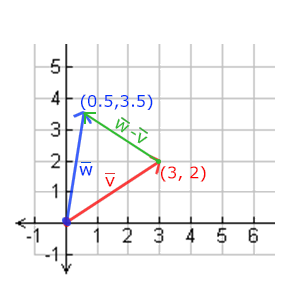
两个向量的相减会得到这两个向量指向位置的差。这在我们想要获取两点的差会非常有用。
长度
我们使用勾股定理(Pythagoras Theorem) 来获取向量的长度(Length)/大小(Magnitude)。
如果把向量的x与y分量画出来、该向量会和x与y分量为边形成一个三角形:
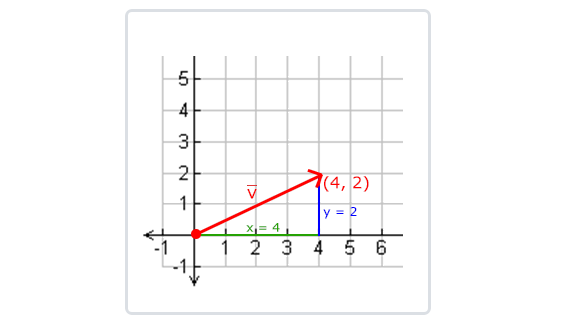
因为两条边(x和y)是已知的,如果希望知道 ,我们可以直接通过勾股定理来计算:
,我们可以直接通过勾股定理来计算:

有一个特殊类型的向量叫做单位向量(Unit Vector)。
单位向量一个特别的性质-------它的长度是1。
我们可以用任意向量的每个分量除以向量的长度得到它的单位向量。
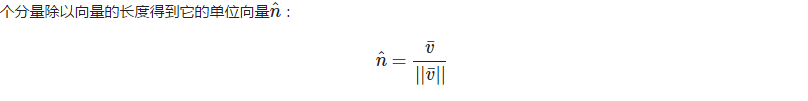
我们把这种方法叫做一个向量的标准化(Normalizing)。单位向量头上有一个^样子的记号。
通常单位向量会变得很有用,特别是我们只关心方向不关心长度的时候(如果改变向量的长度,它的方向并不会改变)。
向量相乘
两个向量相乘是一种很奇怪的情况。
普通的乘法在向量上是没有定义的,因为它在视觉上是没有意义的。
但是在相乘的时候我们有两种特定情况可以选择:

点乘
两个向量的点乘等于它们的数乘结果乘以两个向量之间的余弦值。下面是公式:

现在点积只定义了两个向量的夹角。
90度的余弦值是0,0度的余弦值是1。
使用点乘可以很容易测试两个向量是否正交(Orthogonal)或平行(正交意味着两个向量互为直角)。
如果想要多了解正弦或余弦函数的知识可以看教程:可汗学院的基础三角学视频。
也可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的长度之积,得到的结果就是夹角的余弦值
通过上面点乘定义式可推出:

所以,我们该如何计算点乘呐?点乘是通过将对应分量逐个相乘,然后再把所得积相加来计算的。
两个单位向量的点乘会像是这样:
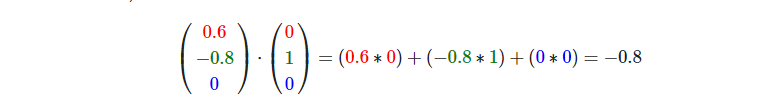
点乘会在计算光照的时候非常有用。
叉乘
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量。
如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。
下面图片展示了3D空间中叉乘的样子:
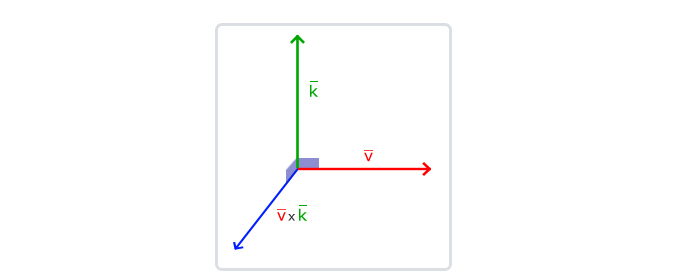
下面你会看到两个正交向量A和B叉积:

只要按照步骤来,就能得到一个正交于两个输入向量的第三个向量。
矩阵
简单来说矩阵就是一个矩形的数字、符号或表达式数组。
矩阵中每一项叫做矩阵的元素(Element)。
下面是一个2x3矩阵的例子:
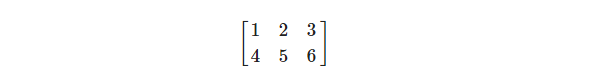
矩阵可以通过(i,j)进行索引,i是行,j是列,这就是上面的矩阵叫做2x3矩阵的原因(3列2行,也叫做矩阵的纬度(Dimension))。
这与你在索引2D图像时的(x,y)相反,获取4的索引是(2,1)(第二行,第一列)(注:如果是图像索引应该是(1,2),先算列、再算行)。
它就是一个矩形的数学表达式阵列。和向量一样,矩阵也有非常漂亮的数学属性。
矩阵有几个运算,分别是:矩阵的加法、减法和乘法。
矩阵的加减
矩阵与标量之间的加减定义如下:
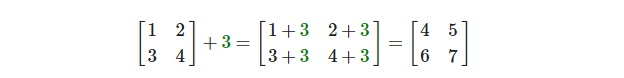
标量值要加到矩阵的每一个元素上。矩阵与标量的减法也相似:

矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算,所以总体的规则和与标量运算是差不多的,
只不过在相同索引下的元素才能进行运算。这也就是说加减法只对同纬度的矩阵才是有定义的。
一个3x2矩阵和一个2x3矩阵(或一个3x3矩阵与4x4矩阵)是不能进行加减的。
两个2x2矩阵是怎么相加的: