第三次作业

作业要求：https://edu.cnblogs.com/campus/hljkj/CS201802/homework/2360

第11周第6次作业：求平方根序列前n项和。

#include<stdio.h>
#include<math.h> 
int main(void)
{
 int n=0,i=1;
 double sum;
 scanf("%d",&n);
 for(i=1;i<=n;i++){
  sum=sum+sqrt(i);
 } 
 printf("sum = %.2f",sum);
 
 return 0;
}

解题思路：

1.定义变量i和n为整型，sum为双精度浮点型；

2.获取用户输入，将其赋值给n；

3.利用for语句完成sqrt(i)序列求和，满足循环条件则sum=sum+sqrt(i);要满足到n的平方根累和，则约束条件只能为i<=n或i<n+1；

4.输出sum，保留两位小数

 

流程图：

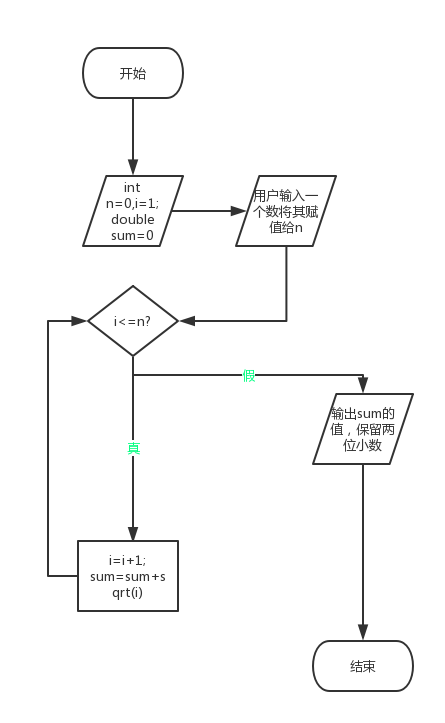
调试成功，循环语句还可以换成sum=sum+pow（i,1/2）

第十二周作业第9次作业：输出闰年

#include<stdio.h>
int main(void){
    int n,i=2000,a,count=0;
    scanf("%d",&n);
    if(n>=2001&&n<=2100){
    while(i<=n){
        if(i%4==0&&i%100!=0){
            a=i;
            printf("%d\n",a);
            count++;
        }
    i++;
    }
    
    if(count==0)
        printf("None");
}
    else
    printf("Invalid year!");
    return 0;
} 

解题思路：

1.定义整型变量i=2000,count=0，其余变量在后续程序运行中会被重新赋值，可以不定义；

2.用scanf函数获取用户输入，将其值赋值给n；

3.用if——else语句，区分用户输入的年份是否为21世纪有效年份，如果是有效年份进入while循环，如果不是，进入eles语句输出非法年份（Invalid year）;

4.进入while要判断从i到n中所有年份是否为闰年，故条件语句为i<=n;而判断闰年的语句为(i%4==0&&i%100!=0)，将if语句嵌套在while语句内，如果满足闰年条件则count加上1，输出i的值，如果判断为否，就什么也不做。待到判断结束后执行i++，跳入下一循环

5.判断count是否为0，满足条件输出None

流程图：

 

pta运行结果：

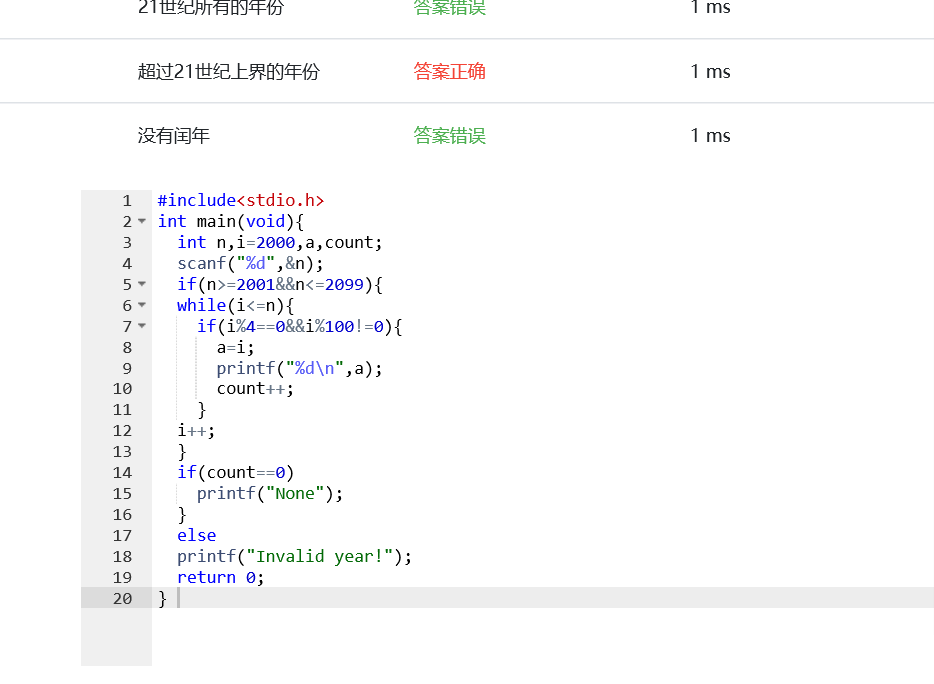
“没有闰年”部分出了错；而这部分的语句是if(count==0)
        printf("None");
于是我判断是count出了错，而之前的语句count只有加，如果一次都不进行，就是count的初始值出现了错误。我开始用DveC++尝试调试，再添加count的变量查看后，果然出现了意想中的错误

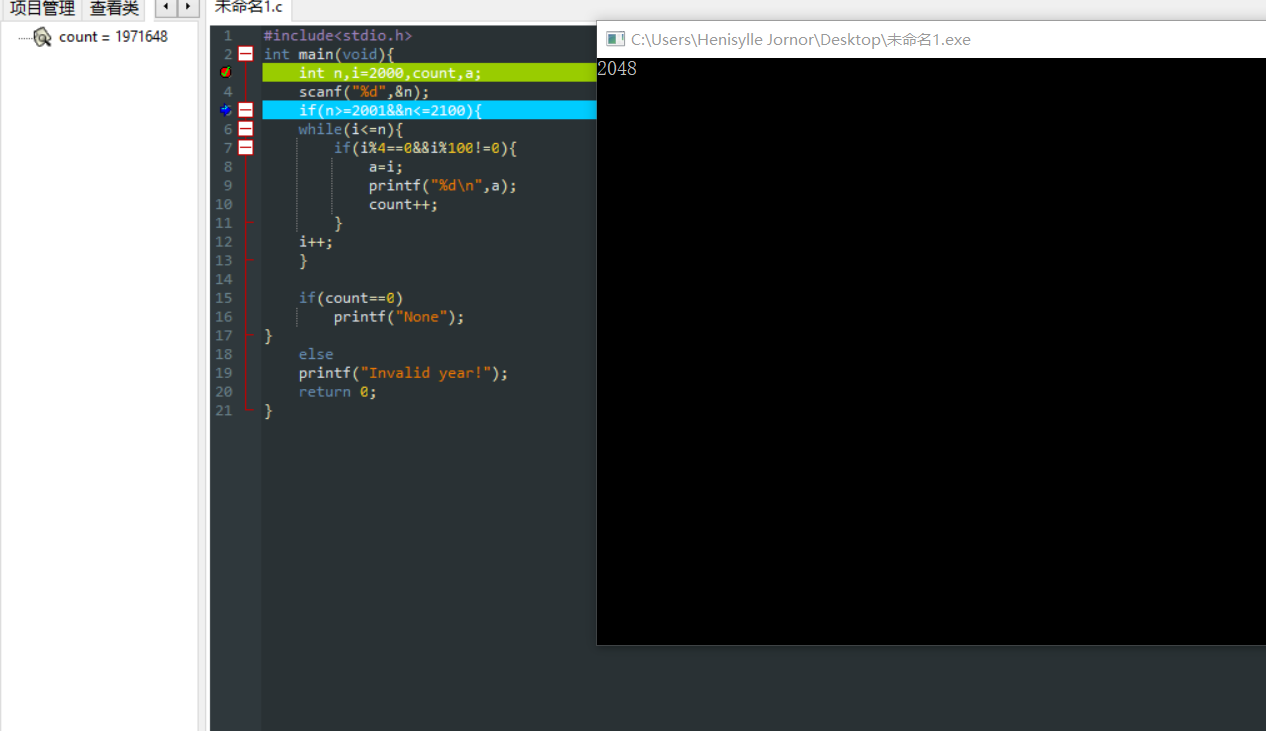
count的值为1971648，把count的初始值设为0后，这个测试点就过了，我在查询了21世纪年份得知是2001年到2099年后，修改了第一个if判断里面的数据，于是这题就解决了。

然后用正确的变量调试：

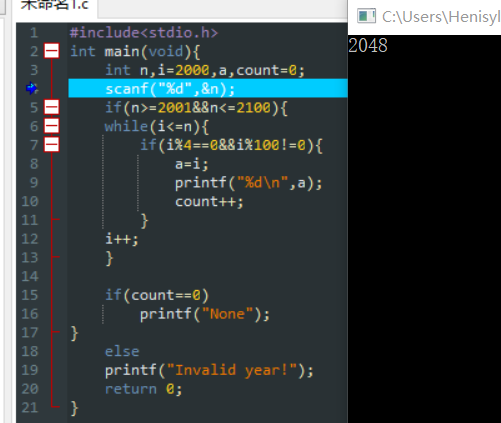
由于i的初始值被设置为2000；不满足if条件直接跳到i++；

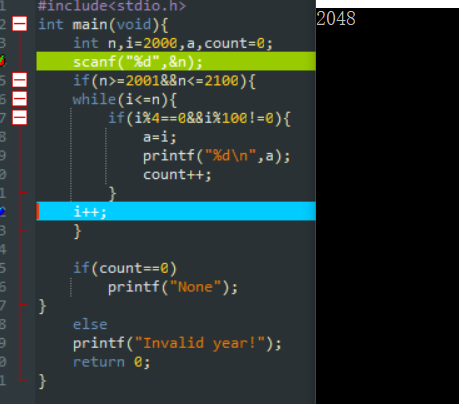
以后每满足闰年条件一次count变量的值就加1，执行界面就输出一个闰年年份，直到2048为止。

 

 

 

 

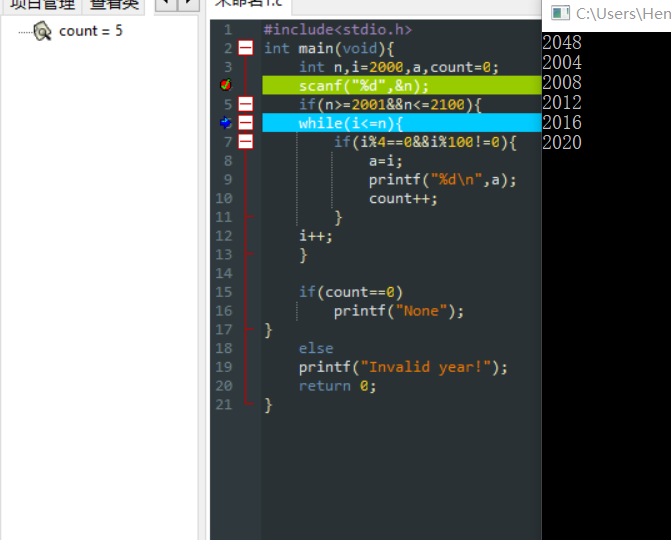
第13周第10次作业：最大公约数和最小公倍数

 

#include<stdio.h>
int main(void)
{
 int M,N,number,residue,i,t,n,x=0;
 scanf("%d %d",&M,&N);
 if(M>1000||N>1000){
  return 0;
 }
 i=M;t=N;
 do{
  number=M/N;
  residual=M-number*N;
  M=N;
  N=residual;
 }while(residual!=0);
 i=i/M;t=t/M;
 for(x=1;x<i*t;x++)
 {
  if(x%i==0&&x%t==0)
  break;
 }
 x=x*M;
 printf("%d %d",M,x);
 return 0;
 }

解题思路：

1.定义整型变量M,N,number,residue,i,t,n,x=0;

2.获取用户输入，进入if语句判断M,N是否有一个>1000

3.利用i,t分别储存M,N的用户初始输入值；

4.进入do——while语句，利用欧几里得算法，求解余数，每次运算一次把N的值赋给M，而N的值为余数的值即residue

5.循环进行，直到余数为0跳出程序，此时M的值为最大公约数，再进行i=i/M;t=t/M运算，求赋值后i，n的最大公倍数，乘以最大公约数即为最大公倍数。

流程图：

欧几里得算法范例：

 

 

dev C++调试结果，为便于观察变量变化，添加了变量查看：

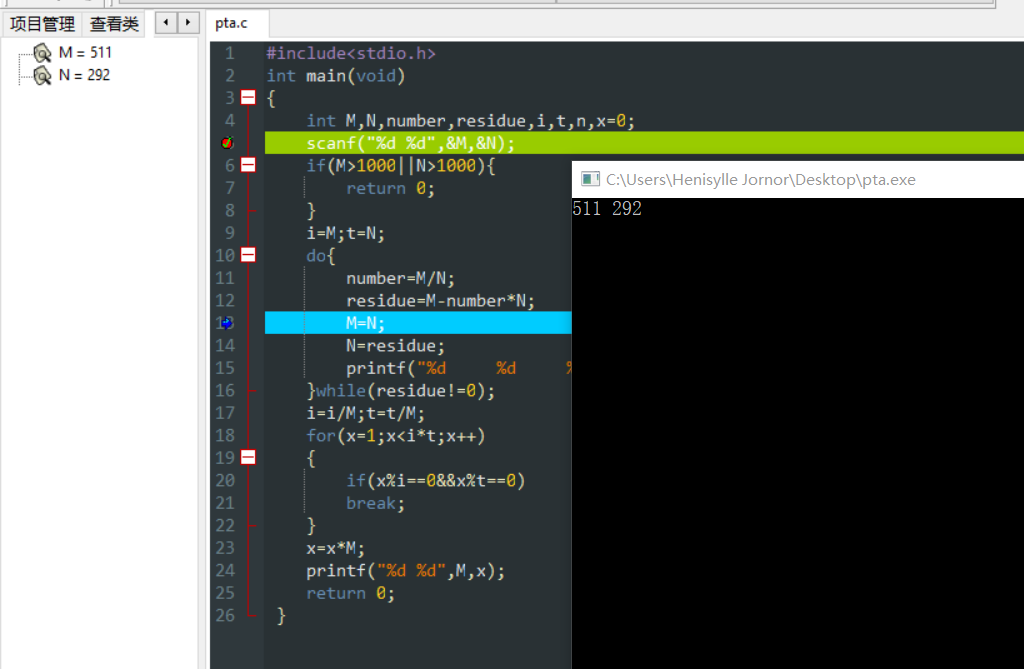
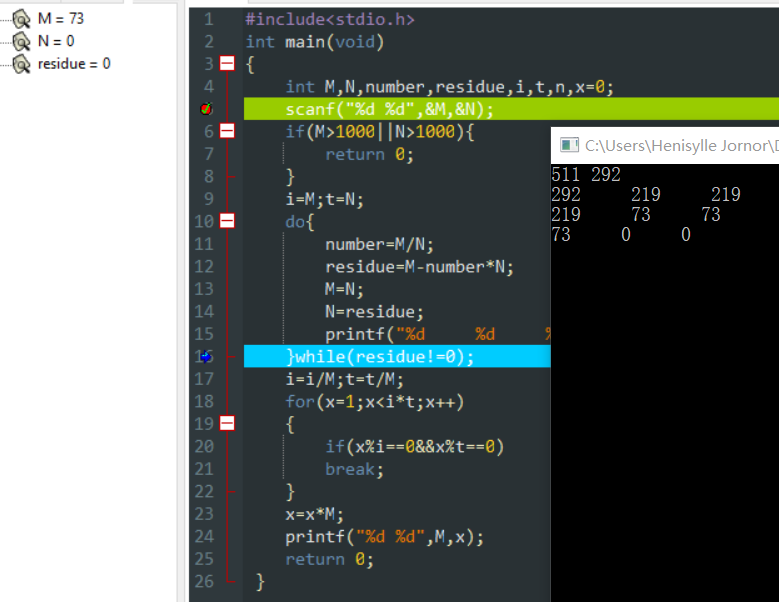
从运算过程看出欧几里得算法仅仅经过三次运算就得到了正确的最大公约数，大大减少了计算机的运算量

 

 个人总结：

这几周主要学习了循环嵌套，通过上课理解了for循环while和do-while循环的差别，通过自主学习明白了可以在语句中添加printf函数查看变量的变化，来找出程序的错误。课本上的猜数程序源代码还出现了一些现在不常用的语句如srand（time（0）），目前还没有掌握。通过各种函数的组合实现各种各样的运算让我领略了代码的简洁高效

难点：在嵌套循环的某些运算中，要求变量初始值在循环完成后仍不变，那么在什么地方定义变量的初始值就是一个难点，有些变量的定义数值直接放在数值型引入变量后，有些则放在外层循环前，有些则放在嵌套内循环前、外层循环内，这需要我们加深对运算过程的理解才能少犯类似的错误

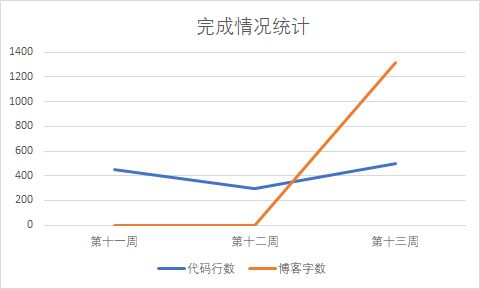
三周代码行数/博客字数统计：

 

 

                                                          

 

 所评论博客：https://www.cnblogs.com/chumengGTRlhz/p/9991154.html

                      https://www.cnblogs.com/freedomjdp/p/9979139.html

                      https://www.cnblogs.com/abcdsjjs/p/10029383.html