51Nod 1119 - 机器人走方格 V2(组合数+逆元)
题目链接 https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1119
M * N的方格,一个机器人从左上走到右下,只能向右或向下走。有多少种不同的走法?由于方法数量可能很大,只需要输出Mod 10^9 + 7的结果。
Input
第1行,2个数M,N,中间用空格隔开。(2 <= m,n <= 1000000)
Output
输出走法的数量 Mod 10^9 + 7。
Sample Input
2 3
Sample Output
3
【思路】
很容易想到用dp做,设dp(i,j)表示走到第i行,第j列的方法数,那么dp(i,j)=dp(i-1,j)+dp(i,j-1),按照这个公式递推求解即可,但是这道题的数据范围很大,n,m都是1e6的级别,这样递推肯定超时。细心观察一下这个递推方程,其实和组合数C的递推式子是很相似的,C(N,M)=C(N-1,M)+C(N-1,M-1),所以我们可以先按照原来的思路打表看一看结果有什么规律
打表的程序
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int maxn=1005;
int m,n;
int dp[maxn][maxn];
int main(){
for(int j=1;j<=10;++j) dp[1][j]=1;
for(int i=2;i<=10;++i){
for(int j=1;j<=10;++j){
dp[i][j]=dp[i-1][j];
if(j>=2) dp[i][j]+=dp[i][j-1];
}
}
for(int i=1;i<=10;++i){
for(int j=1;j<=10;++j){
cout<<setw(6)<<dp[i][j];
}
cout<<endl;
}
return 0;
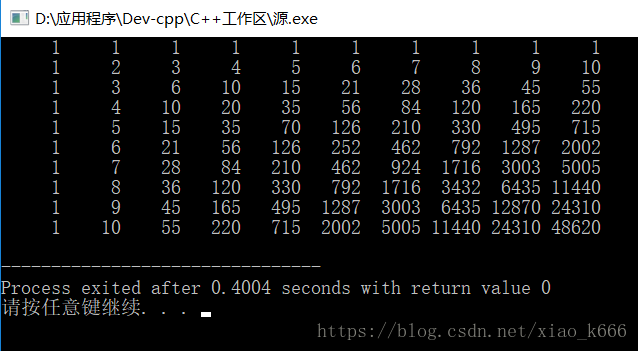
} 可以看到规律了,从左下往右上看,其实就是“斜着的”组合数,稍微归纳以下即可得出答案就是C(n+m-2,min(n,m)-1),用组合数的定义C(N,M)=N!/(M!(N-M)!)即可求解,注意要用到乘法逆元,用欧几里德或者快速幂都行。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
void gcd(ll a,ll b,ll &d,ll& x,ll& y){
if (0==b) { d=a;x=1;y=0; }
else { gcd(b,a%b,d,y,x);y-=x*(a / b); }
}
ll inv(ll a,ll p){
ll d,x,y;
gcd(a,p,d,x,y);
return d==1?(x+p)%p:-1;
}
ll m,n;
int main(){
scanf("%lld%lld",&m,&n);
if(m<n) swap(m,n);
ll ans=1,fac=1;
for(ll i=1;i<=n-1;++i) fac=(fac*i)%mod;
for(ll i=m;i<=m+n-2;++i) ans=(ans*i)%mod;
ans=ans*inv(fac,mod)%mod;
printf("%lld\n",ans);
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号