51Nod 1204 - Parity（并查集）

【题目描述】

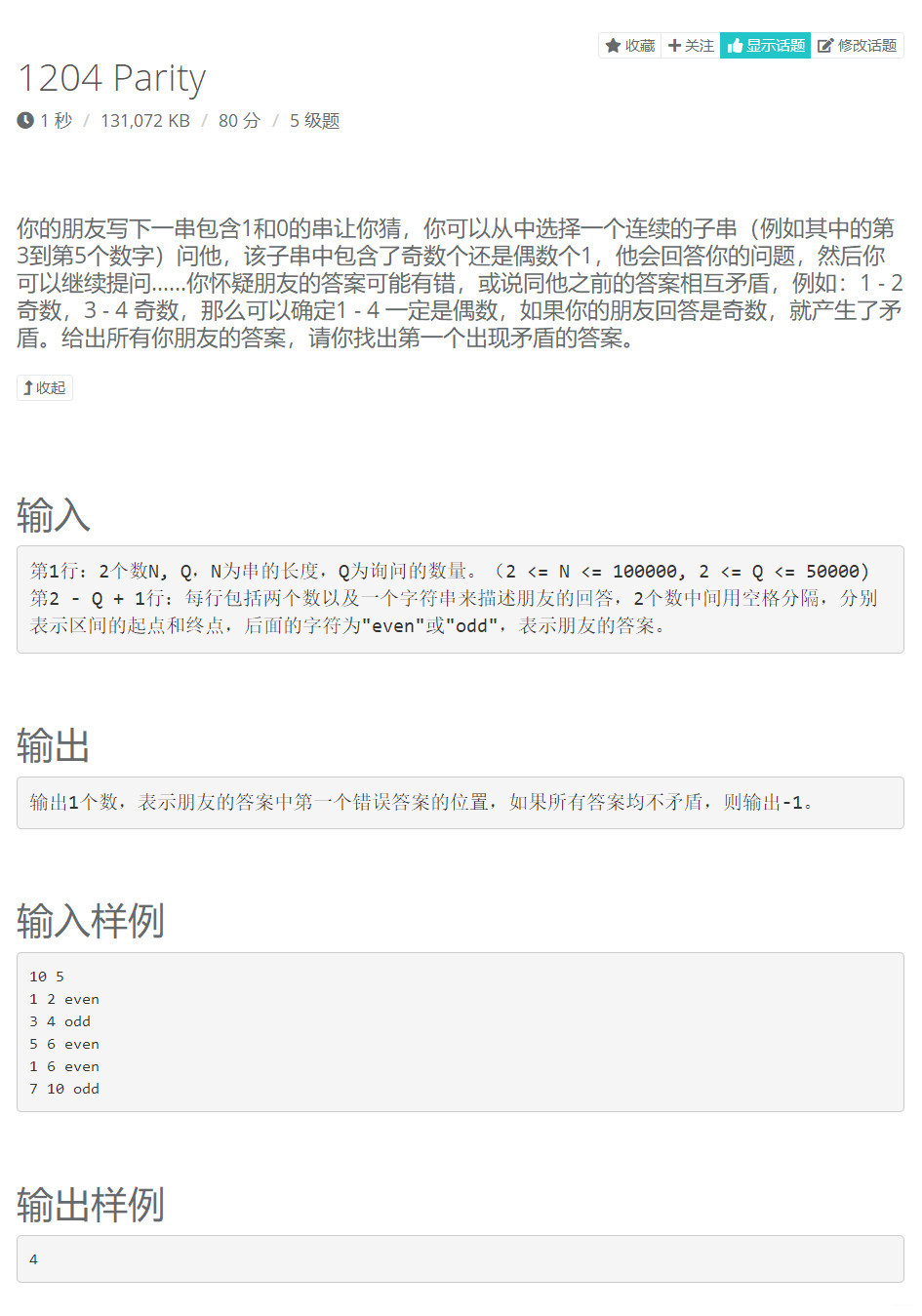
【思路】
并查集
这题要转化一下，一转化就比较明显了。我们定义前缀和为 $sum[i]$ 表示 $1$ 到 $i$ 的和，那么 $sum[b]-sum[a-1]=c[a]+c[a+1]+c[a+2]……c[b]$， 即序列的 $[a,b]$ 区间和
因为序列中只有 $0,1$ 所以区间和的奇偶性就是该区间拥有 $1$ 的奇偶数，即 $[a,b]$ 有偶数个 $1$ 的话 $[a,b]$ 区间和为偶数，同时也可知 $sum[b]$ 和 $sum[a-1]$ 同偶或同奇，即奇偶性相同如果 $[a,b]$ 中有奇数个 $1$ ，那么 $sum[b]$ 和 $sum[a-1]$ 奇偶性不同
所以这个转化关系就出来了：$[a,b]$ 有偶数个 $1$，那么 $sum[a-1]$ 和 $sum[b]$ 的奇偶性相同 ； $[a,b]$ 有奇数个 $1$ ，那么 $sum[a-1]$ 和 $sum[b]$ 的奇偶性不同,而无论如何都好，$sum[i]$ 的奇偶性只能是两种，或奇或偶，所以其实 $sum[0],sum[1],sum[2],……sum[n]$ 其实分成了两个阵营，也就是两个集合
如果读入了 $[a,b]$ 为偶数，$sum[a-1]$ 和 $sum[b]$，应该在同一个集合中。如果它们互相在对方的敌对集合中，那么矛盾，跳出，否则的话，记得合并
它们为 $1$ 个集合，并且他们的敌对集合也要合并为 $1$ 个集合
如果读入 $[a,b]$ 为奇数，$sum[a-1]$ 和 $sum[b]$，应该不在同一个集合中并且应该在对方的敌对集合中。如果它们在同一个集合中，那么矛盾，跳出，
否则的话，$sum[a-1]$ 合并到 $sum[b]$ 的敌对集合中，$sum[b]$ 合并到 $sum[i-1]$ 的敌对集合中

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int maxn=100005;

int n,q;
int a[maxn],b[maxn];
char s[maxn][15];
int par[maxn<<1];

int findst(int x){
	if(x==par[x]) return x;
	return par[x]=findst(par[x]);
}

int main(){
	scanf("%d%d",&n,&q);
	for(int i=0;i<=(n+1)*2;++i) par[i]=i;
	for(int i=1;i<=q;++i) scanf("%d%d%s",&a[i],&b[i],s[i]);
	bool flag=false;
	for(int i=1;i<=q;++i){
		int ra1=findst(a[i]-1),ra2=findst(a[i]-1+(n+1));
		int rb1=findst(b[i]),  rb2=findst(b[i]+(n+1));
		if(!strcmp(s[i],"odd")){
			if(ra1==rb1 && ra2==rb2){
				flag=true;
				printf("%d\n",i);
				break;
			}
			par[ra1]=rb2;
			par[ra2]=rb1;
		}
		else{
			if(ra1==rb2 && ra2==rb1){
				flag=true;
				printf("%d\n",i);
				break;
			}
			par[ra1]=rb1;
			par[ra2]=rb2;
		}
	}
	if(!flag) puts("-1");
	return 0;
}