51Nod 1217 - Minimum Modular(数论)
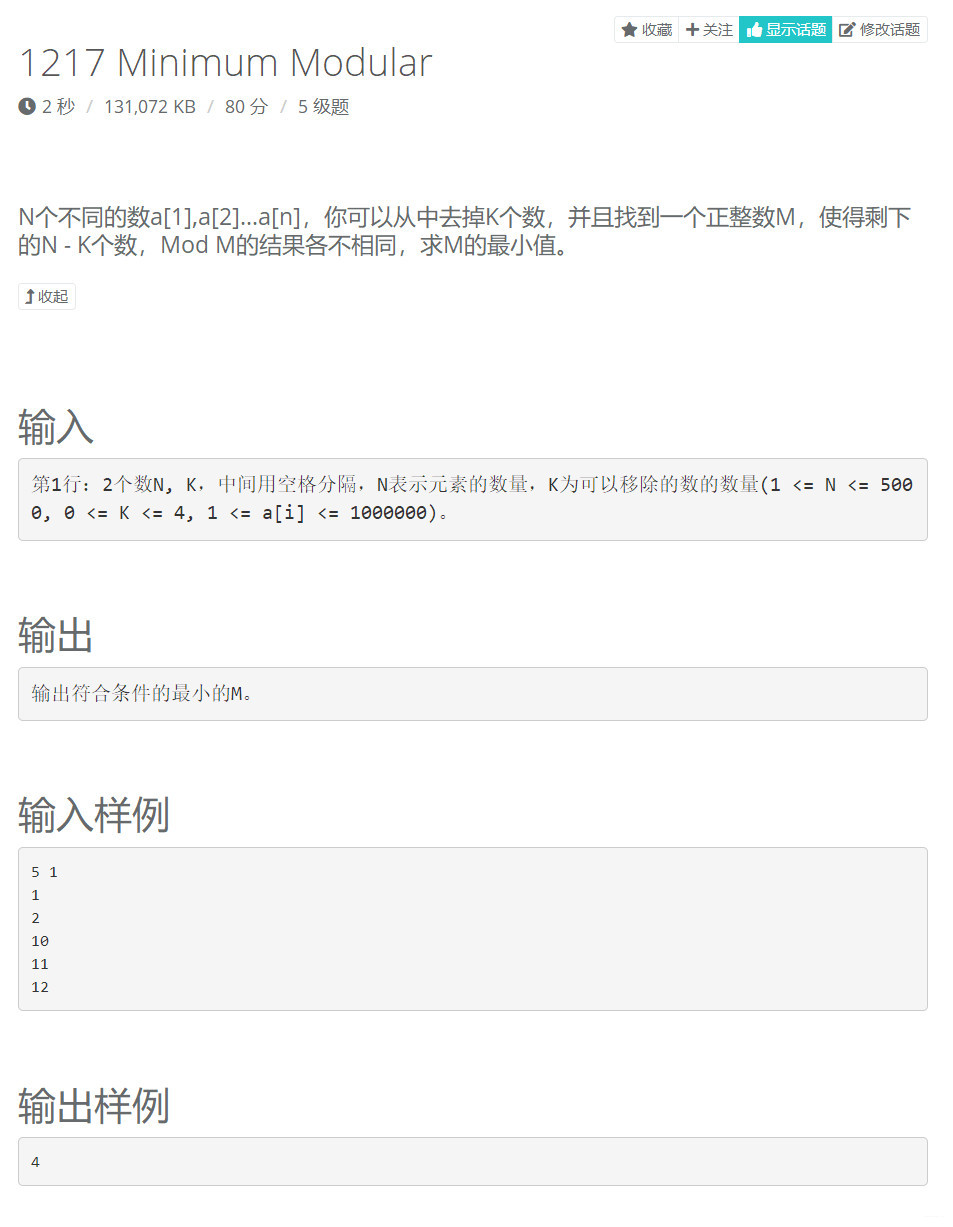
【题目描述】
【思路】
这个题我们可以考虑从小到大枚举m(从max(1,n-k)到max(a[i])+1),然后判断能否在删不超过k个数的情况下满足每个数模m都互不相同。
对于模m的情况,a[i]≡a[j](mod m)当且仅当a[i]-a[j]是m的倍数,我们可以先预处理出a[i]-a[j]=w的个数cnt[w],然后对于模m的情况,就只用考虑删m|a[i]-a[j]的i或j了,根据调和级数我们可以算出枚举1p里每个数在1p里的倍数的时间复杂度是O(plogp)的,对于此题,p<=10^6+1,可以承受。
而k个模m同余的数最多可可以形成k*(k+1)/2对同余二元组(i,j),所以对于每个m,我们可以算出满足m|w的cnt[w]之和,如果超过k*(k+1)/2就可以直接确定这个m不可行。否则就暴力计算模m是否可行。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxa=1000005;
const int maxn=5005;
int n,k;
int a[maxn],num[maxa];
bool used[maxa];
int main(){
scanf("%d%d",&n,&k);
for(int i=0;i<n;++i) scanf("%d",&a[i]);
sort(a,a+n);
for(int i=0;i<n;++i){
for(int j=i+1;j<n;++j){
++num[a[j]-a[i]];
}
}
int m=n-k;
while(1){
int cnt=0;
for(int i=m;i<maxa;i+=m) cnt+=num[i];
if(cnt>(k+1)*k/2){
++m;
continue;
}
cnt=0;
for(int i=0;i<m;++i) used[i]=false;
for(int i=0;i<n;++i){
int x=a[i]%m;
if(used[x]) ++cnt;
used[x]=true;
}
if(cnt<=k) break;
else ++m;
}
printf("%d\n",m);
return 0;
}



