51Nod 1225 - 余数之和（整除分块）

【题目描述】

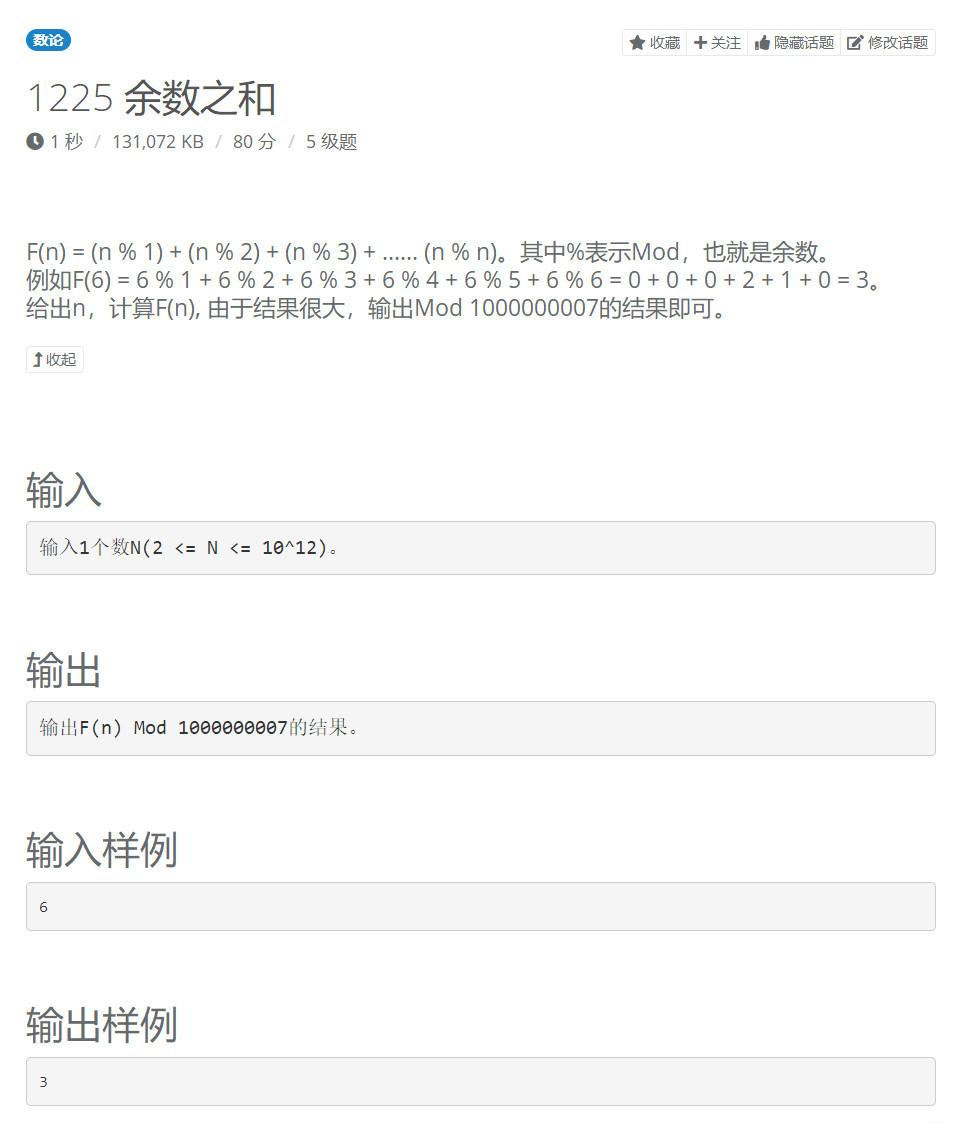
【思路】
整除分块+等差数列
设 $p =\lfloor \frac{k}{i} \rfloor , k \ mod \ i =k-pi$ 如果有$\lfloor \frac{k}{i+1} \rfloor = p, k \ mod \ (i+1) = k-p(i+1)=k-pi-p=k \ mod \ i - p$ 说明只要 $k$ 除以 $i$ 的整数部分相同，那么 $k \ mod \ i$ 就会形成一个等差数列，用一次求和公式即可

#include<bits/stdc++.h>
using namespace std;
const long long mod=1000000007;

int main(){
	long long n,ans=0,inv2=(mod+1)/2;
	scanf("%lld",&n);
	for(long long L=1,R;L<=n;L=R+1){
		R=n/(n/L);
		ans=(ans+(R-L+1)%mod*((n%L+n%R)%mod)%mod*inv2%mod)%mod;
	}
	printf("%lld\n",ans);
	return 0;
}