高斯模型
一、高斯分布
1.概念
高斯分布，也叫正态分布，是一种连续型变量的概率分布。
（1）正态分布：就是正常形态的分布，符合自然规律。例如体重、身高、收入等都符合正态分布，大部分处于中等水平，特别少和特别多的比例都比较低；
（2）连续型变量的概率分布：例如抛10次硬币，正面加一分，反面扣一分；最终结果-10分和10分的概率比较低，0分的概率比较高。可以说该事件发生的概率出现了正态分布。
2.公式
假设P(Xj=xj|Y=Ck)服从高斯分布：每个特征Xj分到每个类别Ck的条件概率
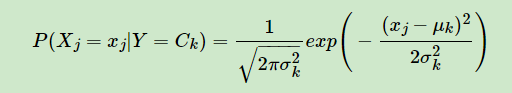
其中：
（1）Ck为Y的第k类类别
（2）μk和(σk)^2为需要从训练集估计的值
（3）exp表示e的某次方
3.例子
from sklearn import datasets # 导入sklearn模块中的数据集
iris = datasets.load_iris()#导入鸢尾花数据
from sklearn.naive_bayes import GaussianNB#导入朴素贝叶斯模块下的高斯贝叶斯函数
gnb = GaussianNB()
y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d" % (iris.data.shape[0],(iris.target != y_pred).sum()))
print(iris.data.shape)#数据集的行数、列数
print(y_pred)#fit数据拟合后，predict预测结果
print(iris.target )#存储了数据集中每条记录属于哪一鸢尾植物，target为分类标签，与data中的数据相对应
（1）在Sklearn机器学习包中，集成了各种各样的数据集，包括糖尿病数据集、手写数字数据集、乳腺癌数据集、体能训练数据集等。
这里引入的是鸢尾花卉（Iris）数据集，它是很常用的一个数据集。鸢尾花有三个亚属，分别是山鸢尾（Iris-setosa）、变色鸢尾（Iris-versicolor）和维吉尼亚鸢尾（Iris-virginica）。
该数据集一共包含4个特征变量，1个类别变量。共有150个样本，iris是鸢尾植物，这里存储了其萼片和花瓣的长宽，共4个属性，鸢尾植物分三类。如下表所示：
（2）iris里有两个属性iris.data，iris.target。
data是一个矩阵，每一列代表了萼片或花瓣的长宽，一共4列，每一列代表某个被测量的鸢尾植物，一共采样了150条记录。
target是一个数组，存储了data中每条记录属于哪一类鸢尾植物，所以数组的长度是150，数组元素的值因为共有3类鸢尾植物，所以不同值只有3个。种类为山鸢尾、杂色鸢尾、维吉尼亚鸢尾。target为分类标签，与data中的数据相对应。
print(iris.data)
print(iris.target )
（3）在使用GaussianNB的fit方法拟合数据后，我们可以进行预测。此时预测有三种方法，包括predict，predict_log_proba和predict_proba。
predict是训练后返回预测结果，是标签值:预测每条记录属于哪一类别的结果，例如上表中鸢尾花标签class值。
print(gnb.fit(iris.data, iris.target).predict(iris.data))
predict_proba则不同，它会给出测试集样本在各个类别上预测的概率。返回的是一个 n 行 k 列的数组， 第 i 行 第 j 列上的数值是模型预测 第 i 个预测样本为某个标签的概率，并且每一行的概率和为1。
print(gnb.fit(iris.data, iris.target).predict_proba(iris.data))
predict_log_proba和predict_proba类似，它会给出测试集样本在各个类别上预测的概率的一个对数转化。
print(gnb.fit(iris.data, iris.target).predict_log_proba(iris.data))
