贝叶斯算法
一、贝叶斯公式
贝叶斯公式基于条件独立,通过条件概率公式和全概率公式推导而来。
1.条件独立
条件独立的公式如下,其含义是当C发生时,A、B的发生互不干扰。
P(A∩B|C)=P(A|C)∩P(B|C)<=>P(A|B,C)=P(A|C)<=>A,B对于C是条件独立的
2.条件概率公式
P(A|B)=P(AB)/P(B)
变形公式:P(AB)=P(A|B)·P(B)=P(B|A)·P(A)
3.全概率公式
如果事件B1、B2、B3…Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有
P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn)。
或者:p(A)=P(AB1)+P(AB2)+...+P(ABn)(其中A与Bn的关系为交)
4.贝叶斯公式
贝叶斯定义用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。下面是贝叶斯公式推导过程,其中①②③都是贝叶斯公式的变形。
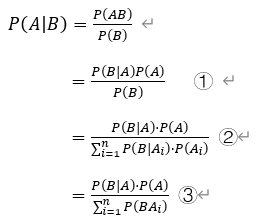
二、朴素贝叶斯分类
1.概念
贝叶斯分类是一类以贝叶斯定理为基础的分类算法的总称,朴素贝叶斯分类是其中之一,这里的“朴素”指各个特征之间是相互独立、互不影响的。主要应用于:求已知一些特征函数,求其属于某一类别的概率。
P(类别|特征1,特征2,特征3...)=P(特征1,特征2,特征3...|类别)·P(类别)/P(特征1,特征2,特征3...)
假设各个特征相互独立,则:
P(类别|特征1,特征2,特征3...)=P(特征1,特征2,特征3...|类别)·P(类别)/[P(特征1)·P(特征2)·P(特征3)·...]
2.实例
我们想知道考试前一天逛街、刷视频、玩游戏、学习对成绩的影响。设:成绩优秀为1,成绩差为0;考试前一天逛街了为1,没有为0;考试前一天刷视频了为1,没有为0;考试前一天玩游戏了为1,没有为0;考试前一天学习了为1,没有为0。现有如下样本库:
| 成绩 | 逛街 | 刷视频 | 玩游戏 | |
| ① | 0 | 1 | 1 | 1 |
| ② | 0 | 1 | 0 | 1 |
| ③ | 1 | 0 | 0 | 0 |
| ④ | 0 | 0 | 0 | 0 |
| ⑤ | 1 | 0 | 0 | 1 |
| ⑥ | 0 | 0 | 1 | 1 |
| ⑦ | 0 | 1 | 0 | 0 |
| ⑧ | 1 | 1 | 0 | 1 |
| ⑨ | 0 | 1 | 0 | 1 |
| ⑩ | 0 | 1 | 0 | 1 |
求考试前一天逛街了,玩游戏了,没有刷视频、学习,成绩优秀的概率是多少?
P(1|1,0,1,0)
=P(1,1,0,1,0)/[P(逛街=1)·P(刷视频=0)·P(玩游戏=1)·P(学习=0)]
=0.1/(0.6 * 0.8 * 0.7 * 0.7)
=0.4252
我们再来算一下成绩差的概率为多少
P(0|1,0,1,0)
=P(0,1,0,1,0)/[P(逛街=1)·P(刷视频=0)·P(玩游戏=1)·P(学习=0)]
=0.2/(0.6 * 0.8 * 0.7 * 0.7)
=0.8503
通过上面的计算,我们发现两个概率之和并不等于1。实际上在朴素贝叶斯分类器中,通过比较两个概率大小,判断属于哪个类别。由于分母时一样的,我们通常省去分母,只比较分子。
三、拉普拉斯平滑
拉普拉斯平滑主要处理零概率问题,就是在计算实例的概率时,如果某个量x,在观察样本库(训练集)中没有出现过,会导致整个实例的概率结果是0。在文本分类的问题中,当一个词语没有在训练样本中出现,该词语调概率为0,使用连乘计算文本出现概率时也为0。这是不合理的,不能因为一个事件没有观察到就武断的认为该事件的概率是0。
为了解决零概率的问题,法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加法平滑也叫做拉普拉斯平滑。假定训练样本很大时,每个分量x的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。
四、项目实战
1.
(1)
朴素贝叶斯根据先验概率(特征的可能性分布)有三种模型:高斯贝叶斯、伯努利贝叶斯、多项式贝叶斯。这三个类适用的分类场景各不相同,一般来说,如果样本特征的分布大部分是连续值,使用GaussianNB会比较好。如果样本特征的分布大部分是多元离散值,使用MultinomialNB比较合适。而如果样本特征是二元离散值或者很稀疏的多元离散值,应该使用BernoulliNB。
sklearn 库中的 naive_bayes 模块实现了 5 种朴素贝叶斯算法:高斯贝叶斯、伯努利贝叶斯、多项式贝叶斯、分类贝叶斯、补充贝叶斯。
后缀NB是朴素贝叶斯(Naive Bayes)的缩写
Accuray表示测试集的准确率,cv=10表示十折交叉验证
下面代码举了三种朴素贝叶斯分类,如果想看高斯朴素贝叶斯,把前三行代码高斯朴素贝叶斯取消注释,另两个注释,并将qnb=MultinomialNB()改为qnb=GaussianNB()。
#from sklearn.naive_bayes import GaussianNB#高斯分布下的朴素贝叶斯分类
#from sklearn.naive_bayes import BernoulliNB#驳伯努利分布
from sklearn.naive_bayes import MultinomialNB#多项分布
from sklearn.model_selection import cross_val_score
from sklearn import datasets
iris=datasets.load_iris()
print(iris)
qnb=MultinomialNB()
scores=cross_val_score(qnb,iris.data,iris.target,cv=10,scoring='accuracy')
print('Accuracy:%.3f'%scores.mean())
若没有安装sklearn包,在终端输入pip install sklearn即可。
cd C:\Users\WAFF\AppData\Local\Programs\Python\Python37\Scripts
pip install sklearn
(2)k折交叉验证
数据集包括训练集和测试集,我们一般用准确率Auc,即分类正确的样本个数占总样本的比例,来评价分类器的好坏。
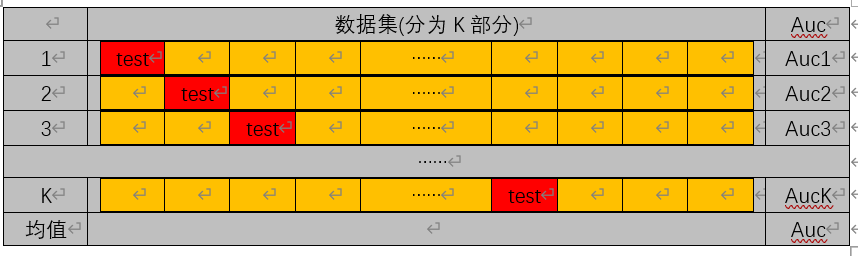
k折交叉验证,指将数据集分K个部分(K个格子):红色为测试集test,橙色为训练集train,每次划分都有一个准确率Auci,取其平均值为最终的准率率。
2.垃圾邮件分类器
垃圾邮件分类器,功能是将邮件样本集中垃圾邮件分类出来。以英文邮件为例,主要步骤为:
(1)查看数据data:邮件内容
(2)分词:句子->单词,以空格为标识
(3)向量化:单词->数字->二进制
(4)朴素贝叶斯公式:P(类别|单词1,单词2,单词3,...)=P(单词i|类别)*P(类别)/P(单词i)
(5)结果
代码中解释非常详细
#朴素贝叶斯分类器训练函数
#
def trainNB0(trainMatrix,trainCategory):
#总文件数
numTrainDocs=len(trainMatrix)
#总单词数
numWords=len(trainMatrix[0])
#侮辱性文件出现概率
pAbusive=sum(trainCategory)/float(numTrainDocs)
#构造单词出现次数列表
#p0Num正确的统计
#p1Num侮辱的统计
p0Num=np.ones(numWords)
p1Num=np.ones(numWords)
#整个数据集单词出现的总数,根据样本/实际调查结果调整分母的值
global p0Denom
global p1Denom
p0Denom=2.0
p1Denom=2.0
for i in range(numTrainDocs):
if trainCategory[i]==1:
#累加辱骂词的频次
p1Num+=trainMatrix[i]
#对每篇文章的辱骂的频次 进行统计汇总
p1Denom+=sum(trainMatrix[i])
else:
p0Num+=trainMatrix[i]
p0Denom+=sum(trainMatrix[i])
#类别1 即侮辱性文档的[log(F1/C1),log(F2/C2),log(F3/C3)...]避免0的产生,拉普拉斯平滑的一种方法取log?
p1Vect=np.log(p1Num/p1Denom)
#类别0 即正常文档的[log(F0/C0),log(F0/C0),log(F0/C0)...]
p0Vect=np.log(p0Num/p0Denom)
return p0Vect,p1Vect,pAbusive
#切分文本
def textParse(bigString):
'''
Desc:
接收一个大字符串并将其解析为字符串列表
Args:
bigString--大字符串
jieba 中文切分,自己查
Returns:
去掉少于2个字符的字符串,并将所有字符串转换为小写,返回字符串列表
'''
import re
#使用正则表达式来切分句子,其中分隔符是除单词、数字外的任意字符串
list0fTokens=re.split(r'\w*',bigString)
return [tok.lower() for tok in list0fTokens if len(tok)>2]
def createVocabList1(dataSet):
'''
获取所有单词的集合
:param dataSet:数据集
:return:所有单词的集合(即不含重复元素的列表)
'''
vocabSet=set([])#creat empty set
for document in dataSet:
#操作符|用于求两个集合的并集
vocabSet=vocabSet|set(document)#union of the two sets
return list(vocabSet)
def set0fWords2Vec(vocabList1,inputSet):
'''
遍历查看该单词是否出现,出现该单词则将该单词置1
:param vocabList1:所有单词集合列表
:return:匹配列表[0,1,0,1...],其中1与0表示词汇表中的单词是否出现在输入的数据集中
'''
#创建一个和词汇表等长的向量,并将其元素都设置为0
returnVec=[0]*len(vocabList1)#[0,0,0...]
#遍历文档中所有单词,如果出现了词汇表中的单词,则输出的文档向量中的对应值设为1
for word in inputSet:
if word in vocabList1:
returnVec[vocabList1.index(word)]=1
else:
print ("the word :%s is not in my Vocabulary!" %word)
return returnVec
#朴素贝叶斯分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
p1=sum(vec2Classify*p1Vec)+np.log(pClass1)
p0=sum(vec2Classify*p0Vec)+np.log(1.0-pClass1)
if p1>p0:
return 1
else :
return 0
def spamTest():
'''
Desc:对贝叶斯垃圾邮件分类器进行自动化处理
Args:none
Returns:
'''
docList1=[]
classList1=[]
fullText=[]
for i in range(1,26):#前26个文件
#切分,解析数据,并归类为1类别pythonLX\0
wordList1=textParse(open('F:/Study/jupyterLX/pythonLX/0/%d.txt' % i,'r',encoding='ISO-8859-1').read())
docList1.append(wordList1)
fullText.extend(wordList1)
classList1.append(1)
#切分,解析数据,并归类为0类别
wordList1=textParse(open('F:/Study/jupyterLX/pythonLX/1/%d.txt' % i,'r',encoding='ISO-8859-1').read())
docList1.append(wordList1)
fullText.extend(wordList1)
classList1.append(0)
#创建词汇表
vocabList1=createVocabList1(docList1)
trainingSet=list(range(50))
testSet=[]
#随机取10个邮件用来测试
for i in range(10):
#random.uniform(x,y)随机生成一个范围为x-y的实数
randIndex=int(random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat=[]
trainClasses=[]
for docIndex in trainingSet:
trainMat.append(set0fWords2Vec(vocabList1,docList1[docIndex]))
trainClasses.append(classList1[docIndex])
p0v,p1v,pSpam=trainNB0(np.array(trainMat),np.array(trainClasses))
errorCount=0
for docIndex in testSet:
wordVector=set0fWords2Vec(vocabList1,docList1[docIndex])
if classifyNB(np.array(wordVector),p0v,p1v,pSpam)!=classList1[docIndex]:
errorCount+=1
print('the errorCount is :',errorCount)
print('the testSet length is :',len(testSet))
print('the error rate is :',float(errorCount)/len(testSet))
import random
import numpy as np
import math
spamTest()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号