A*寻路算法

一种用于寻找有效路径的算法。

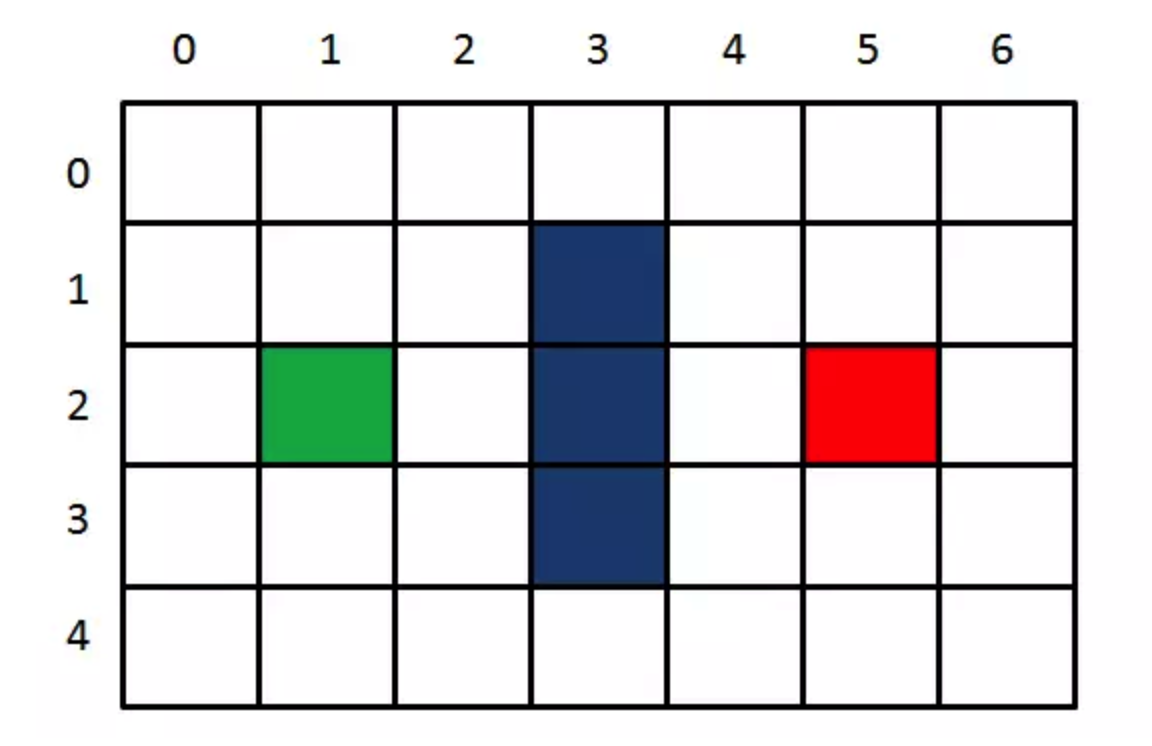
一个7×5大小的迷宫，绿色的格子是起点，红色格子是终点，中间三个蓝色格子是墙。这里对于A*寻路的描述做了很大的简化。实际场景中可能会遇到斜向移动、特殊地形等等因素，有些时候需要对OpenList中的方格进行重新标记。

游戏的规则是从起点开始，每一步只能上下左右移动一格，且不能穿越墙壁。如何让AI用最少的步数到达终点？

引入两个集合和一个公式：

OpenList：可到达的格子

CloseList：已到达的格子 

F=G+H ：对格子价值的评估，其中G代表从起点走到当前格的成本，也就是走了多少步，H代表从当前格走到目标格的距离(不考虑障碍)。F值越小越好。

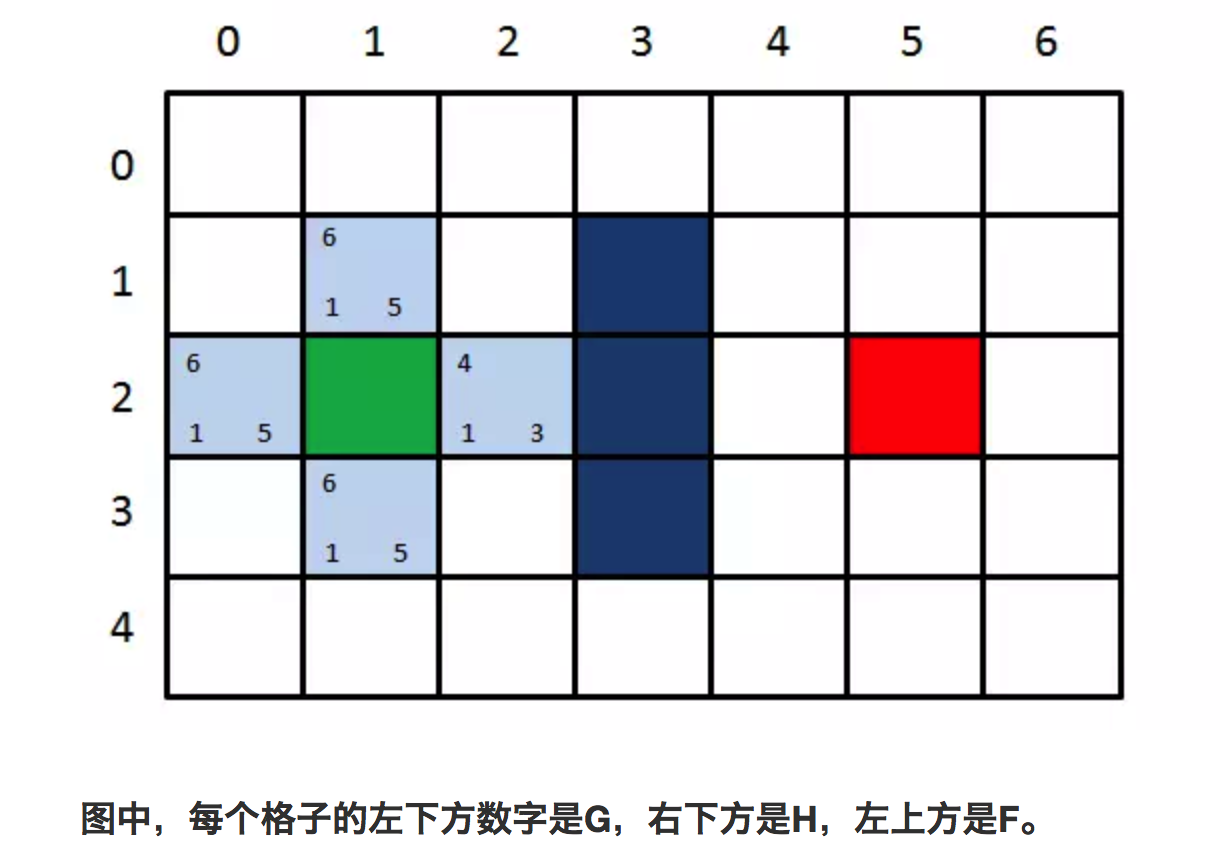
第一步：把起点放入OpenList    

OpenList：Node(1,2)

第二步：找出OpenList中F值最小的方格，即唯一的方格Node(1,2)作为当前方格，并把当前格移出OpenList，放入CloseList。代表这个格子已到达并检查过了。 

CloseList：Node(1,2)

第三步：找出当前格上下左右所有可到达的格子，看它们是否在OpenList当中。如果不在，加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父亲节点”(为了确定最终路线)。 

OpenList：Node(1,1) Node(0,2) Node(2,2) Node(1,3)

CloseList：Node(1,2) 

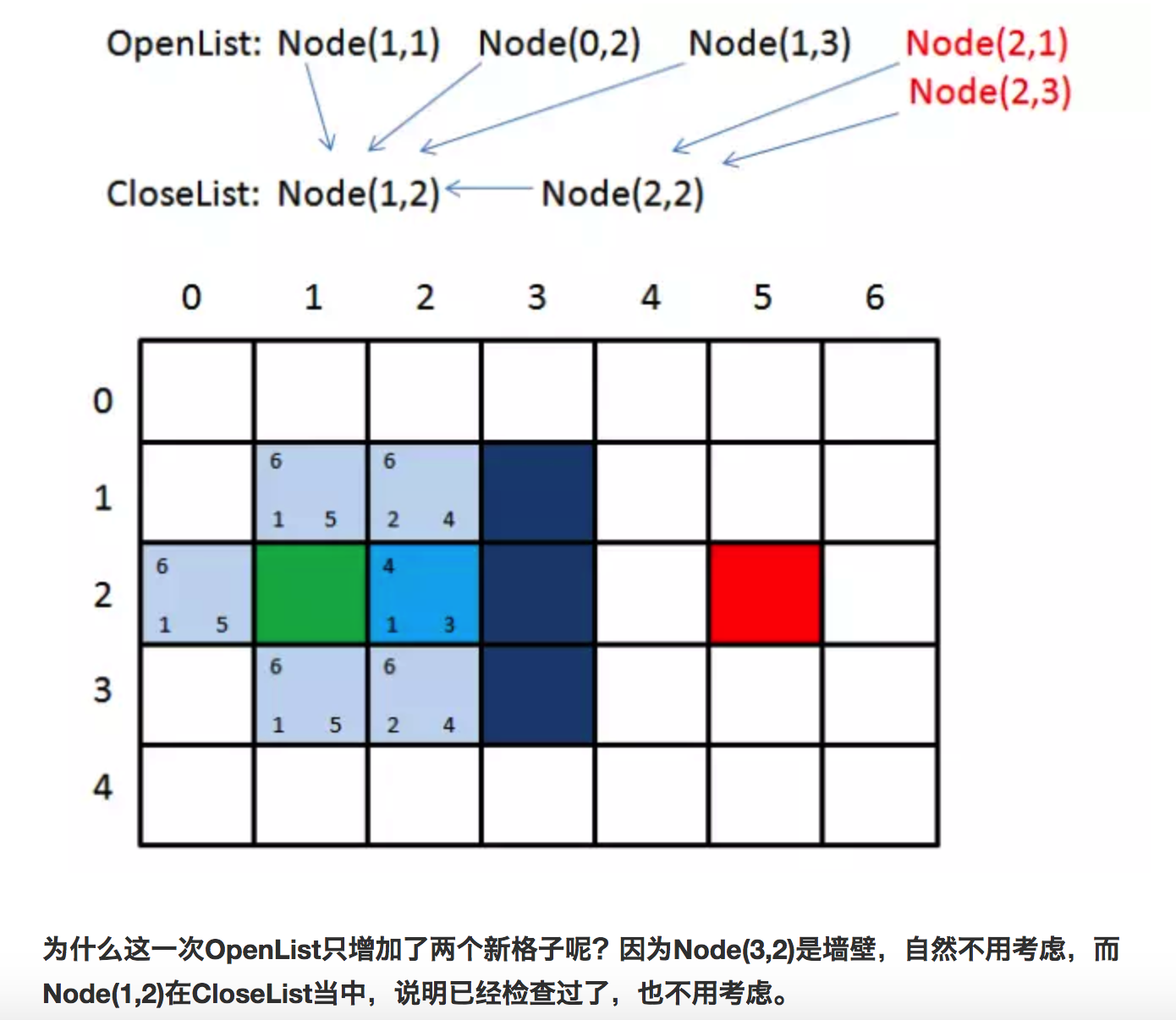
Round1 ~ 第一步：找出OpenList中F值最小的方格，即方格Node(2,2)作为当前方格，并把当前格移出OpenList，放入CloseList。代表这个格子已到达并检查过了。

OpenList：Node(1,1) Node(0,2)  Node(1,3)

CloseList：Node(1,2) Node(2,2)

Round2 ~ 第二步：找出当前格上下左右所有可到达的格子，看它们是否在OpenList当中。如果不在，加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父亲节点”。 

 

public Node aStarSearch(Node start, Node end) {
    // 把起点加入 open list  
    openList.add(start);
    //主循环，每一轮检查一个当前方格节点
    while (openList.size() > 0) {
        // 在OpenList中查找 F值最小的节点作为当前方格节点
        Node current = findMinNode();
        // 当前方格节点从open list中移除
        openList.remove(current);
        // 当前方格节点进入 close list
        closeList.add(current);
        // 找到所有邻近节点
        List<Node> neighbors = findNeighbors(current);
        for (Node node : neighbors) {
            if (!openList.contains(node)) {
                //邻近节点不在OpenList中，标记父亲、G、H、F，并放入OpenList
                markAndInvolve(current, end, node);
            }
        }
        //如果终点在OpenList中，直接返回终点格子
        if (find(openList, end) != null) {
            return find(openList, end);
        }
    }
    //OpenList用尽，仍然找不到终点，说明终点不可到达，返回空
    return null;
}