InnoDB索引概述,二分查找法,平衡二叉树

索引是应用程序设计和开发的一个重要方面。如果索引太多，应用的性能可能会受到影响；如果索引太少，对查询性能又会产生影响。要找到一个合适的平衡点，这对应用的性能至关重要。

如果知道数据的使用，从一开始就应该在需要处添加索引。开发人员对于数据库的工作往往停留在应用的层面，比如编写SQL语句、存储过程之类，他们甚至可能不知道索引的存在，或者认为事后让相关DBA加上即可。而DBA往往不了解业务的数据流，添加索引需要通过监控大量的SQL语句，从中找到问题。这个步骤需要的时间肯定是大于初始添加索引所需要的时间，并且可能会遗漏一部分索引。当然索引不是越多越好，某台MySQL服务器iostat显示磁盘使用率100%，经过分析后发现，是由于开发人员添加了太多的索引。在删除一些不必要的索引之后，磁盘使用率马上下降为20%，因此索引的添加也是有一定技巧的。

InnoDB存储引擎索引概述

InnoDB存储引擎支持两种常见的索引，一种是B+树索引，另一种是哈希索引。InnoDB存储引擎支持的哈希索引是自适应的，InnoDB存储引擎会根据表的使用情况自动为表生成哈希索引，不能人为干预是否在一张表中生成哈希索引。

B+树索引就是传统意义上的索引，这是目前关系型数据库系统中最常用、最有效的索引。B+树索引的构造类似于二叉树，根据键值（Key Value）快速找到数据。需要注意的是，B+树中的B不是代表二叉（binary），而是代表平衡（balance），因为B+树是从最早的平衡二叉树演化而来，但是B+树不是一个二叉树。

一个常常被DBA忽视的问题是：B+树索引并不能找到一个给定键值的具体行。B+树索引能找到的只是被查找数据行所在的页。然后数据库通过把页读入内存，再在内存中进行查找，最后得到查找的数据。

二分查找法

二分查找法（binary search）也称为折半查找法，用来查找一组有序的记录数组中的某一记录。其基本思想是：将记录按有序化（递增或递减）排列，查找过程中采用跳跃式方式查找，即先以有序数列的中点位置为比较对象，如果要找的元素值小于该中点元素，则将待查序列缩小为左半部分，否则为右半部分。通过一次比较，将查找区间缩小一半。

例如我们有5、10、19、21、31、37、42、48、50、52这10个数，现要从这10个数中查找48这条记录，其查找过程如图5-1所示。

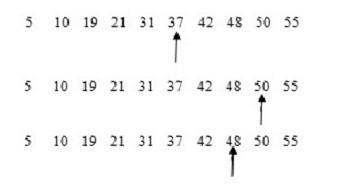
从上图可以看出，用了3次就找到了48这个数。如果是顺序查找的话，则需要8次。因此二分查找法的效率比顺序查找法要好（平均来说）。但如果查5这条记录，顺序查找只需1次，而二分查找法却需要4次。对于上面10个数来说，顺序查找的平均查找次数为（1+2+3+4+5+6+7+8+9+10）/10=5.5次，而二分查找法为（4+3+2+4+3+1+4+3+2+3）/10=2.9次。在最坏的情况下，顺序查找的次数为10，而二分查找的次数为4。

二分查找法的应用极其广泛，而且它的思想易于理解。第一个二分查找算法早在1946年就出现了，但是第一个完全正确的二分查找算法直到1962年才出现。每页Page Directory中的槽是按照主键的顺序存放的，对于某一条具体记录的查询是通过对Page Directory进行二分查找得到的。

平衡二叉树

在介绍B+树前，先要了解一下二叉查找树。B+树是通过二叉查找树，再由平衡二叉树、B树演化而来。

二叉查找树是一种经典的数据结构。下图显示了一颗二叉查找树。 

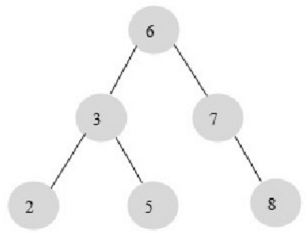
图中的数字代表每个节点的键值，二叉查找树中，左子树的键值总是小于根的键值，右子树的键值总是大于根的键值。

因此可以通过中序遍历得到键值的排序输出，中序遍历后输出：2、3、5、6、7、8。

对图的这颗二叉树进行查找，如查键值为5的记录，先找到根，其键值是6，6大于5，因此找6的左子树，找到3；而5大于3，再找右子树……一共找了3次。如果按2、3、5、6、7、8的顺序来找同样需要3次。用同样的方法再找键值为8的这个记录，这次用了3次查找，而顺序查找时需要6次。计算平均查找次数可得：顺序查找的平均查找次数为（1+2+3+4+5+6）/6=3.3次，二叉查找树的平均查找次数为（3+3+3+2+2+1）/6=2.3次。二叉查找树比顺序查找快。

二叉查找树可以任意构造，同样的2、3、5、6、7、8这五个数字，也可以按照下图所示的方式建立二叉查找树。效率较低的一颗二叉查找树。

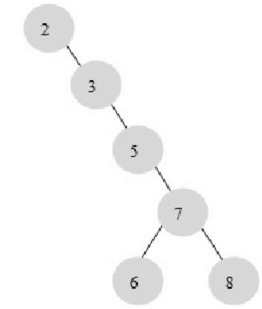
上图的平均查找次数为（1+2+3+4+5+5）/6=3.16次，和顺序查找差不多。显然这次二叉查找树的效率就低了。

因此若想最大性能地构造一个二叉查找树，需要这颗二叉查找树是平衡的，因此引出了新的定义——平衡二叉树，或称为AVL树。

平衡二叉树的定义如下：首先符合二叉查找树的定义，其次必须满足任何节点的左右两个子树的高度最大差为1。平衡二叉树对于查找的性能是比较高的，但不是最高的，只是接近最高性能。要达到最好的性能，需要建立一颗最优二叉树，但是最优二叉树的建立和维护需要大量的操作，因此我们一般只需建立一颗平衡二叉树即可。

平衡二叉树对于查询速度的确很快，但是维护一颗平衡二叉树的代价是非常大的，通常需要1次或多次左旋和右旋来得到插入或更新后树的平衡性。

当我们需要插入一个新的键值为9的节点时，需要做如下的变动。

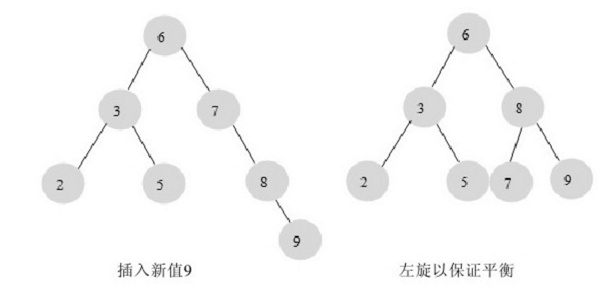
这里通过一次左旋操作就将插入后的树重新变为平衡的了。但是有的情况下可能需要多次旋转：

除了插入操作，还有更新和删除操作，不过这和插入没有本质的区别，它们都是通过左旋或者右旋来完成的。因此对于一颗平衡二叉树的维护是有一定开销的，不过平衡二叉树多用于内存结构对象中，因此维护的开销相对较小。