hdu 1005

Number Sequence

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 127502    Accepted Submission(s): 30987

Problem Description

A number sequence is defined as follows:

f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.

Given A, B, and n, you are to calculate the value of f(n).

 

 

Input

The input consists of multiple test cases. Each test case contains 3 integers A, B and n on a single line (1 <= A, B <= 1000, 1 <= n <= 100,000,000). Three zeros signal the end of input and this test case is not to be processed.

 

 

Output

For each test case, print the value of f(n) on a single line.

 

 

Sample Input

1 1 3 1 2 10 0 0 0

 

 

Sample Output

2 5

题意：给你一个方程，求f[n]，结果模7

分析：1：对7取模，f[n-1],f[n-2]，A,B固定，最多7*7=49种情况。

从3算到50，把所有的情况存起来

　　2：如果题目加难，模100000007，这种方法肯定不行，超时，当然，仅仅追求这个题目的初学者可以不用看第二份代码。

　　第二份代码思路：这是一个二维矩阵乘法，，，这就要一定功底去构造矩阵啦，然后使用快速幂取模。。。

代码一：

    //这份代码就没什么好解释了，找循环节
    #include <stdio.h>  
    int main ()  
    {      
        int f[51];  
        int a, b, n,i,T;   
        while(scanf("%d%d%d",&a,&b,&n),a||b||n)  
        {  
              f[1]=f[2]=1;  
              for (i=3;i<50;i++)  
              {  
                 f[i]=(a*f[i-1]+b*f[i-2])%7;  
                  if (f[i]==1&&f[i-1]==1)    
                  {  
                      break;  
                  }  
              }            
              T=i-2;  
              f[0]=f[T];  
              printf ("%d\n", f[n%T]);  
        }     
        return 0;  
    }   

 

代码二：

/*记得当时刚学，不会这种高级方法，大神在旁边看了一眼，直接给构造了一个矩阵，交了我幂取模，满满的崇拜和感谢
刚开始学，朋友不多，有人教一个东西，感觉真幸运，自学可能又要好久吧*/

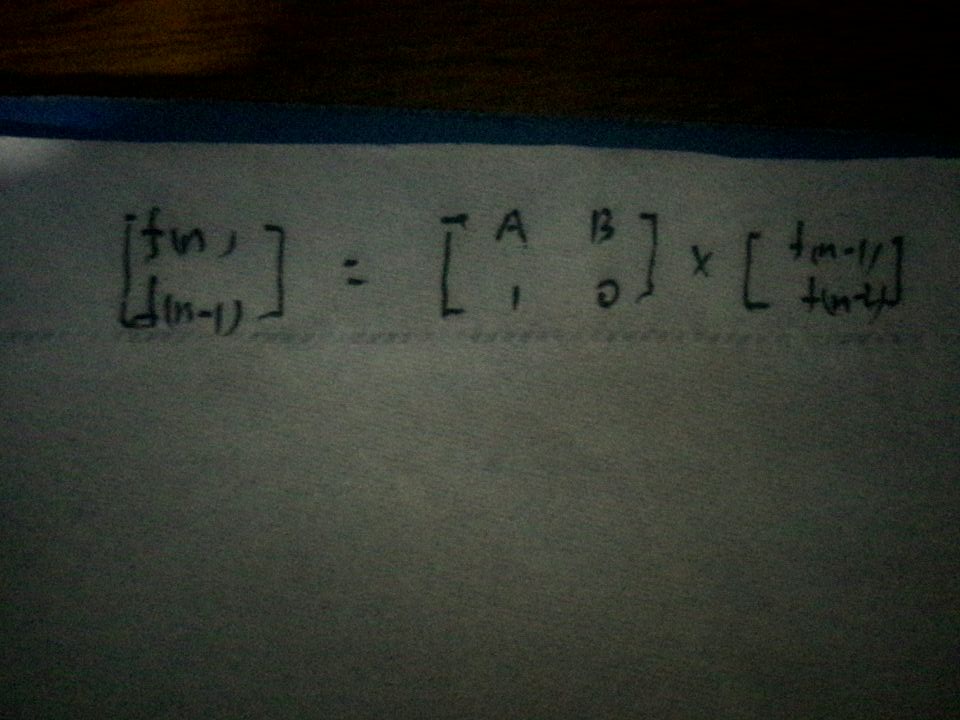
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct matrix{
    int Q[10][10];
};
matrix mult_pow(matrix a,matrix b){//矩阵乘法
    int i,j,k;
    matrix c;
    memset(c.Q,0,sizeof(c.Q));
    for(i=1;i<=2;i++)
        for(j=1;j<=2;j++)
            for(k=1;k<=2;k++)
                c.Q[i][j]=(c.Q[i][j]+a.Q[i][k]*b.Q[k][j])%7;

    return c;
}

matrix mult_pow_mod(matrix a,int n){
    matrix ret;//构造矩阵
    ret.Q[1][1]=1;
    ret.Q[1][2]=0;
    ret.Q[2][1]=0;
    ret.Q[2][2]=1;
    while(n){//快速密取模
        if(n&1) ret=mult_pow(ret,a);
        a=mult_pow(a,a);
        n/=2;
    }
    return ret;
}

int main(){
    int a,b,n;
    while(cin>>a>>b>>n){
        if(a==0) break;
        if(n<=2) {
            printf("1\n");
            continue;
        }
        matrix A;//构造矩阵
        A.Q[1][1]=a;
        A.Q[1][2]=b;
        A.Q[2][1]=1;
        A.Q[2][2]=0;
        A=mult_pow_mod(A,n-2);
        printf("%d\n",(A.Q[1][1]+A.Q[1][2])%7);
    }
    return 0;
}