一、极限总结
第一章、极限的求解
在本次文章中，将分享我个人在刷完部分极限求值的题目后的心得体会，希望能在总结中得到更深的体会。
1. 前言
在极限的求解过程中，我们普遍会有如下顺序，a. 判断是否可以用带入求出极限值。b. 运用等价无穷小能否进行第二轮化简。c.实在没办法，看是否能化为可以洛必达的形式，再洛一下。
但其实，我们在进行等价无穷小化简的时候，可以适当的运用泰勒展开式来进行化简，因为其实等价无穷小就是一阶泰勒展开等价。
请记住下面的这几个常用的展开式，将在接下来的题目中经常用到，也确实十分好用。
2.习题详解）
由于题目实际上是无法全部列举的，所以我只举例几种我认为的典型题目。
2.1
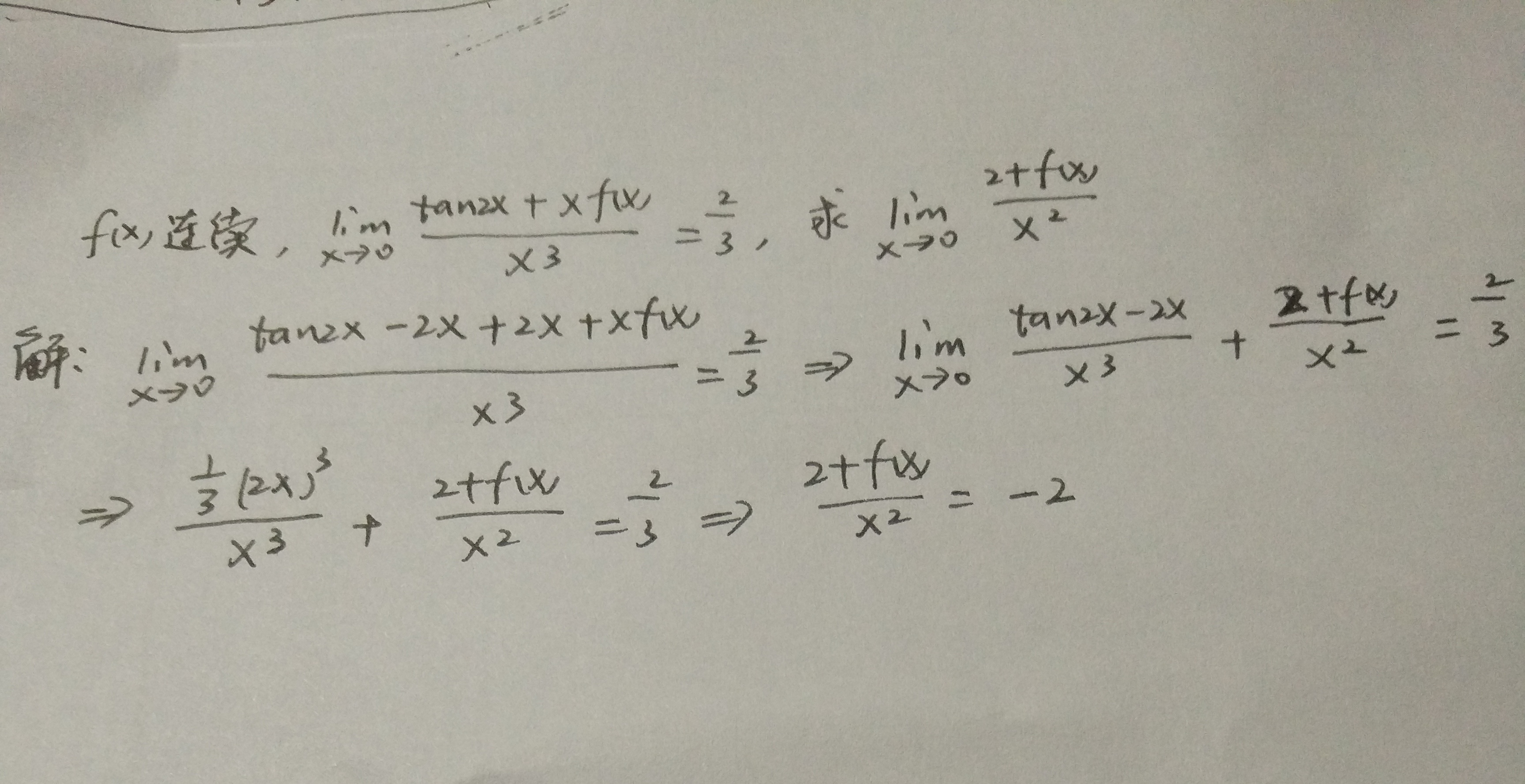
我们看到，这是一题构造题，本质是，我们要将要求的结果在原来的式子当中展示出来，然后再求分极限，我们在仔细看分部极限当中有一步tan2x-2x/2^3，我直接得出 1/3(2x)^3 /x^3，可能有人会觉得奇怪，我怎么直接的出来的？因为正常而言，这个需要我们洛必达，洛一下，一下出不来，就洛两下。但是实际上，使用泰勒展开式，一步就可以到位了。tan(2x)=2x+(2x) ^3 /3!+o(x^3)。
2.2
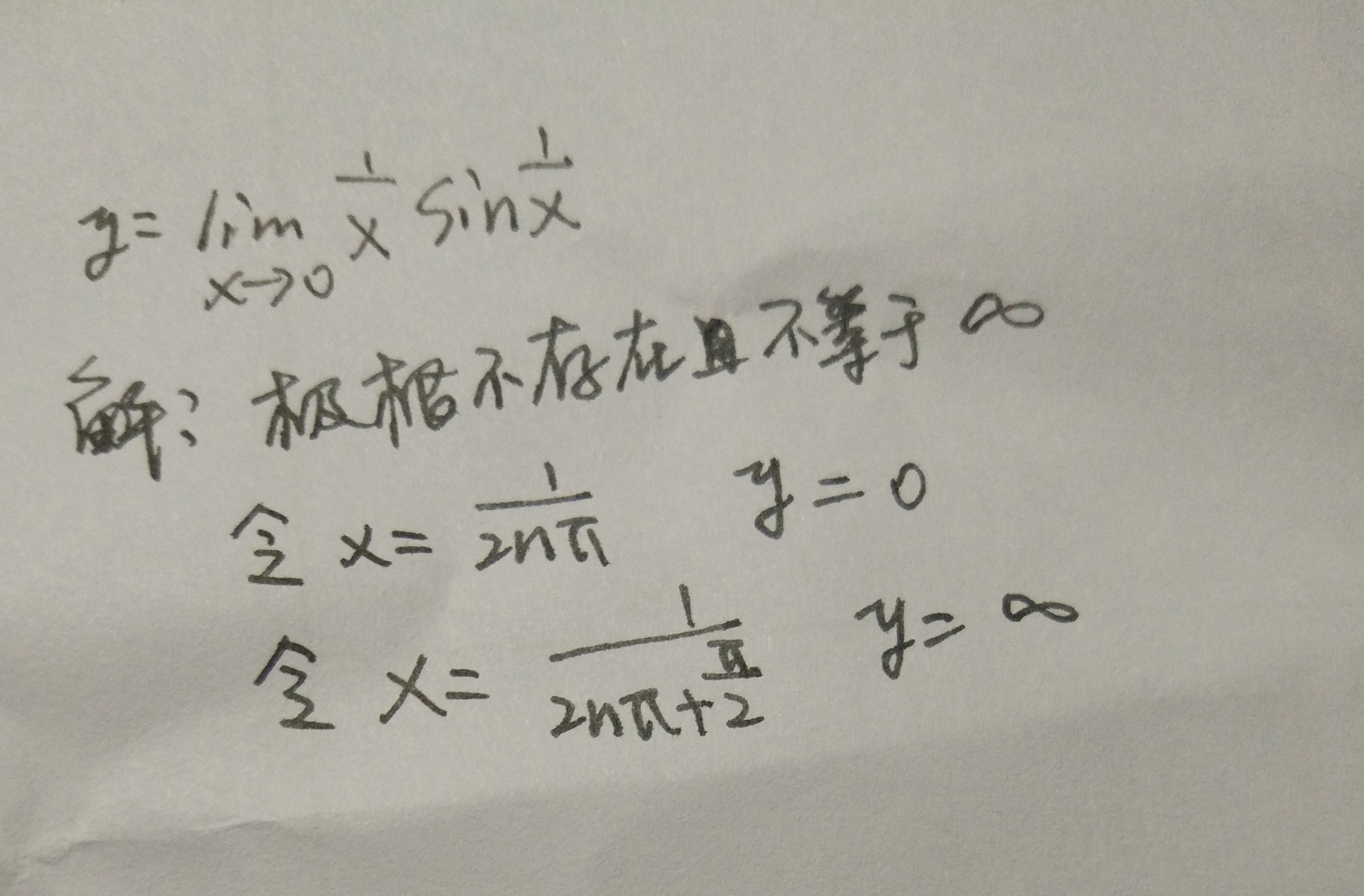
实际上，我们通过函数的正负性可以快速得到答案，在1/x趋于无穷大时，sin(1/x)是正负在变换的，也就肯定没有极限。但从这题，我想说的是，有些题目，举例子做反证法是很有用的，其次，这个题目，很容易和1/x * sinx,x趋于无穷大弄混，后者是标准的无穷小乘以有界函数。
2.3
我们可以看到这一题，存在两个知识点，一是隐函数的求导，二是导数的定义。 隐函数求导，我们可以利用两边同时对x求导，然后用链式求导法则求出来，或者我们直接可以用偏导的知识令f(x,y)=0，对两边的x求导得到可以得到隐函数的求法。
更为重要的是，这道题目提醒我们，在求极限的时候，要时刻记得是否与函数的求导形式类似。
2.4
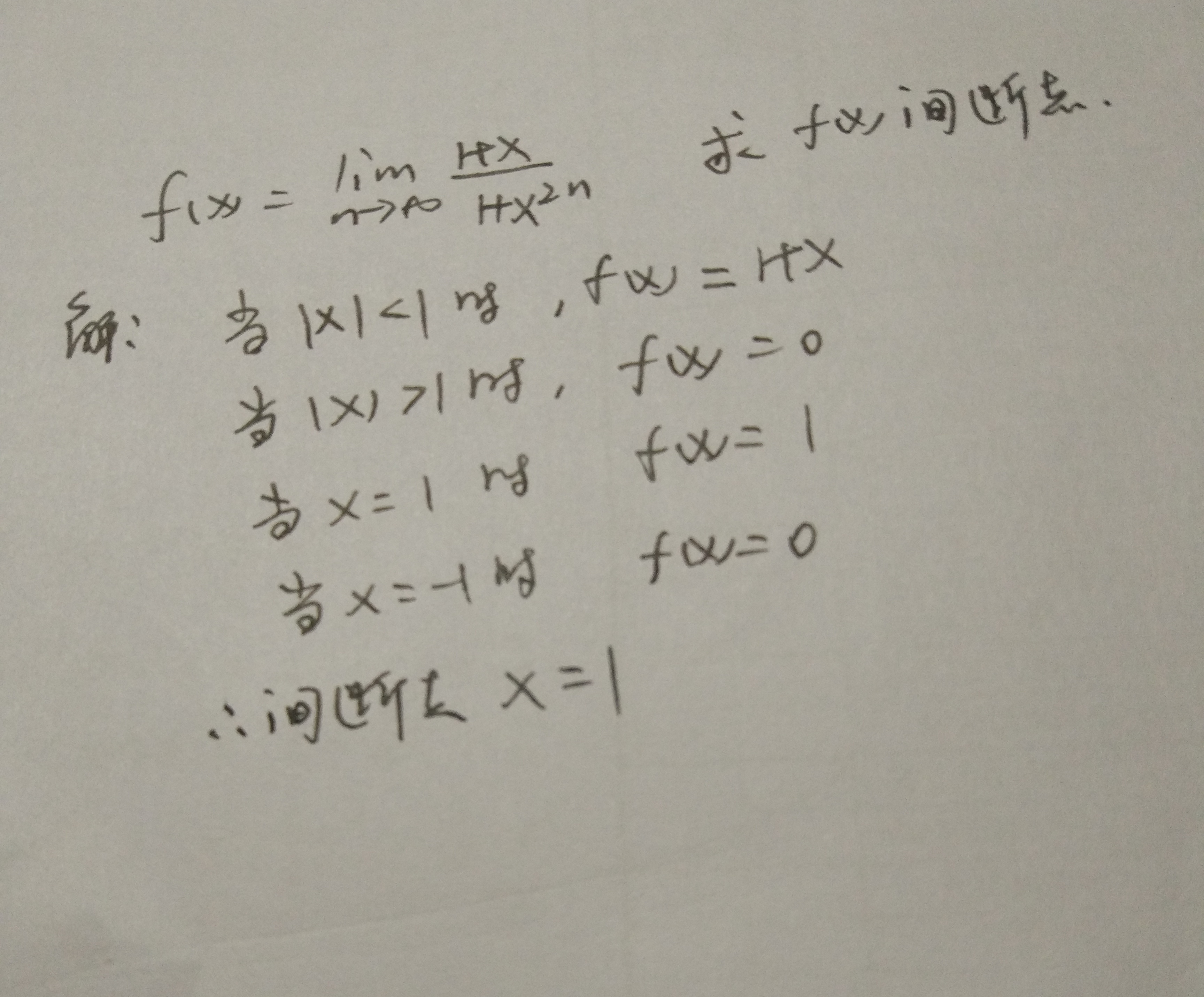
这道题，题目其实很简单，注意点只有一个,就是要对x^(2 * n)要加以考虑,考虑其在无穷时的多样性。
2.5
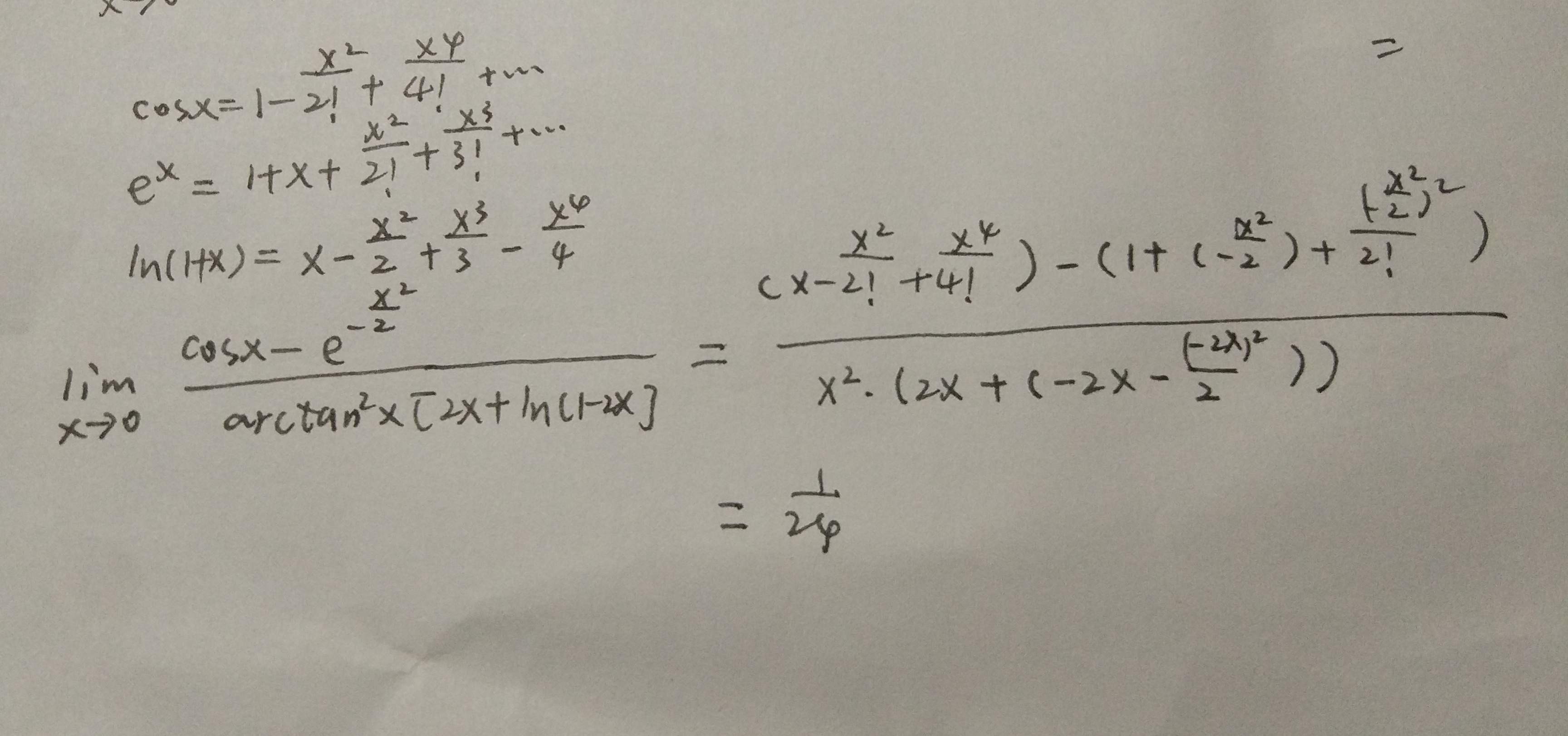
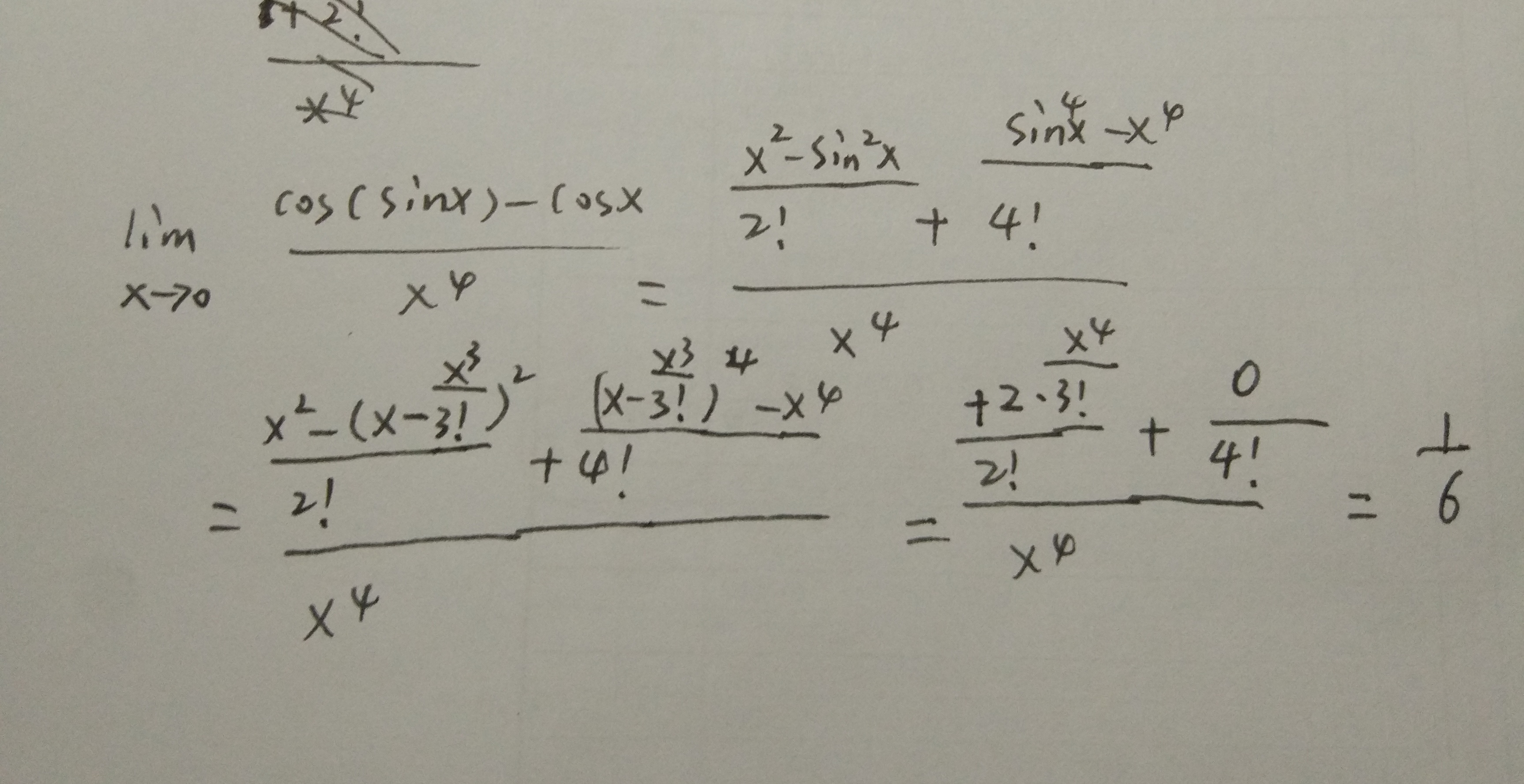
这些题，可以淋漓尽致的展现用泰勒展开在求极限的万能以及方便之处，能将复杂的式子瞬间简化。我们看到，在三角函数的嵌套中使用最为方便，以及三角函数的加减中灵活使用也很便利。其实利用函数在x=0处的泰勒展开，并带有皮亚诺余项的公式，可以化简得到更多的“等价无穷小”,例如ln(1-x)+x就可以等价于-x^2/2，以及 e^ (x^2)-cosx。
2.6
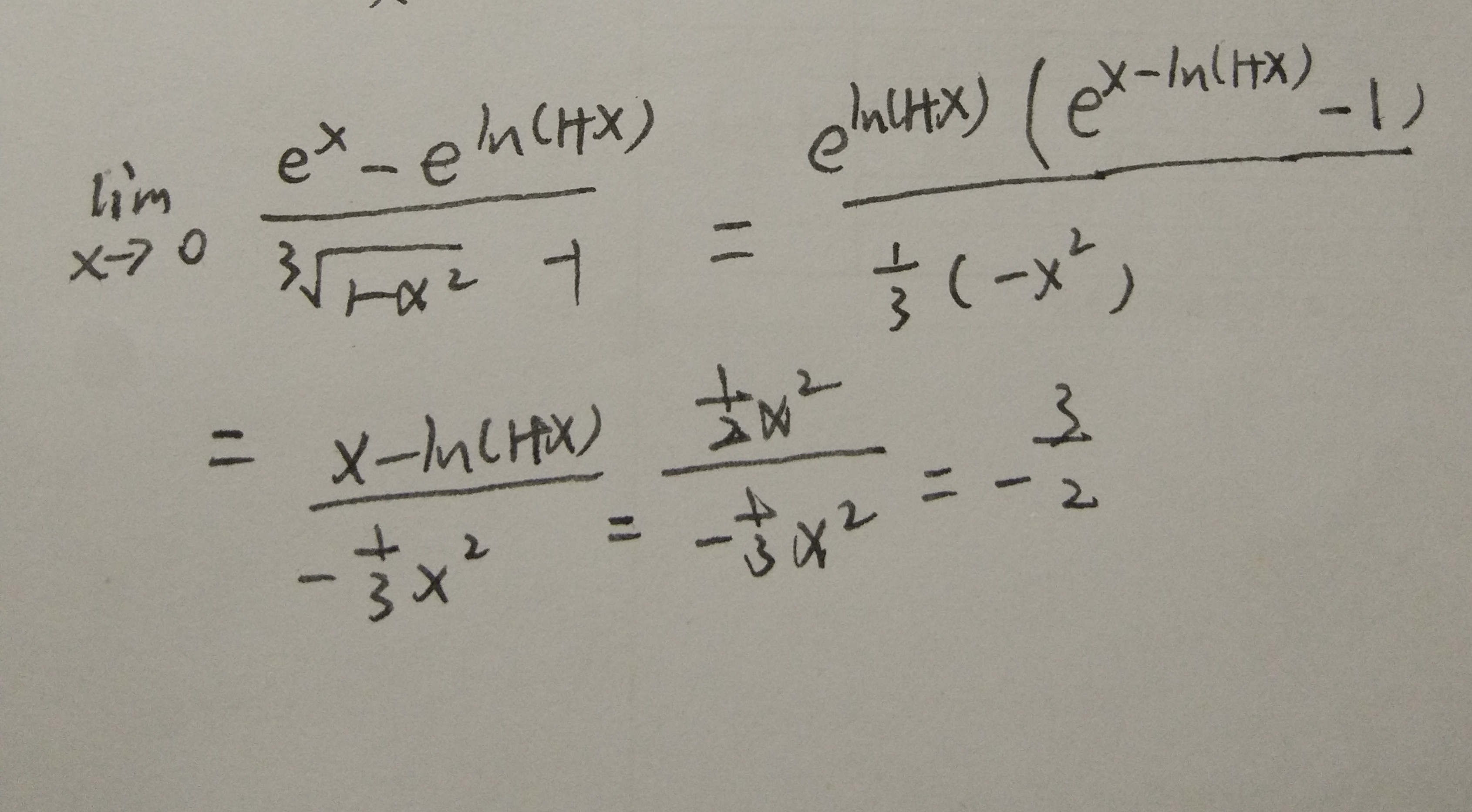
这一题，用到一个简单的泰勒展开ln(1-x)+x就可以等价于-x^2/2，可以加快点速度，但实际上这一题的重点是对于以e为底的指数，或者说任何指数，我们需要首先思考两件事，第一，能否提出公因项然后化为可用等价无穷小的形式，第二，能否直接先用泰勒展开简化。等到实在没办法，才寻求洛必达。
2.7
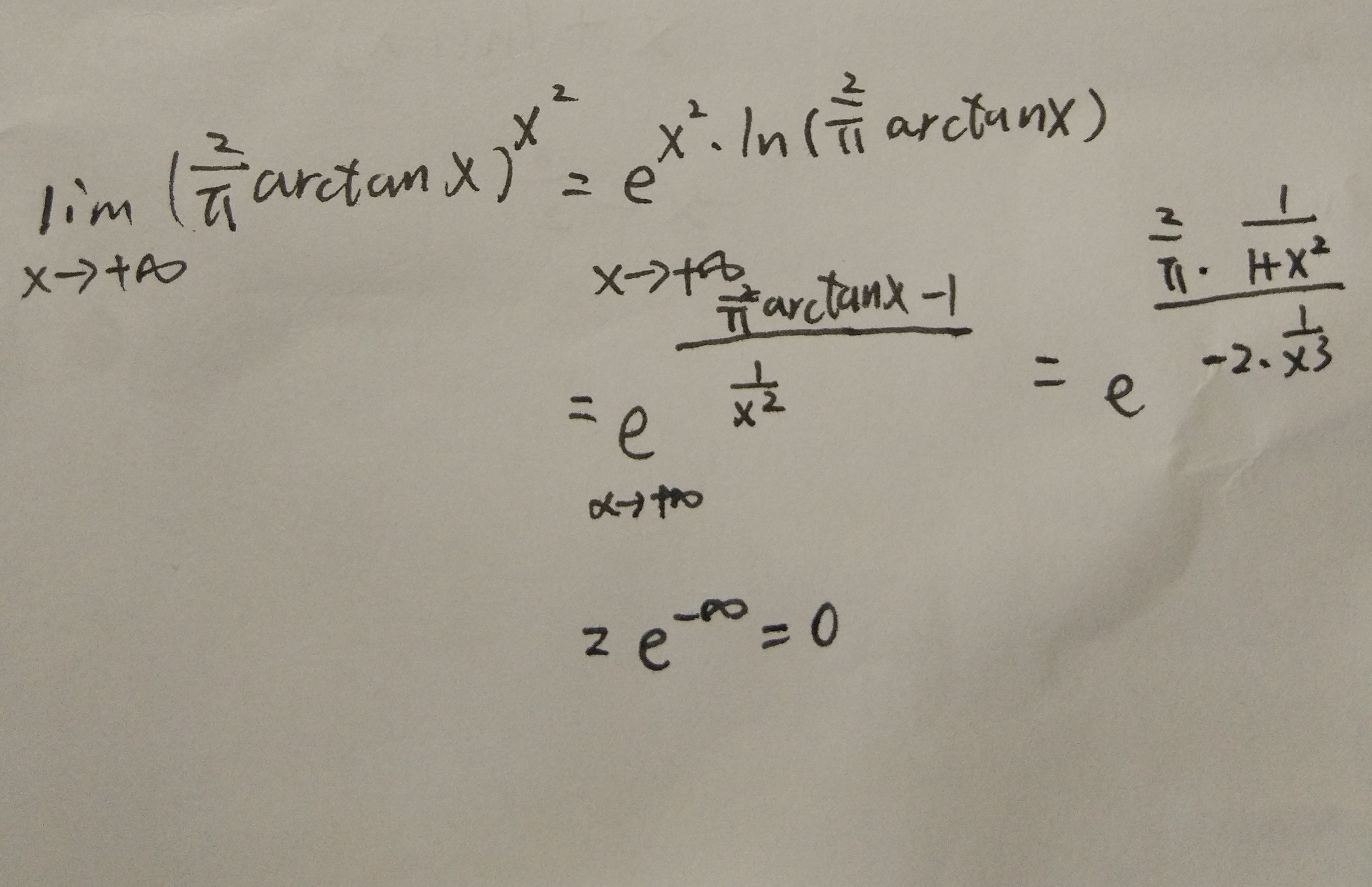
这一题很简单，普通的等价无穷小替换，再加上洛必达洛一下就出来了。但我之所以选择这一题的原因是这题目告诉我们，当部分极限不存在的时候，不代表整体极限不存在。以及写公式要写全，因为有人会把题目两边取对数，然后求出来是负无穷，就觉得没有答案。
2.8
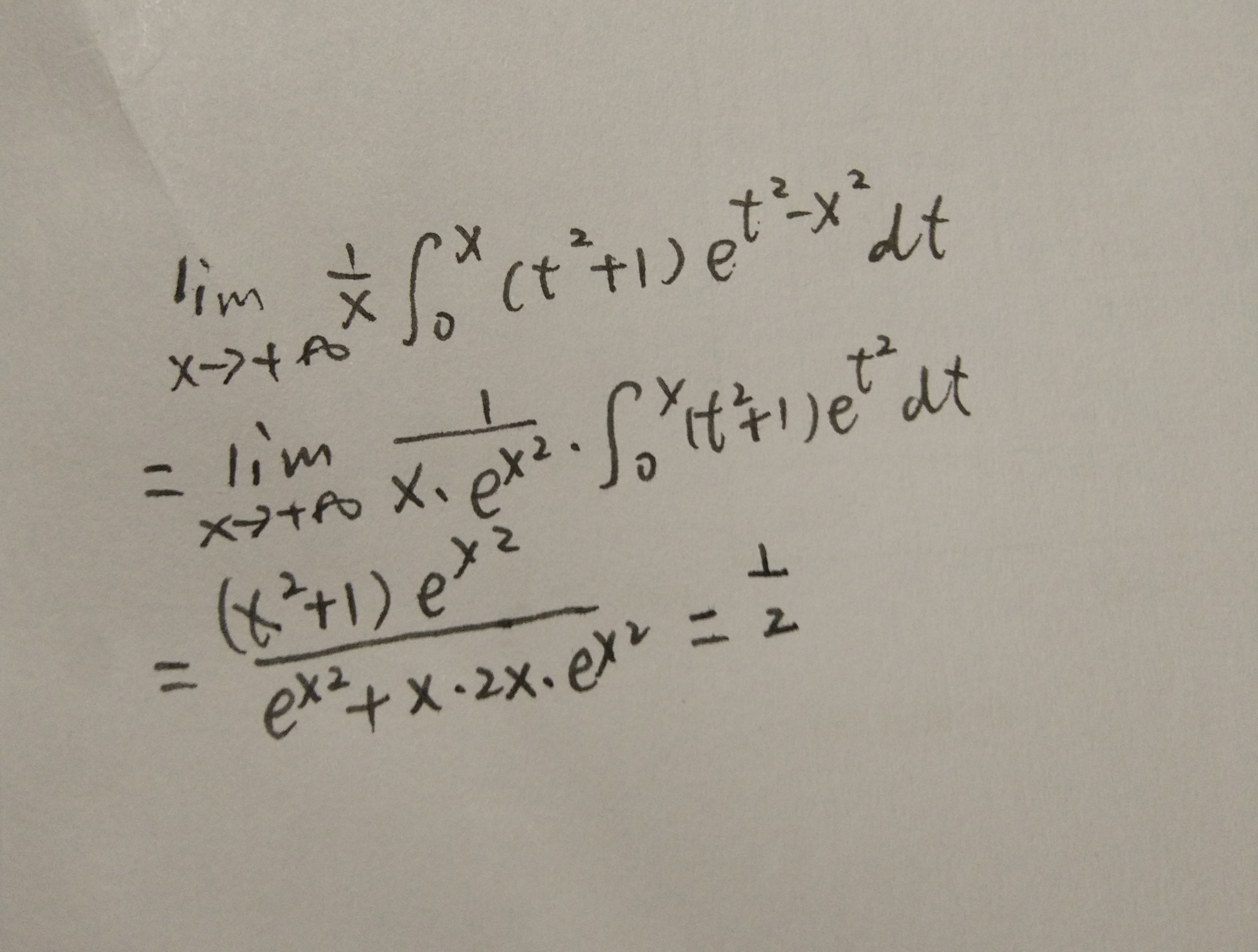
这一题难度也小，但是需要提醒的点是在存在积分表达式的情况下，一定要把常数先提出来，这样子整个表达式会变得好看很多。存在被积表达式，一先看常数是否可以提取，而看是否可以换元得到更好看的积分形式。
2.9
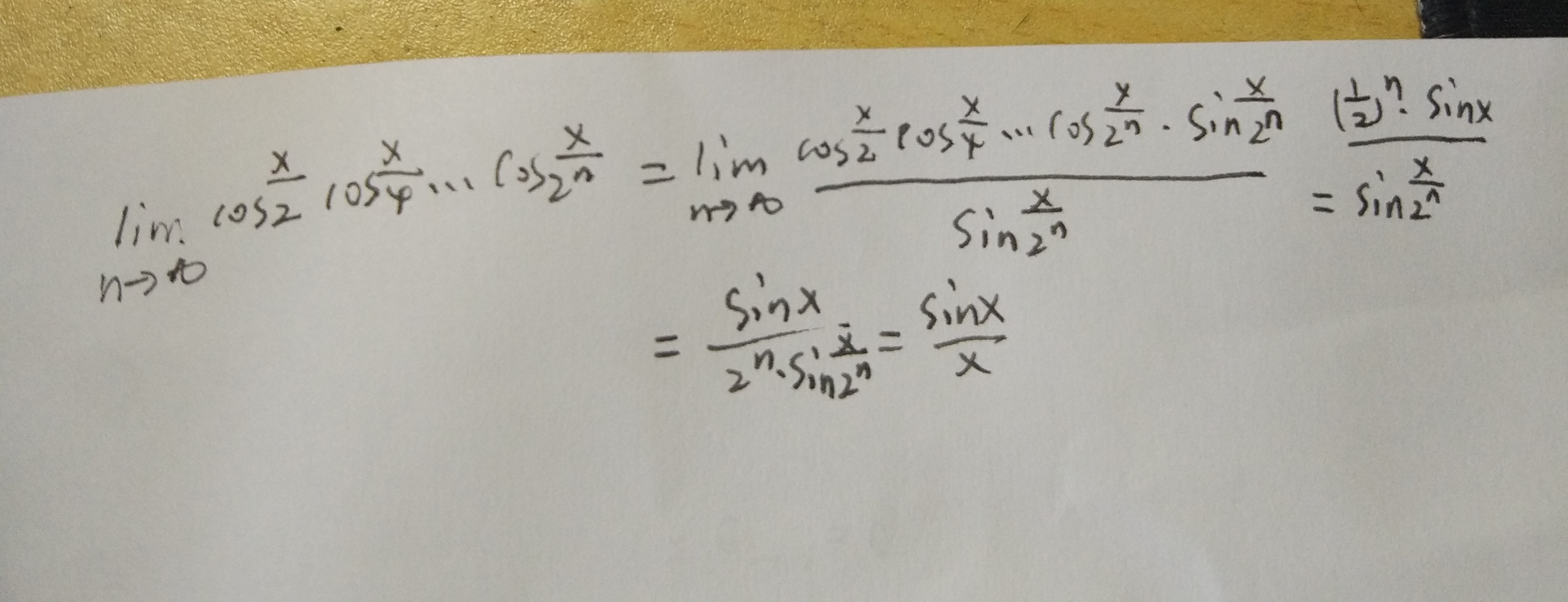
这两题展示了基本的三角函数化简方法。其实三角函数的化简方法要求我们掌握和差化积，积化和差。简单的说明，和差化积其实需要看，是什么和差，将a和b转化成，(a+b)/2+(a-b)/2，(a+b)/2-(a-b)/2，进行展开，根据三角函数展开公式，也就意味着只有s+s，c+c可以化简，如果是s+c的化，可以利用取系数的平方和来构造sc+cs类型。
如果是积化和差，就是利用和差化积的逆向，看是否是sc，cs，cc，ss选择相应的公式。
2.10
在这几题中，我们看到，对于数列求极值，首先观察是否可以换成积分表达式，其次观察是否可以用夹逼准则。
我们看到使用夹逼准则可以取前取后，或者分子/分母取前后。还有重要的是对数可以把乘除换成加减法。
2.11
最后，我们来看一下这几道题，其实思路都是相似的，利用数列极限相同，可以得到二次方程求解。其中要证明数列极限存在，可以用数学归纳法。
以及介绍一个好用不等式（ln(1+x)<x<e^x-1）。
Summary
这是第一次尝试以博客的形式写自己的学习笔记，在这个年代电子版的存在会更久远吧。展望接下来九个月的时间，我都将在每一次阶段复习之后，都写下博客来记录。以方便后面自己查看。
对于本次阶段复习，过了一遍极限的求解方式。得到了一下重要的体会：
- 先带入计算是否能求极值。
- 利用等价无穷小（或者化为等价无穷小形式）化简
- 利用泰勒展开化简。
- 实在不行，再用洛必达。
关于数列
- 观察是否是可以化为被积函数形式。
- 观察是否可以利用分子分母的缩小与放大进行夹逼准则求解。
- 利用几个不等式进行夹逼准则。
