最短路径之差分约束
一、前言
本文的目的是探讨最短路径与差分约束之间的关系。为了方便理解,本文将从存储图的数据结构,最短路径的算法,以及最短路径算法和差分约束之间的相互转换关系来讨论。而基于最短路径的有一个著名的三角形不等式,即两边之和大于第三边或者两边只差小于第三边,a+b>c和a-b<c。
- 图的存储结构
工欲善其事必先利其器,为了更好的理解最短路径,必须先了解存储图的数据结构。
一般而言,图的存储方式,有按节点存储按边存储两种方式。
- 传统来说,按节点存储的是临接矩阵存储方式,优点是实现简单,一个二维数组就能实现。但缺点也很明显,需要O(n^2)的存储空间。
/*
*a[i][j]代表的是以i为起点j为终点的边的权值。
*一般而言的初始化是先让要初始化的每个节点都为无穷大。然后再输入。
*/
int a[N][N];
- 可是在大部分情况下,我们的边数远远没有打到O(n^2),这种情况下,我们可以选择按边存储。按边存储的主要存储方式是邻接表,前向星,以及链式前向星。
/*
*邻接表是为每个节点建立好边的关系,将与每一个定点连接的边连成一个链表。
*在C++中,有为我们封装好的list链表,可以直接使用。
*
*/
list<int> li[N];
/*
*前向星也是按边存储,通过构造结构体节点,存储每一条边的开始节点,终止节点,和边权值。
*再将所有节点数组按照开始节点的大小进行排序,就可以达到连续访问从一起点出发的边。
*但同时缺点也明显,需要进行一次排序,开销也比较大。
*/
struct edge{
int u,v,w;
edge(){}
edge(int _u,int _v,int _w){
u=_u;
v=_v;
w=_w;
}
}
edge eg[N];
bool cmp(edge a,edge b){
return a.u<b.u;
}
sort(eg,eg+N,cmp);
/*
*链式前向星按照我的理解,就是以数组的方式构造链表。
*每条边的next都是指向上一条以相同节点开始的边。
*head[u]指向的总是以u开头的最后一条加入的边的地址。
*/
struct edge1{
int u,v,w,next;
edge(){}
edge(int _u,int _v,int _w,int _next){
u=_u;
v=_v;
w=_w;
next=_next;
}
}
edge eg[N];
void addedge(int u,int v,int w){
eg[count]=edge1(u,v,w,head[u]);
head[u]=count++;
}
/*
*其实根本不用这么复杂的结构,c++提供给了我们vector容器。
*/
vector<edge> eg[N];
eg[u].push_back(edge(u,v,w));
- 最短路径算法
聊完了基本的数据结构,既然本文是介绍最短路径之差分约束,接下来就讲介绍最短路径的算法。最短路径的算法一般而言,是分为两种,一种是正权边,一种是存在负权边。
- 正权边,使用的是dijkstra算法,为了优化,一般加入优先队列进行使用。
/*
*节点的数据结构
*id代表节点的编号,value代表源点到这点的当前最短距离
*/
struct node{
int id;
int value;
node(){}
node(int _id,int _value){
id=_id;
value=_value;
}
bool operator < (const node &a)const{
return value>a.value;
}
}
struct edge{
int u,v,w;
edge(){}
edge(int _u,int _v,int _w){
u=_u;
v=_v;
w=_w;
}
}
vector<edge>eg[N];//存储边,利用vector实现链式前向星。
bool vis[N];//该节点是否已经属于扩展过的,是就是true,否就是false。
int pre[N],dist[N];//pre[i]存储到i的上一个节点,dist[i]存储源点到i的当前最短距离。
void dijkstra(int s){
priority_queue<node> que;
que.push(node(s,0);
while(!que.empty()){
node temp=que.front();
int u=temp.id;
que.pop();
vis[u]=true;
for(int i=0;i<eg[u).size;i++){
int v=eg[u][i].v;
int w=eg[u][i].w;
if(!vis[v]&&dist[v]>dist[u]+w){
dist[v]=dist[u]+w;
pre[v]=u;
que.push(node(v,dist[v]);
}
}
}
}
void init(){
for(int i=0;i<n;i++){
vis[i]=false;
dist[i]=INF;//INF表示为不可达
eg[i].clear();
}
}
- 而当图中存在负权边时,就需要使用,bellman-ford算法或者spfa算法,下面我们将介绍spfa算法,可以将其视作是bellman-ford算法的优化版本。
/*
*
*/
struct node{
int id;
int value;
node(){}
node(int _id,int _value){
id=_id;
value=_value;
}
bool operator < (const node &a)const{
return value>a.value;
}
}
struct edge{
int u,v,w;
edge(){}
edge(int _u,int _v,int _w){
u=_u;
v=_v;
w=_w;
}
}
bool inq[N];//标记定点是否在队列中,true表示在,flase表示不在
vector<edge> eg[N];//用vector来模拟链式前向星,或者说邻接表
int dist[N],visitcount[N];//dist[i]记录从源点到i的当前最短距离,visitcount[i]表示i节点被访问的次数;
void spfa(int s,int n){
for(int i=0;i<=n;i++){
inq[i]=0;
visitcount[i]=0;
}
priority_queue<node> que;
que.push(node(s,0));
inq[s]=1;
while(!que.empty()){
node temp=que.front();
int u=temp.id;
que.pop();
inq[u]=0;
viscount[u]++;
if(visitcount[u]>n){
cout<<"No answer!"<<endl;
}
for(int i=0;i<eg[u].size();i++){
int v=eg[u][i].v;
int w=eg[u][i].w;
if(dist[v]>dist[u]+w){
dist[v]=dist[u]+w;
if(!inq[v]){
que.push(node(v,dist[v]));
inq[v]=true;
}
}
}
}
}
二、差分约束
1.差分约束的定义
如若一个系统由n个变量和m个不等式组成,并且这m个不等式对应的系数矩阵中每一行有且仅有一个1和-1,其它的都为0,这样的系统称为差分约束( difference constraints )系统。
即可以化为:
x[i]-x[j]<=ak
x[c]-x[d]>=ak1
...
x[n]-x[p]<=akn
也就是说,差分约束,就是一组不等式的集合。同时我们观察,我们用来求最短路径的方程,dist[u]> dist[v]+w,通过移项,可以看到,和差分约束的方程相同,实际上,我们可以把x[i]-x[j]<=ak看作是,从节点j指向节点i的一条边为ak的有向图。于是通过多个不等式的集合,我们可以相应的建出有向图。例如下图:
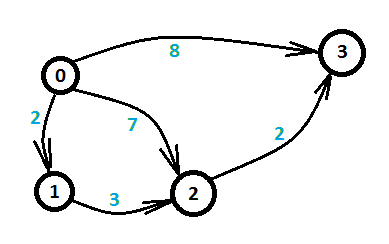
同时,我们可以从上面的介绍中看到x[i]-x[j]<=ak,x[i]-x[j]>=ak都是从i到j的一条边,边值是ak,但是有什么区别吗?
- x[i]-x[j]<=ak,表示的是每一条边,都小于ak,所以我们可以看到,例如上图从0->3的路有三条,0->2->3 路径长度L1, 0->3路径长度L2,0->1->2->3路径长度L3三条路。
- 所以实际上,不管我们怎么到达,都得满足全部约束,所以x[3]-x[0]<=min(L1,L2,L3)。也就是意味着,当我们在求从0到3的最短路径,就是在求满足约束情况下的最大值。
- x[i]-x[j]>=ak,与上面相反,所得的实际结果应该是都大于每一条边,所求的x[3]-x[0]>=max(L1,L2,L3),所以求0到3的最长路径,就是求得在满足约束条件下的最小值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号