算法学习笔记——感知机原理及其代码实现

感知机原理及代码实现

上篇讲完梯度下降，这篇博客我们就来好好整理一下一个非常重要的二分类算法——感知机，这是一种二分类模型，当输入一系列的数据后，输出的是一个二分类变量，如0或1

1. 算法原理

1.1 知识引入

说起分类算法，博主想到的另一个算法是逻辑回归，而感知机从原理上来说和回归类算法最大的区别就是引入了几何的思想，将向量放到了高维空间上去想象。首先介绍一个概念——超平面(hyper plane)，超平面就是比当前维度还少一个维度的数的集合。打个比方，如果是二维平面，那么超平面就是一维平面，也就是一条直线，形象地来想象，就好比是一条线切割了一张纸，并将一张纸上标记为1和标记为-1的点给分开来了；类比到三维空间，其超平面就是一个二维平面去切割一个立方体，好，下面开始进行原理的数学推导：

高中学数学的时候我们就知道，二维平面上的一条直线内的点可以用一般方程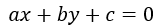来表示，那么该二维平面中，满足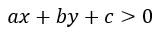的(x, y)表示在此一般方程上方的点，而满足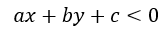的点则表示在此一般方程下方的点，将此情形推广到高维空间如n维空间(过高维度我们将无法直观想象)，就可得到一超平面方程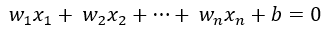，那么推导后可知，满足等式左边>0的点自然就在该超平面的上方，<0的点就在该超平面的下方，自然，用这种方式将所有点分成了两类，因此，原问题就转换成了找到这么一个超平面将被点分成两类的问题了，将该方程写成两个向量相乘再加上一个常数项，或称截距项的形式，就可得到下式：

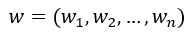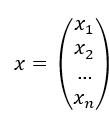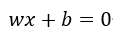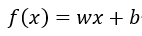令，，则原式可转换为：，现令，并令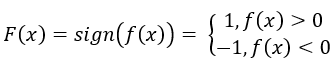，则F(x)函数可以用来做线性分类器。

1.2 推导过程

上面的式子得到之后，我们就要想，该如何求得w和b的值呢？模仿博主上两篇博客里的套路，那自然是分三步走咯，先随机设置w和b的初始值，然后写出一个损失函数(又称成本函数)，最后使用梯度下降法通过不断迭代求得最优解使得损失函数最小。依照这个想法，第一个容易想到的思路就是既然我们的目标是要找到一个超平面方程正确无误地将两类点彻底分开，那么最优的解自然就是使得错误分类的点降到0个就行了呗，但是该方法有一个明显的缺点，函数值若是一个两个的话，就是分类变量了，其函数图像并不连续，因此第三步梯度下降我们没法用！于是第二个思路应运而生，既然我们要让函数连续，我们将求点的个数转换成误分类点到超平面方程的距离之和不就行了吗？那下面，我们首先推导点到直线的距离公式：

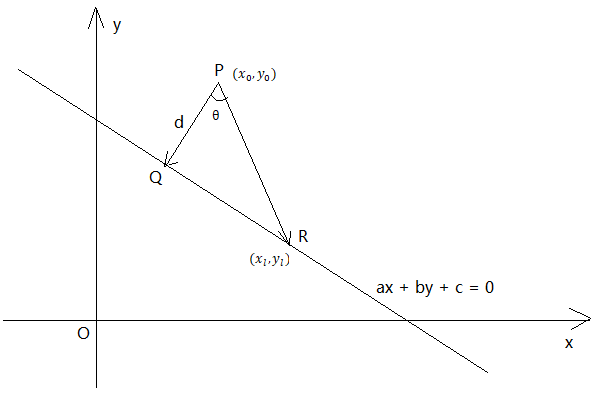
 在二维直角坐标平面XoY内，有一直线方程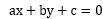，现需要求的是向量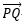的模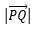即d的长度：

首先推导d的公式：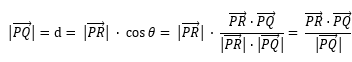

设R点的坐标为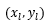，既然R点在直线上，那么必满足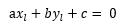：，可推出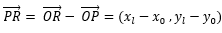

通过原方程可轻松计算出方程的斜率为(-b, a)，那么与该方向垂直的向量通过点积为0的原理可算出是(a, b)，如此一来，公式中的两个关键向量都已经计算出来，现在开始代入公式

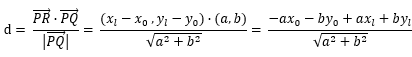，然后带入等式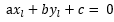并整理，可得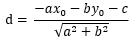，由于距离比为正数，加上绝对值符号，最终等式为：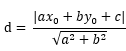

至此，二维平面上的推导过程告一段落，现在将其扩展至高维空间，也就是计算误分类点到超平面的距离，类比上式，可得：

设误分类点的集合为M，则损失函数L的公式为：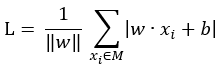

下一步为对上面的损失函数求导，分两步，求函数对w的偏导数，以及函数对b的偏导数，求出后运用梯度下降迭代即可，然而，对含有绝对值的函数求导绝非易事，因此需要通过某种方式想方设法去除绝对值符号，

 

 注意到，对于正确分类点来说，正类标记为1，负类标记为-1，而正类位于超平面上方，负类位于超平面下方，因此对于正确分类点，必有不等式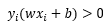，那既然所有的点只能区分为正确分类点以及误分类点，那么对于误分类点就必有不等式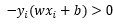，就是一个负负得正的道理，这样一来，绝对值符号可以去除，原式就变为了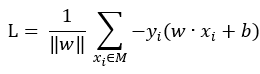：，我们的目标就是求这个函数的最小值即可。至此，已经可以给出两个偏导数的计算公式了：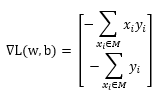

下面开始简单写一下梯度下降的伪代码：

1. 选定一个系数向量和截距的初值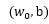

2.在训练集中进行遍历，逐个选取

3.遍历过程中，如果出现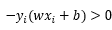的点，那就说明该点是误分类点，这时就需要更新初值了，设步长为λ，则更新函数为：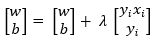

4.重复2、3两步，直到整个数据集没有误分类点，即可说明线性分类器已经找到

2.代码编写

下面给出上述算法的python代码实现，并将代码封装成了一个类，这个类中定义了两个不同的梯度下降代码实现，分别为批量梯度下降以及随机梯度下降：

import numpy as np
import pandas as pd
import random
from sklearn.datasets import make_blobs

class perceptron:
    
    def __init__(self, sample_size = 200, centers = [[1,1],[3,4]], cluster_std = 0.6):
        X,Y = make_blobs(n_samples = sample_size, centers = centers, cluster_std = cluster_std, random_state = 11)
        Y[Y == 0] = -1
        self.X = X
        self.Y = Y
    
    def BGDfit(self, w, b, lam):
        #This function aims to use Batch Gradient Descent algorithm to find the most suitable function
        while True:
            x_mat = np.mat(self.X)
            tmp = np.ravel(x_mat * w + b) * self.Y
            if sum(tmp < 0) == 0:
                break
            tmp_X = np.array(self.X[tmp < 0])
            tmp_Y = np.array(self.Y[tmp < 0])
            tmp_Y_final = np.column_stack((tmp_Y, tmp_Y))
            w = w + lam * np.mat((tmp_X * tmp_Y_final).sum(axis = 0)).T
            b = b + lam * sum(tmp_Y)
        return w, b
    
    def SGDfit(self, w, b, lam):
        #This function aims to use Stochastic Gradient Descent algorithm to find the most suitable function
        missing_index = 0
        while missing_index != -1:
            missing_index = -1
            for i in range(self.X.shape[0]):
                if self.Y[i] * (np.dot(w, self.X[i]) + b) < 0:
                    missing_index = i
                    break
            if missing_index != -1:
                w = w + lam * self.Y[missing_index] * self.X[missing_index]
                b = b + lam * self.Y[missing_index]
        return w, b

3.感知机的对偶形式

3.1 原理

使用原始的感知机形式时，在遇到处理海量数据的场景时，运算速度会十分缓慢，那么，存不存在一种方式，我们可以预先将某些矩阵计算好，将其缓存起来而不必每次都进行重复的运算呢？答案是肯定的，这就是感知机的对偶形式，下面开始正式介绍：在1.2章节的时候给出过w和b的更新函数，每遇到一个误分类点，就将w进行更新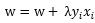：，将b进行更新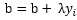：，我们可以从中总结出这样一个规律，那就是，每遇到一个误分类点一次，就在w基础上多累加一次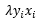，在b基础上多累加一次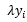，在式子中，λ是确定的，特征值数据集是确定的，特征值对应的分类也是确定的，唯一不确定的就是我们不知道何时会遇到误分类的点，因此，不确定的变量是误分类次数，那么，感知机的对偶形式呼之欲出，我们只要维护一个误分类次数的数组，每当遇到误分类点的时候，在该数组的对应位置上进行累加即可！

设数据集中一共有n个点，并设误分类点次数向量为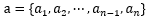，根据上面的思路，w和b就可以写成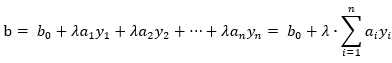，，，我们将w的初始值设置成零向量，那么w就变成了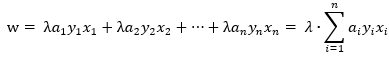：，将这个式子代入至判断某个点是否是误分类点的判别式中，如果是误分类点，那就更新a和b，具体的伪代码如下：

1.选定a和b的初始值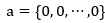：，b = 0

2.在训练集中进行遍历，逐个选取

3.如果发现某个点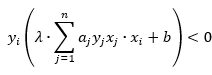，那就更新a和b，，

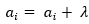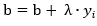
4.重复2、3步直到没有误分类点，算法停止

3.2 代码实现

下面给出感知机对偶形式的python代码实现，使用的是随机梯度下降法：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import random
from sklearn.datasets import make_blobs

sample_size = 200
centers = [[1,1], [3,4]]
X, Y = make_blobs(n_samples = sample_size, centers = centers, cluster_std = 0.6, random_state = 11)
Y[Y == 0] = -1
gram = np.array(np.mat(X) * np.mat(X).T)
a = np.zeros(X.shape[0])
b = 0
lam = 0.1
count = 0
while True:
    count += 1
    missing_index = -1
    for i in range(X.shape[0]):
        checking = Y[i] * ((a * Y * gram[i, :]).sum() + b)
        if checking <=0 :
            missing_index = i
            break
    if missing_index == -1:
        break
    a[missing_index] += lam
    b += lam * Y[missing_index]
theta = np.ravel(np.mat(a * Y) * np.mat(X))
theta, b