【6】线段树学习笔记
前言
太菜了,现在才写线段树的学习笔记。
由于线段树学习历时较长(大约 \(1\) 年),码风可能会严重不协调。以后我的线段树码风以线段树讲解板块为准。
长文警告:本文一共 \(1495\) 行,请合理安排阅读时间。
UPD on \(2025.6.30\):新增了线段树二分的内容。
线段树
线段树是一种基于分治思想的二叉树结构,用于统计区间信息。与树状数组相比,线段树是一种更加通用的结构。
\(1\):线段树每个节点代表一个区间。
\(2\):线段树具有唯一的根节点,代表的区间是整个统计范围 \([1\sim n]\)。
\(3\):线段树每个叶节点都代表一个长度为 \(1\) 的元区间 \([x,x]\)。
\(4\):对于每个非叶节点 \([l,r]\),它的左儿子是 \([l,mid]\),右儿子是 \([mid+1,r]\),其中 \(mid=\lfloor\frac{l+r}{2}\rfloor\)。每个节点维护的是 \([l,r]\) 的信息。
节点定义
我们一般用结构体来存储线段树的节点,例如下面代码。可以预处理出每个点左儿子和右儿子的编号,记作 \(lc[x]\) 和 \(rc[x]\),便于之后进行操作。
由于线段树维护的信息多种多样,这个定义可以依据题目需求进行更改,之后的线段树题目中将以此为一个讲解点。
struct node
{
long long v,ad;
}tr[400000];
上传
在线段树中,我们需要向上传递信息。一个节点的信息由它的两个子节点信息合并得到。我们可以把这一过程单独写入一个函数,便于之后进行操作。
由于线段树维护的信息多种多样,这个函数可以依据题目需求进行更改,之后的线段树题目中将以此为一个讲解点。
以维护区间和为例,很显然,区间 \([l,r]\) 的区间和就是 \([l,mid]\) 的区间和加上 \([mid+1,r]\) 的区间和。
void pushup(long long x)
{
tr[x].v=tr[lc[x]].v+tr[rc[x]].v;
}
建树
按照定义,从根节点开始递归建树。注意初始化结束之后需要向上传递信息,保证每个节点都初始化。
代码中 tr[now].v=a[l] 这一行相当于进行初始化,可以依据题目需求进行更改,之后的线段树题目中将以此为一个讲解点。
以维护区间和为例,很显然,区间 \([x,x]\) 的区间和序列中的 \(a[x]\),因为这个区间中只要这一个数。
void build(long long now,long long l,long long r)
{
lc[now]=now*2,rc[now]=now*2+1;
if(l==r)
{
tr[now].v=a[l];
return;
}
long long mid=(l+r)>>1;
build(lc[now],l,mid),build(rc[now],mid+1,r);
pushup(now);
}
需要注意的是,线段树是树形结构,需要额外空间,我们一般开四倍空间避免出现错误。
单点操作
假设操作第 \(x\) 个元素,在线段树中进行递归找到 \([x,x]\) 的叶节点。
假设当前访问节点为 \([l,r]\),有如下两种情况:
\(1\):\(x\le mid\),递归访问左儿子 \([l,mid]\),因为这个元素包含在 \([l,mid]\) 中。
\(2\):\(x\ge mid+1\),递归访问右儿子 \([mid+1,r]\),因为这个元素包含在 \([mid+1,r]\) 中。
找到 \([x,x]\) 的叶节点后,直接在叶节点上操作。注意操作完成之后需要用 pushup 更新访问到的节点的信息。
时间复杂度 \(O(\log n)\)。
区间查询
假设查询区间为 \([lc,rc]\),我们在线段树中递归。
假设当前访问节点为 \([l,r]\),有如下三种情况:
\(1\):\(lc\le l,rc\ge r\),直接返回这个区间维护的信息,因为 \([l,r]\) 被完整包含在查询区间中,区间内所有的元素都会被统计,直接返回维护的信息。
\(2\):\(lc\le mid\),递归访问左儿子 \([l,mid]\),因为整个查询区间的一部分被包含在 \([l,mid]\) 中,需要继续递归求出这一部分的贡献。
\(3\):\(rc\ge mid+1\),递归访问右儿子 \([mid+1,r]\),因为整个查询区间的一部分被包含在 \([mid+1,r]\) 中,需要继续递归求出这一部分的贡献。
注意当 \(2,3\) 都满足时,需要都递归。
每次将返回值合并起来,作为该节点的返回值继续返回。
合并方式与 pushup 几乎一致,可以依据题目需求进行更改。之后的线段树题目不会专门讲解这里,因为这里的合并就是把 pushup 再写一遍,只是有时候不是返回一个完整的结构体,只返回部分内容。
可以证明时间复杂度 \(O(\log n)\),具体怎么证我不会。
以维护区间和为例,合并只需要把每次递归返回的值加起来就行了,因为 pushup 就是这么合并的。
long long query(long long now,long long l,long long r,long long lc,long long rc)
{
pushdown(now);
long long ans=0;
if(l>=lc&&r<=rc)return tr[now].v;
long long mid=(tr[now].l+tr[now].r)>>1;
if(l<=mid)ans+=query(lc[now],l,mid,lc,rc);
if(r>=mid+1)ans+=query(rc[now],mid+1,r,lc,rc);
return ans;
}
代码中出现了 pushdown,这是后面的内容,这里先不管它。
懒标记
在区间修改操作中,我们也有可能遇见 \([l,r]\) 被完整包含在修改区间中的情况。但是区间修改就不能直接返回了,需要逐一更新,而这样复杂度又会退化到 \(O(n)\),这是我们不能接受的。
如果某次修改操作中 \([l,r]\) 被修改,而在后续的操作中没有用 \([l,r]\),那逐一更新这个区间没有任何意义。
因此,我们引入懒标记。如果一个节点有懒标记,表示这个节点曾经被修改,但其子节点尚未更新。之后的操作中,如果操作到了这个区间,将懒标记下传。
这样,遇见 \([l,r]\) 被完整包含在修改区间中的情况时,就可以在这个区间打懒标记并返回,就可以降低区间修改的时间复杂度到 \(O(\log n)\)。
注意,当我们打标记时,我们需要更新这个打标记的节点维护的值。如果不更新,一方面与懒标记定义中曾经被修改矛盾,另一方面会出现一些奇奇怪怪的错误,最好还是不要这么做。
更新的过程我们可以写入 upd 函数,便于之后进行操作。
由于线段树维护的信息多种多样,更新可以依据题目需求进行更改,之后的线段树题目中将以此为一个讲解点。
以区间加法,需要维护区间和为例,如果这个区间被打上了 \(k\) 的懒标记,那么这个区间中的每一个数都增加了 \(k\),总和就增加了区间长度乘以 \(k\),直接更新区间和即可。区间代码中 \(now\) 为当前节点,\(k\) 为懒标记的数值。
void upd(long long x,long long k)
{
tr[x].v+=k*(tr[x].r-tr[x].l+1);
}
下传
使用懒标记,自然需要懒标记下传。根据懒标记的定义,有懒标记的节点,其子节点尚未更新,我们只需要根据这个节点的懒标记,更新这个节点的两个子节点即可。下传完之后,这个节点的子节点已经被更新,需要清零懒标记。
注意更新完子节点之后,子节点同样拥有懒标记,因为我们不能确定这个子节点是不是叶节点,这个子节点也有可能有子节点。
这里更新子节点,相当于给子节点打懒标记,需要更新子节点的值。也就是说,需要对子节点进行 upd 操作。不论题目是什么要求,这一操作的方式是确定的,之后的线段树题目不会专门讲解这里。
void pushdown(long long x)
{
tr[lc[x]].ad+=tr[x].ad,tr[rc[x]].ad+=tr[x].ad;
if(lc[x])upd(lc[x],tr[x].ad);
if(rc[x])upd(rc[x],tr[x].ad);
tr[x].ad=0;
}
我们访问任何一个节点的时候,都需要下传这个节点的懒标记。一般地,我们把下传操作写在访问某个节点的函数的最开头,以保证访问这个节点时,这个节点的懒标记已经被下传。这就是为什么区间查询和区间修改的函数最开头有 pushdown 操作,其实每一个操作之前都需要 pushdown。
区间修改
假设修改区间为 \([lc,rc]\),我们在线段树中递归。
假设当前访问节点为 \([l,r]\),有如下三种情况:
\(1\):\(lc\le l,rc\ge r\),在这个区间上打懒标记,并立即更新这个节点。因为 \([l,r]\) 被完整包含在修改区间中,区间内所有的元素都会被修改,直接打懒标记。
\(2\):\(lc\le mid\),递归访问左儿子 \([l,mid]\),因为整个修改区间的一部分被包含在 \([l,mid]\) 中,需要继续递归修改这一部分。
\(3\):\(rc\ge mid+1\),递归访问右儿子 \([mid+1,r]\),因为整个修改区间的一部分被包含在 \([mid+1,r]\) 中,需要继续递归修改这一部分。
注意当 \(2,3\) 都满足时,需要都递归。注意每一层递归结束后需要 pushup 更新这一层的信息。
可以证明时间复杂度 \(O(\log n)\),具体怎么证我不会。
不论题目是什么要求,这一操作的方式是确定的,之后的线段树题目不会专门讲解这里。
void add(long long now,long long l,long long r,long long lc,long long rc,long long k)
{
pushdown(now);
if(l>=lc&&r<=rc)
{
tr[now].ad+=k,upd(now,k);
return;
}
long long mid=(l+r)>>1;
if(l<=mid)add(lc[now],l,mid,lc,rc,k);
if(r>=mid+1)add(rc[now],mid+1,r,lc,rc,k);
pushup(now);
}
在例题中有一些不同的码风,如果例题中的码风和这里讲述的码风都可取,我会在例题的讲解中标注出来。
权值线段树与动态开点
权值线段树
对于每个非叶节点 \([l,r]\),它的左儿子是 \([l,mid]\),右儿子是 \([mid+1,r]\),其中 \(mid=\lfloor\frac{l+r}{2}\rfloor\)。每个节点维护的是权值 \([l,r]\) 的信息。其余部分与正常线段树一样。
由于讲解较少,比较抽象,这里以维护权值 \([l,r]\) 中出现的元素数量为例。
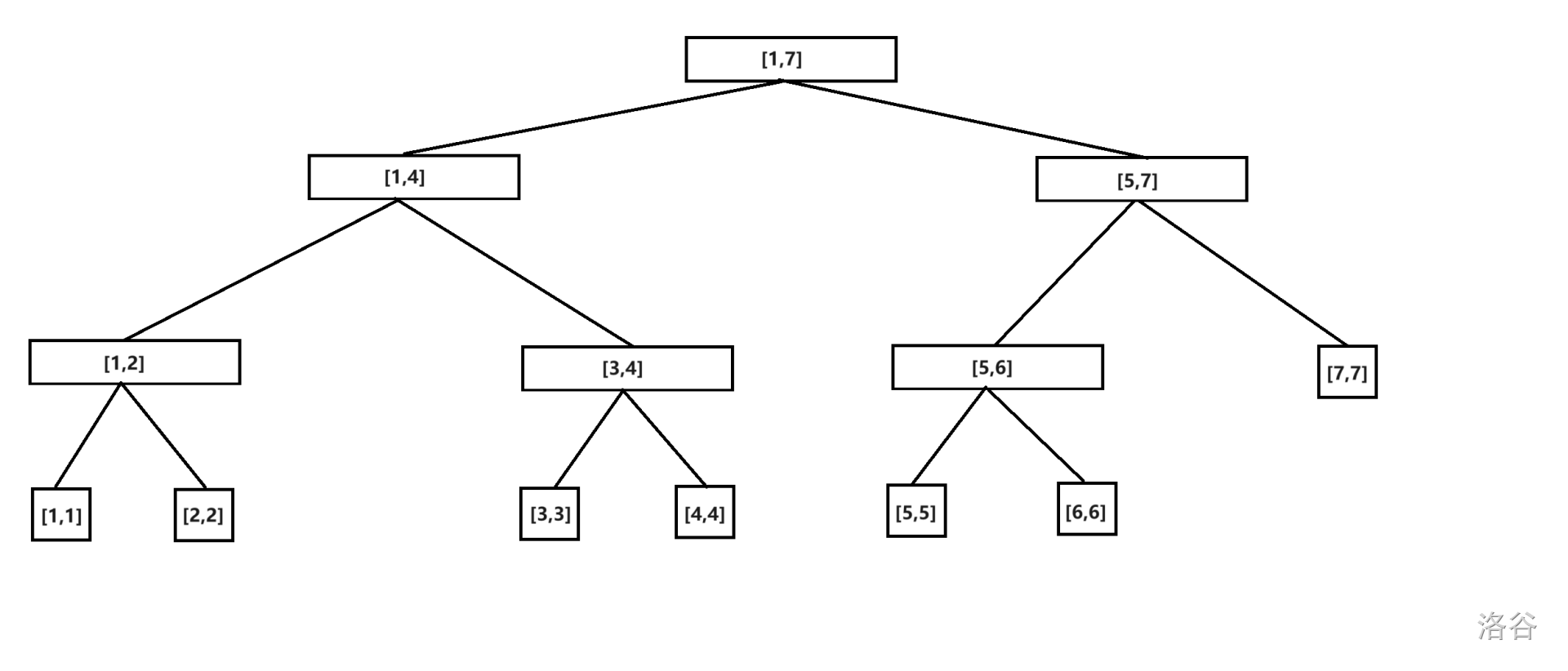
首先,先建立一棵线段树。

插入数字 \(4\)。节点旁边标红的数字是权值区间内的信息,也就是这个权值区间中出现了多少个元素。没有标注的默认为 \(0\)。
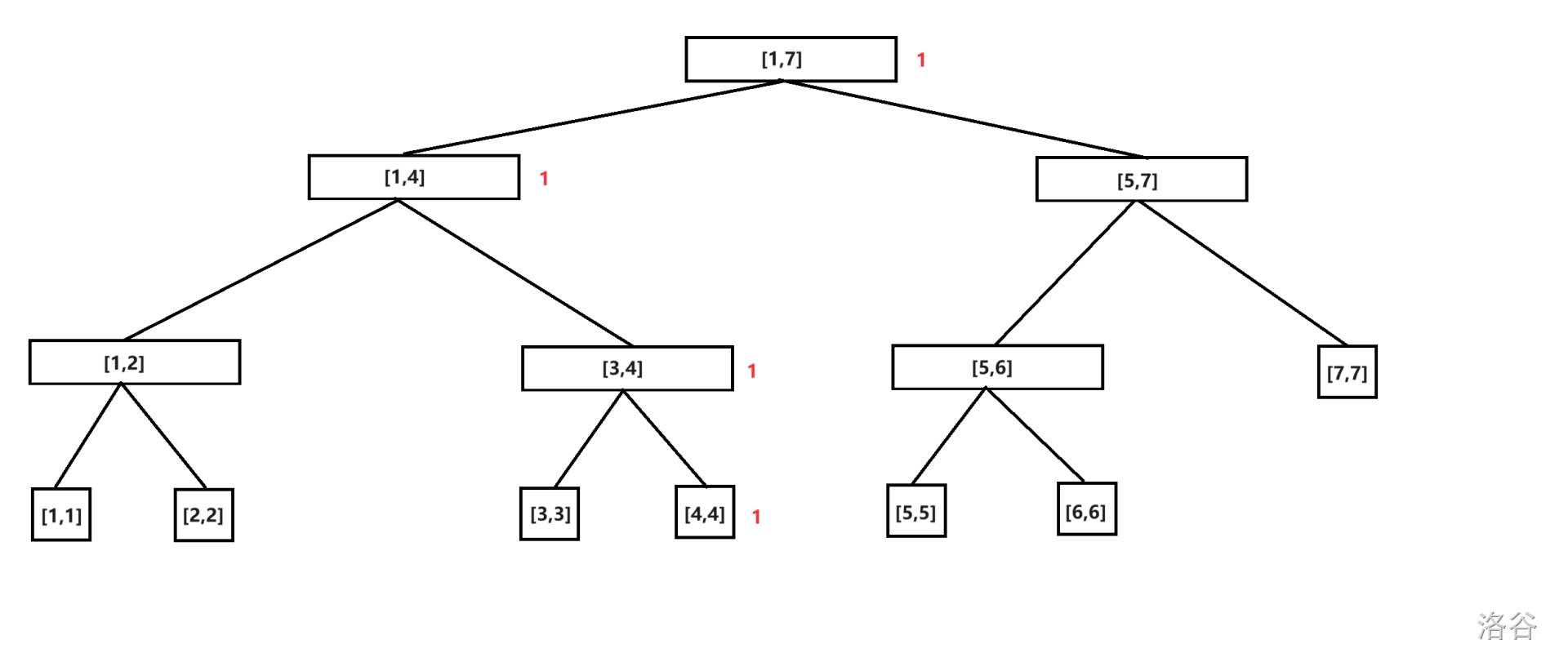
插入数字 \(7\)。
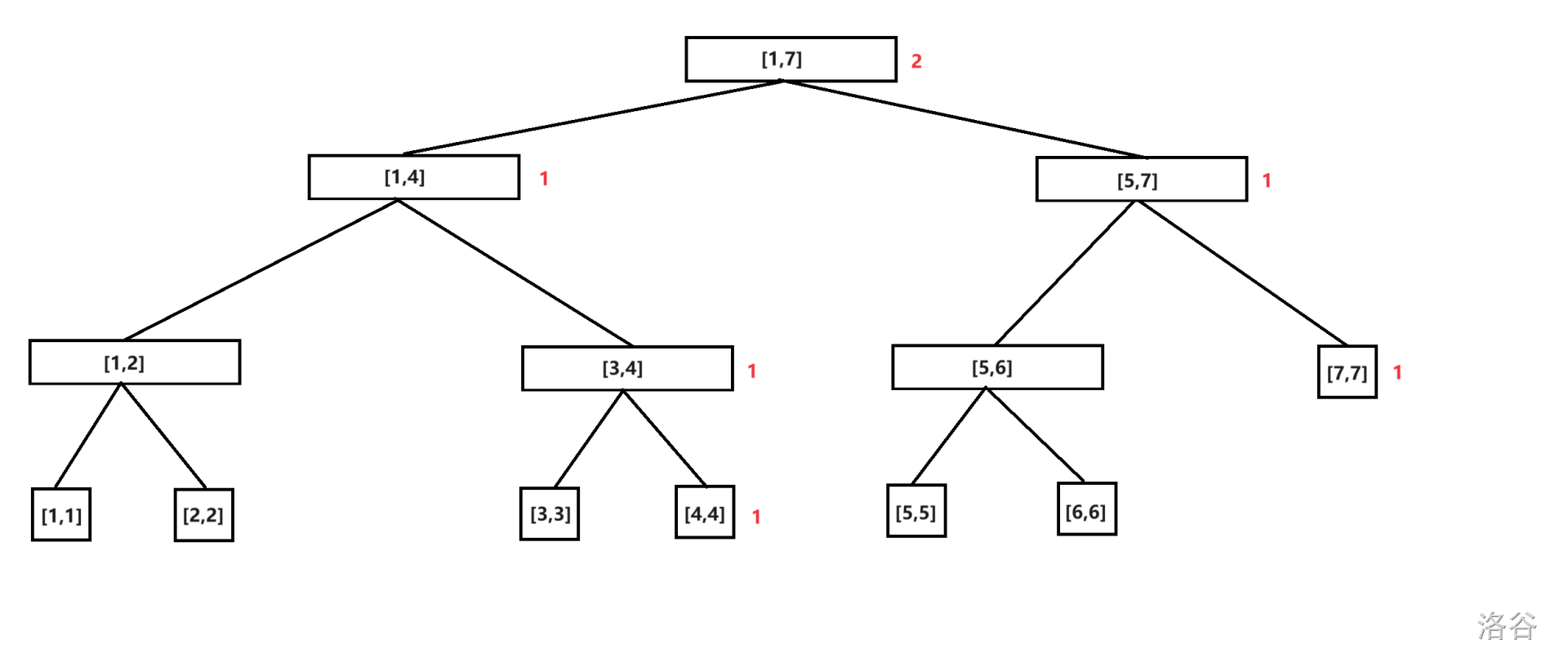
插入数字 \(5\)。
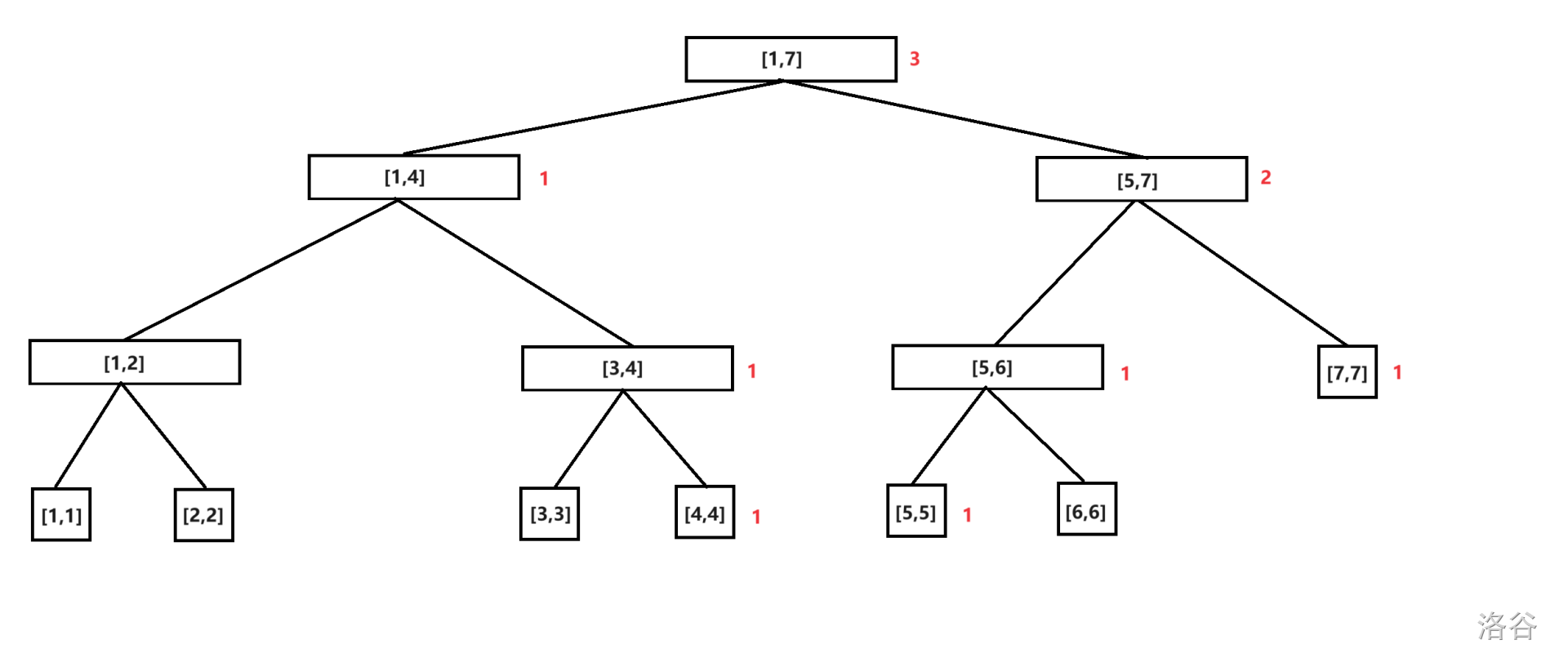
插入数字 \(6\)。
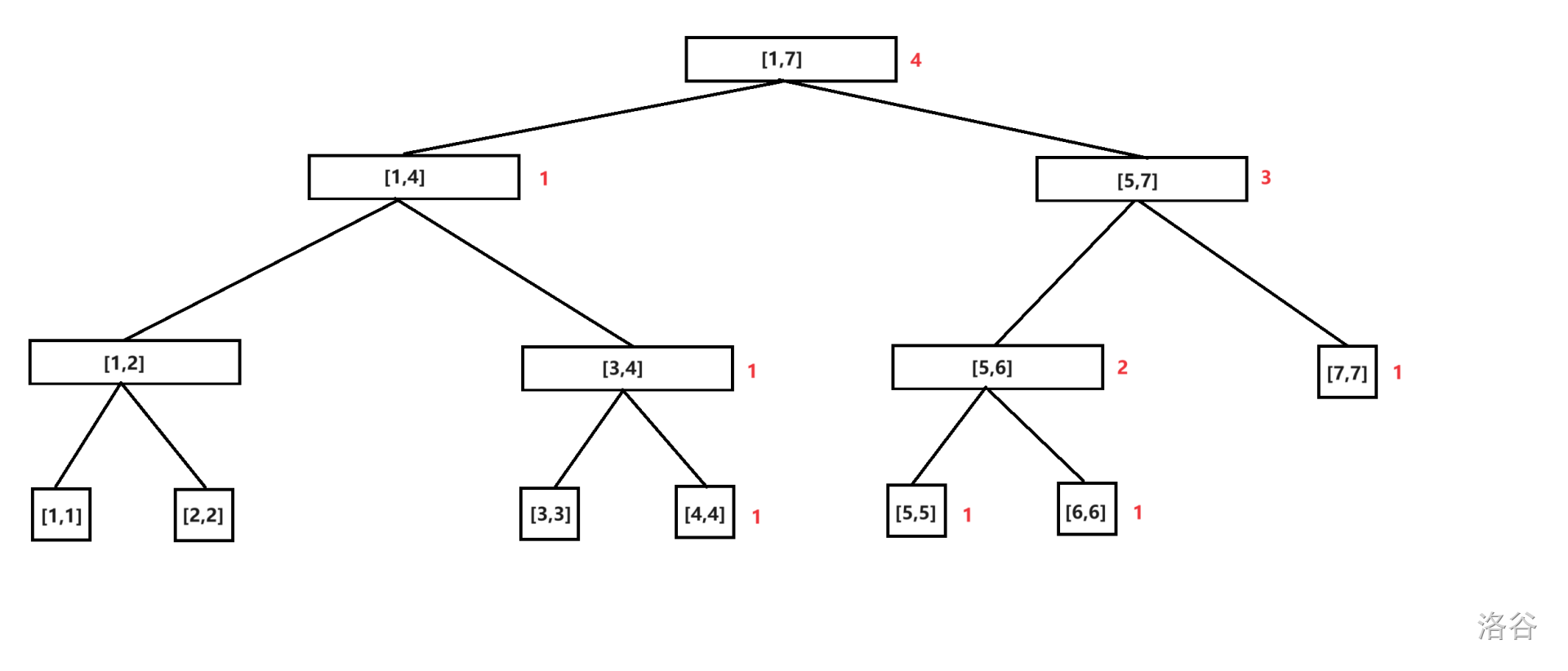
删除数字 \(5\)。
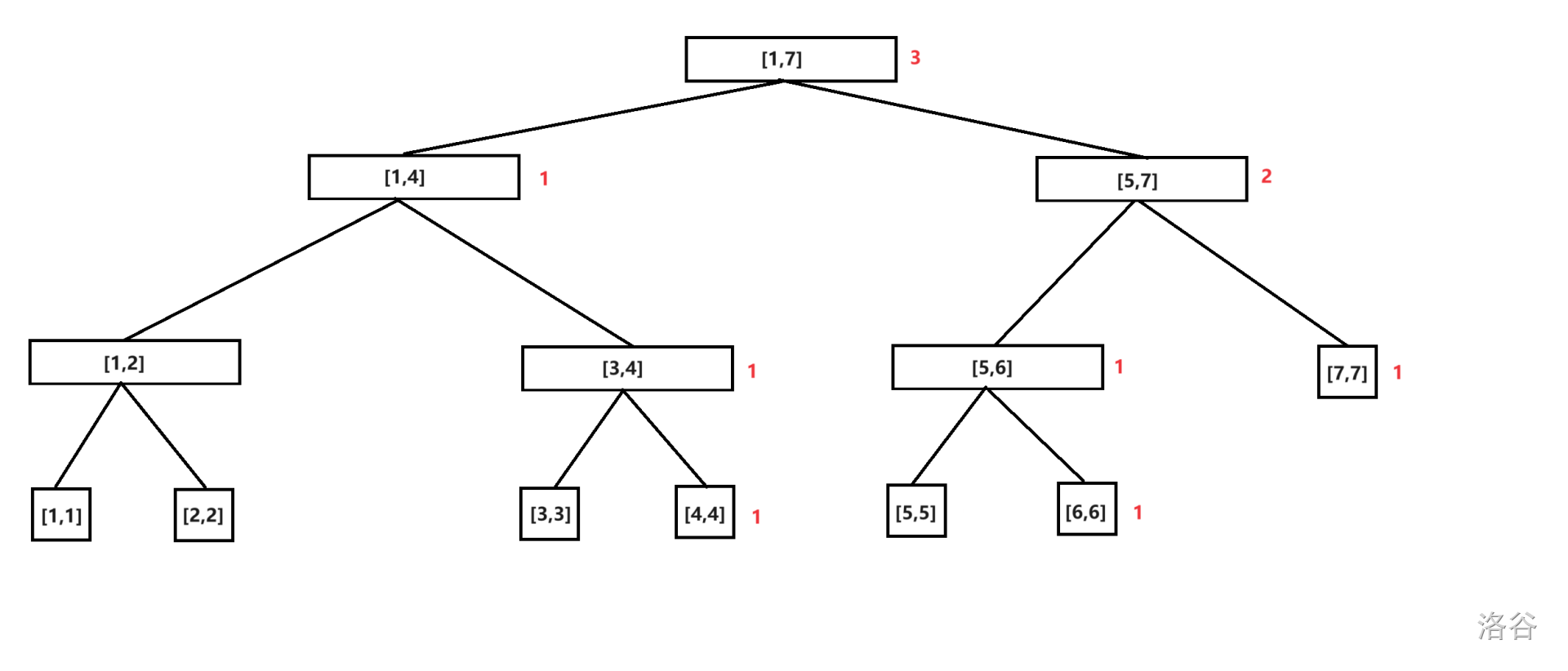
插入数字 \(6\)。
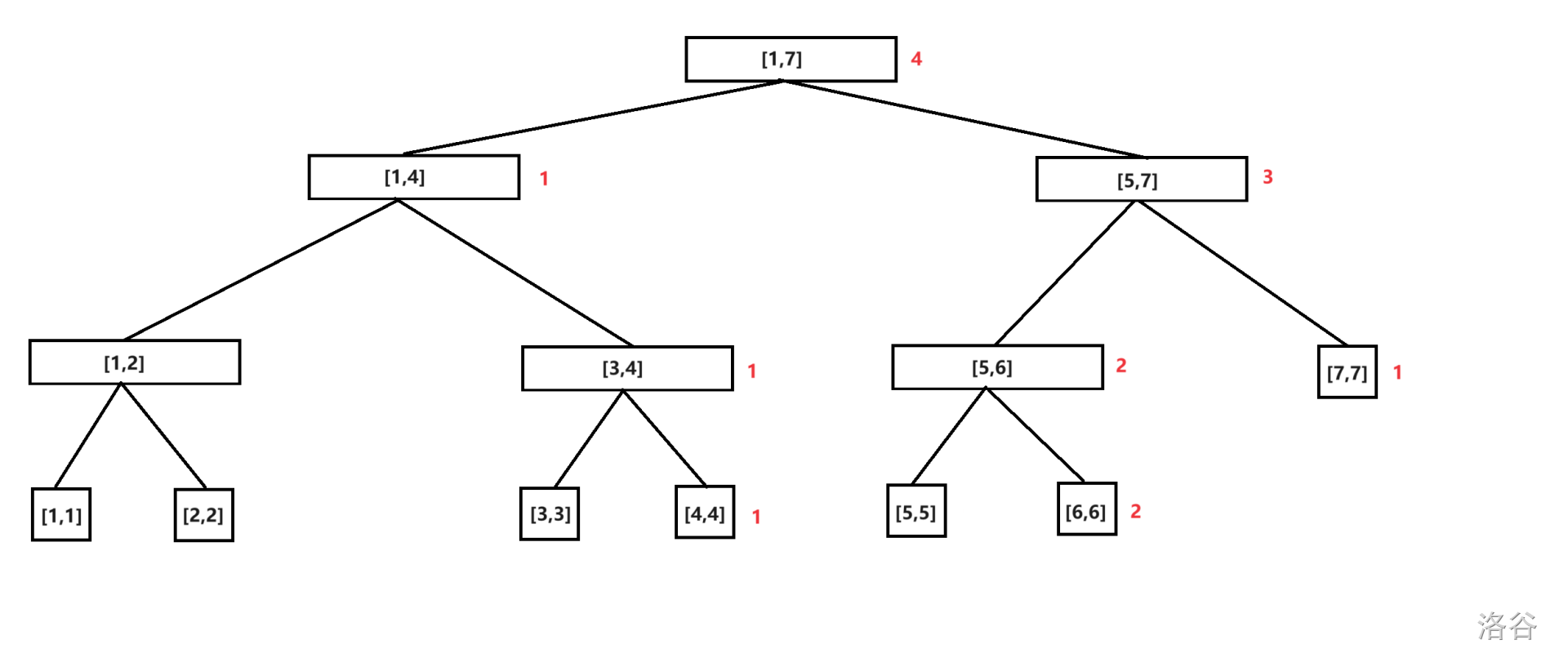
因为权值线段树可以维护一个集合中,一段权值区间中出现的元素数量,所以权值线段树可以在一定程度上代替平衡树。显然,权值线段树比平衡树好些得多。因此,我来举一个用权值线段树求集合第 \(k\) 小的例子。
假设现在的权值区间为 \([l,r]\),要查询当前区间第 \(k\) 小,节点 \(x\) 内的元素数量为 \(v[x]\) 有如下两种情况:
\(1\):\(k\le v[lc[x]]\),表示权值区间 \([l,mid]\) 中的数的数量大于等于 \(k\),那么第 \(k\) 小必然在 \([l,mid]\) 中,递归访问左儿子,查询第 \(k\) 小。
\(2\):\(k\gt v[lc[x]]\),表示权值区间 \([l,mid]\) 中的数的数量小于 \(k\),那么第 \(k\) 小必然在 \([mid+1,r]\) 中,递归访问右儿子,查询第 \(k-v[lc[x]]\) 小,因为有 \(v[lc[x]]\) 个数在左儿子中。
long long query(long long now,long long l,long long r,long long k)
{
pushdown(now);
if(l==r)return l;
long long mid=(l+r)>>1;
if(k<=tr[lc[now]].v)return query(lc[now],l,mid,,k);
else return query(rc[now],mid+1,r,k-tr[lc[now]].v);
}
动态开点
权值线段树有一个问题:如果权值范围是 \(1\sim10^9\),那就需要占用大量空间,以至于无法运行。因此,我们需要采用动态开点来降低空间的占用。
动态开点的思想是,只有一个节点被用到时,我们才给这个节点分配空间。所以,在修改时,我们访问到一个节点,如果这个节点为空,那么给这个节点分配空间。
以在权值线段树维护的集合中插入某个数为例,对权值线段树进行动态开点。
void insert(long long &now,long long l,long long r,long long k)
{
pushdown(now);
if(!now)now=++cnt;
if(l==r)
{
tr[now].v++;
return;
}
long long mid=(l+r)>>1;
if(k<=mid)insert(lc[now],l,mid,k);
else insert(rc[now],mid+1,r,k);
pushup(now);
}
设 \(c\) 为权值范围,\(m\) 为操作次数。使用动态开点后,每次操作至多新建 \(\log c\) 个节点,\(m\) 次操作至多建立 \(m\log c\) 个节点。当 \(m=10^5,c=2\times10^9\) 时,空间可以接受。所以,我们可以把动态开点权值线段树当作桶来用。
线段树合并
线段树合并算法可以用来合并两棵权值线段树,最常见的合并方式是将这两棵权值线段树维护的集合直接合并。
这相当于把两棵权值线段树各节点的权值相加。假设我们把树 \(x\) 合并到树 \(y\) 上,那么我们遍历 \(x,y\) 中每一个节点,在动态开点的情况下,有以下几种情况:
\(1\):如果 \(x,y\) 都有这个节点,那么把 \(x\) 合并到 \(y\) 上。
\(2\):只有 \(x\) 有这个节点,把 \(x\) 在 \(y\) 中对应的父亲节点对应 \(x\) 的儿子设为 \(x\)。通俗来讲,就是把 \(y\) 中的儿子指向 \(x\),便于利用已经有的,不变的信息,节约空间。
\(3\):只有 \(y\) 有这个节点,直接返回。
\(4\):如果 \(x,y\) 都没有这个节点,直接返回。
long long merge_tree(long long x,long long y)
{
if(!x)return y;
if(!y)return x;
tr[y].v=tr[x].v+tr[y].v;
lc[y]=merge_tree(lc[x],lc[y]);
rc[y]=merge_tree(rc[x],rc[y]);
return y;
}
线段树合并的时间复杂度为 \(O(m\log n)\),其中 \(m\) 为使用线段树合并时合并的总节点数。比如,合并一个节点数为 \(4\) 的树和节点数为 \(6\) 的树,\(m\) 就等于 \(10\)。
这里提供一个感性理解:根据线段树合并的过程,我们发现每进行一次合并,总结点数就会减少 \(1\),那么总结点数最多减少的次数与 \(m\) 同阶。再算上树形结构自带的 \(\log n\),时间复杂度就为 \(O(m\log n)\)。
线段树二分
假设我们需要从 \(l\) 开始向后找一个最近的对于某个值满足单调性的位置,使这个位置对应的这个值恰好为某个值。这种情况下一般可以先二分,然后用线段树判断,时间复杂度 \(O(\log^2 n)\)。
但是,通过线段树二分,我们可以做到 \(O(\log n)\)。而线段树二分也非常好写,只需要遍历线段树,然后把不满足判定条件的节点直接返回就行了。
这里判定条件既包含对应的这个值的判定条件,也包含线段树上区间必须与我二分的区间有交的判定条件。
这样复杂度是对的,因为满足要求的位置只有一个,所以只有 \(O(\log n)\) 个节点满足要求,而不满足要求的节点会被直接返回,所以时间复杂度为 \(O(\log n)\)。
其实线段树二分还能一次找出多个这种位置,相当于上面问题先找到了这个位置 \(l_1\),然后在同样的条件下找 \(l_2,l_3\dots\),线段树二分可以一次全部找到。因为上面是遍历线段树,所以如果我们可以判断多个位置时各个节点的合法情况,在找到一个位置后适当更新,就可以一次找齐。假设找了 \(k\) 个元素,则时间复杂度为 \(O(k\log n)\)。
举个例子,在序列某区间内上找若干个位置。我们可以维护线段树每个节点对应区间内有多少需要找的位置,然后遍历线段树,遇到没有要找的位置的节点或与查询的区间无交的节点直接返回。一直走到叶子节点,就是要找到位置,且均摊每个 \(O(\log n)\)。
void query(int x,int l,int r,int lx,int rx)
{
if(tr[x].cnt==0||l>rx||r<lx)return;
if(l==r)
{
findplace(l);
return;
}
int mid=(l+r)>>1;
query(lc(mid),l,mid,lx,rx),query(rc(mid),mid+1,r,lx,rx);
}
例题
例题 \(1\):
线段树模板题,不多赘述。
由于这一题历时较长,码风比较远古,但是底层逻辑和线段树讲解模块所述一样。现在的码风以线段树讲解模块为准。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long l,r,v,ad;
}tr[400000];
long long n,m,op,l,r,k,a[400000],root=1;
void pushup(long long now)
{
tr[now].v=tr[now*2].v+tr[now*2+1].v;
}
void pushdown(long long now)
{
long long k=tr[now].ad;
tr[now*2].ad+=k,tr[now*2].v+=k*(tr[now*2].r-tr[now*2].l+1);
tr[now*2+1].ad+=k,tr[now*2+1].v+=k*(tr[now*2+1].r-tr[now*2+1].l+1);
tr[now].ad=0;
}
void build(long long now,long long l,long long r)
{
tr[now].l=l,tr[now].r=r;
if(l==r)
{
tr[now].v=a[l];
return ;
}
build(now*2,l,(l+r)/2);build(now*2+1,(l+r)/2+1,r);
pushup(now);
}
void add(long long now,long long l,long long r,long long k)
{
if(l<=tr[now].l&&r>=tr[now].r)tr[now].ad+=k,tr[now].v+=k*(tr[now].r-tr[now].l+1);
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)add(now*2,l,r,k);
if(r>=mid+1)add(now*2+1,l,r,k);
pushup(now);
}
}
long long query(long long now,long long l,long long r)
{
long long ans=0;
if(l<=tr[now].l&&r>=tr[now].r)return tr[now].v;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)ans+=query(now*2,l,r);
if(r>=mid+1)ans+=query(now*2+1,l,r);
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
build(root,1,n);
for(long long i=1;i<=m;i++)
{
scanf("%lld",&op);
if(op==1)
{
scanf("%lld%lld%lld",&l,&r,&k);
add(root,l,r,k);
}
else if(op==2)
{
scanf("%lld%lld",&l,&r);
printf("%lld\n",query(root,l,r));
}
}
return 0;
}
例题 \(2\):
双倍经验
双懒标记的线段树,特别注意要维护好标记之间的关系。我们需要维护加法懒标记和乘法懒标记,对于多懒标记的线段树题目,我们可以人为规定优先级。我们发现先下传乘法标记方便维护一些,所有先下传乘法标记。
\(1\) 节点定义:区间和,加法标记,乘法标记。
\(2\) 上传/建树/区间查询/区间加:题目依旧是要维护区间和,与线段树 1 无异。
\(3\) 更新:加法标记的更新与线段树 1 相同,因为先下传乘法标记,后下传加法标记,加法标记对乘法标记没有影响。
乘法标记更新时,假设这个乘法标记为 \(k\),我们首先会发现,区间内每个数都乘以了 \(k\),整个区间的和也就乘以了 \(k\)。同时,由于先下传乘法标记,乘法标记对加法标记有影响。如果此时加法标记为 \(ad\),我们发现区间内每个数增加的部分也要乘以 \(k\),也就是说,加法标记 \(ad\) 也要乘以 \(k\)。
这里不需要增加整个区间的和,因为加法标记的影响在打加法标记的时候已经计算进了整个区间的和,整个区间的和也就乘以 \(k\) 已经包含了这一部分。
加法标记叠加时自然是两个标记相加,乘法标记叠加时自然是两个标记相乘。而当一个节点既下传加法标记,也下传乘法标记时,按照约定先下传乘法标记,处理影响,再下传加法标记,处理影响
由于这一题历时较长,码风比较远古,但是底层逻辑与上文一样。
P3373
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long l,r,v,ad,mu;
}tr[400000];
long long n,m,mod,op,l,r,k,a[400000],root=1;
void pushup(long long now)
{
tr[now].v=(tr[now*2].v+tr[now*2+1].v)%mod;
}
void pushdown(long long now)
{
long long k1=tr[now].ad,k2=tr[now].mu;
tr[now*2].v=(tr[now*2].v*k2%mod+k1*(tr[now*2].r-tr[now*2].l+1))%mod;
tr[now*2+1].v=(tr[now*2+1].v*k2%mod+k1*(tr[now*2+1].r-tr[now*2+1].l+1))%mod;
tr[now*2].ad=(tr[now*2].ad*k2+k1)%mod;
tr[now*2+1].ad=(tr[now*2+1].ad*k2+k1)%mod;
tr[now*2].mu=tr[now*2].mu*k2%mod;
tr[now*2+1].mu=tr[now*2+1].mu*k2%mod;
tr[now].ad=0;tr[now].mu=1;
}
void build(long long now,long long l,long long r)
{
tr[now].l=l,tr[now].r=r,tr[now].mu=1;
if(l==r)
{
tr[now].v=a[l];
return ;
}
build(now*2,l,(l+r)/2);build(now*2+1,(l+r)/2+1,r);
pushup(now);
}
void add(long long now,long long l,long long r,long long k)
{
if(l<=tr[now].l&&r>=tr[now].r)tr[now].ad+=k,tr[now].v+=k*(tr[now].r-tr[now].l+1),tr[now].ad%=mod,tr[now].v%=mod;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)add(now*2,l,r,k);
if(r>=mid+1)add(now*2+1,l,r,k);
pushup(now);
}
}
void mul(long long now,long long l,long long r,long long k)
{
if(l<=tr[now].l&&r>=tr[now].r)tr[now].mu*=k,tr[now].v*=k,tr[now].ad*=k,tr[now].mu%=mod,tr[now].v%=mod,tr[now].ad%=mod;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)mul(now*2,l,r,k);
if(r>=mid+1)mul(now*2+1,l,r,k);
pushup(now);
}
}
long long query(long long now,long long l,long long r)
{
long long ans=0;
if(l<=tr[now].l&&r>=tr[now].r)return tr[now].v;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)ans+=query(now*2,l,r);
if(r>=mid+1)ans+=query(now*2+1,l,r);
ans%=mod;
}
return ans;
}
int main()
{
scanf("%lld%lld%lld",&n,&m,&mod);
for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
build(root,1,n);
for(long long i=1;i<=m;i++)
{
scanf("%lld",&op);
if(op==1)
{
scanf("%lld%lld%lld",&l,&r,&k);
mul(root,l,r,k);
}
else if(op==2)
{
scanf("%lld%lld%lld",&l,&r,&k);
add(root,l,r,k);
}
else if(op==3)
{
scanf("%lld%lld",&l,&r);
printf("%lld\n",query(root,l,r));
}
}
return 0;
}
P2023
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long l,r,v,ad,mu;
}tr[400000];
long long n,m,mod,op,l,r,k,a[400000],root=1;
void pushup(long long now)
{
tr[now].v=(tr[now*2].v+tr[now*2+1].v)%mod;
}
void pushdown(long long now)
{
long long k1=tr[now].ad,k2=tr[now].mu;
tr[now*2].v=(tr[now*2].v*k2%mod+k1*(tr[now*2].r-tr[now*2].l+1))%mod;
tr[now*2+1].v=(tr[now*2+1].v*k2%mod+k1*(tr[now*2+1].r-tr[now*2+1].l+1))%mod;
tr[now*2].ad=(tr[now*2].ad*k2+k1)%mod;
tr[now*2+1].ad=(tr[now*2+1].ad*k2+k1)%mod;
tr[now*2].mu=tr[now*2].mu*k2%mod;
tr[now*2+1].mu=tr[now*2+1].mu*k2%mod;
tr[now].ad=0;tr[now].mu=1;
}
void build(long long now,long long l,long long r)
{
tr[now].l=l,tr[now].r=r,tr[now].mu=1;
if(l==r)
{
tr[now].v=a[l];
return ;
}
build(now*2,l,(l+r)/2);build(now*2+1,(l+r)/2+1,r);
pushup(now);
}
void add(long long now,long long l,long long r,long long k)
{
if(l<=tr[now].l&&r>=tr[now].r)tr[now].ad+=k,tr[now].v+=k*(tr[now].r-tr[now].l+1),tr[now].ad%=mod,tr[now].v%=mod;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)add(now*2,l,r,k);
if(r>=mid+1)add(now*2+1,l,r,k);
pushup(now);
}
}
void mul(long long now,long long l,long long r,long long k)
{
if(l<=tr[now].l&&r>=tr[now].r)tr[now].mu*=k,tr[now].v*=k,tr[now].ad*=k,tr[now].mu%=mod,tr[now].v%=mod,tr[now].ad%=mod;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)mul(now*2,l,r,k);
if(r>=mid+1)mul(now*2+1,l,r,k);
pushup(now);
}
}
long long query(long long now,long long l,long long r)
{
long long ans=0;
if(l<=tr[now].l&&r>=tr[now].r)return tr[now].v;
else
{
long long mid=(tr[now].l+tr[now].r)/2;
pushdown(now);
if(l<=mid)ans+=query(now*2,l,r);
if(r>=mid+1)ans+=query(now*2+1,l,r);
ans%=mod;
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&mod);
for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
scanf("%lld",&m);
build(root,1,n);
for(long long i=1;i<=m;i++)
{
scanf("%lld",&op);
if(op==1)
{
scanf("%lld%lld%lld",&l,&r,&k);
mul(root,l,r,k);
}
else if(op==2)
{
scanf("%lld%lld%lld",&l,&r,&k);
add(root,l,r,k);
}
else if(op==3)
{
scanf("%lld%lld",&l,&r);
printf("%lld\n",query(root,l,r));
}
}
return 0;
}
例题 \(3\):
平均数不需要专门维护,维护区间和后直接用维护区间和除以区间长度即可。
对于方差,我们展开方差的定义式:
我们可以直接算出平均数 \(\overline A\),并通过过线段树维护 \(\sum\limits_{i=1}^nA_i\),也就是区间和以及 \(\sum\limits_{i=1}^nA_i^2\),也就是区间平方和。维护这些东西之后,代入式子就可以求出方差。
\(1\) 节点定义:区间和,区间平方和,加法标记。
\(2\) 上传:区间和,区间平方和均可以由左右儿子的区间和,区间平方和相加得到。
\(3\) 建树:区间 \([x,x]\) 的区间和为 \(x\),区间平方和为 \(x^2\)。
\(4\) 区间查询:分两种,查询区间和与查询区间平方和。与线段树 1 中的区间查询基本相同,把查询返回的值对应改成区间和或查询区间平方和即可。
\(5\) 区间加:与线段树 1 中的区间查询相同。
\(6\) 更新:对于区间和的更新,与线段树 1 中的区间查询相同。
对于区间平方和的更新,我们又需要推一下式子。设序列范围为 \([l,r]\),修改前序列为 \(A\),修改后序列为 \(A'\),修改时增加 \(k\)。
我们发现 \(\sum_{i=l}^rA_i^2\) 就是修改前区间平方和,\(\sum_{i=l}^rA_i\) 就是修改前区间和,所以修改后的区间平方和可以直接求出。注意由于这里用到的是修改前区间和,所以要先更新区间平方和,再更新区间和。
#include <bits/stdc++.h>
using namespace std;
struct node
{
double l,r,v,vs,ad;
}tr[800000];
long long n,m,op,x,y,lc[800000],rc[800000],cnt=0,root=1;
double k,a[800000];
void upd(long long x,double k)
{
tr[x].vs+=k*k*(tr[x].r-tr[x].l+1)+2*tr[x].v*k;
tr[x].v+=k*(tr[x].r-tr[x].l+1);
}
void pushup(long long x)
{
tr[x].v=tr[lc[x]].v+tr[rc[x]].v;
tr[x].vs=tr[lc[x]].vs+tr[rc[x]].vs;
}
void pushdown(long long x)
{
tr[lc[x]].ad+=tr[x].ad,tr[rc[x]].ad+=tr[x].ad;
if(lc[x])upd(lc[x],tr[x].ad);
if(rc[x])upd(rc[x],tr[x].ad);
tr[x].ad=0;
}
void build(long long now,long long l,long long r)
{
tr[now].l=l,tr[now].r=r;
if(l==r)
{
tr[now].v=a[l],tr[now].vs=a[l]*a[l];
return;
}
lc[now]=now*2,rc[now]=now*2+1;
long long mid=(l+r)/2;
build(lc[now],l,mid),build(rc[now],mid+1,r);
pushup(now);
}
void add(long long now,long long l,long long r,double k)
{
pushdown(now);
if(tr[now].l>=l&&tr[now].r<=r)
{
tr[now].ad+=k,upd(now,k);
return;
}
long long mid=(tr[now].l+tr[now].r)/2;
if(l<=mid)add(lc[now],l,r,k);
if(r>=mid+1)add(rc[now],l,r,k);
pushup(now);
}
double query(long long now,long long l,long long r)
{
pushdown(now);
double ans=0;
if(tr[now].l>=l&&tr[now].r<=r)return tr[now].v;
long long mid=(tr[now].l+tr[now].r)/2;
if(l<=mid)ans+=query(lc[now],l,r);
if(r>=mid+1)ans+=query(rc[now],l,r);
return ans;
}
double querys(long long now,long long l,long long r)
{
pushdown(now);
double ans=0;
if(tr[now].l>=l&&tr[now].r<=r)return tr[now].vs;
long long mid=(tr[now].l+tr[now].r)/2;
if(l<=mid)ans+=querys(lc[now],l,r);
if(r>=mid+1)ans+=querys(rc[now],l,r);
return ans;
}
void update()
{
scanf("%lld%lld%lf",&x,&y,&k);
add(root,x,y,k);
}
double average()
{
scanf("%lld%lld",&x,&y);
return query(root,x,y)/(y-x+1);
}
double variance()
{
scanf("%lld%lld",&x,&y);
double ave=query(root,x,y)/(y-x+1);
return ave*ave+(querys(root,x,y)-2*query(root,x,y)*ave)/(y-x+1);
}
int main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)scanf("%lf",&a[i]);
build(root,1,n);
for(int i=1;i<=m;i++)
{
scanf("%lld",&op);
if(op==1)update();
else if(op==2)printf("%.4lf\n",average());
else if(op==3)printf("%.4lf\n",variance());
}
return 0;
}
这一份代码采取了不同的写法,线段树知识点讲解和这里的两种写法都可以。
这份代码把线段树每个节点代表区间的 \(l,r\) 预处理出来,这样在查询/修改函数中就不需要单独开两个变量记录 \(l,r\) 了。这样做的缺点是会占用一定的空间,有的空间卡得紧的题目会被卡常。
例题 \(4\):
经典的线段树例题,做完这题对线段树的理解会深入很多。
题目要求最大子段和,所以在线段树中我们也需要维护最大子段和。
最大子段和不能直接维护,所以我们维护一些别的东西来求出最大子段和。一个区间 \([l,r]\) 的最大子段和可以直接从 \([l,mid]\) 或 \([mid+1,r]\) 继承,也可以由 \([l,mid]\) 的最右边的一部分与 \([mid+1,r]\) 最左边的一部分合并得到。所以,我们需要维护每个区间的最大前缀和和最大后缀和,用于合并得出最大子段和。
最大前缀和和最大后缀和也不能直接维护,所以我们又要维护一些别的东西来求出最大前缀和和最大后缀和。一个区间 \([l,r]\) 的最大前缀和可以直接从 \([l,mid]\) 继承,也可以由 \([l,mid]\) 的最右边的一部分与 \([mid+1,r]\) 的区间和合并得到。一个区间 \([l,r]\) 的最大后缀和可以直接从 \([mid+1,r]\) 继承,也可以由 \([mid+1,r]\) 的最左边的一部分与 \([l,mid]\) 的区间和合并得到。所以,我们还需要维护每个区间的区间和。
由于这题是单点修改,所以不需要懒标记。每次修改完了之后,我们使用 pushup 更新一下访问过的节点即可。
\(1\) 节点定义:区间和,最大前缀和,最大后缀和,最大子段和。
\(2\) 上传:依据上文所说,合并两个区间的各项元素即可。注意不能与空节点合并,代码中一些赋值为无穷的操作就是为了避免与空节点合并。
\(3\) 建树:区间 \([x,x]\) 的区间和为 \(x\),最大前缀和为 \(x\),最大后缀和为 \(x\),最大子段和为 \(x\)。(废话)
\(4\) 区间查询:在线段树上递归,将原查询区间划分为若干个子区间。从左到右按照上传的方式合并每个区间,在最后合并的总区间中查询最大字段和。线段树 1 中查询时合并区间就是从左到右的顺序,因为先访问左儿子,再访问右儿子。因为需要完整合并区间,这次需要返回一个 node 结构体。
\(5\) 单点修改:依据上文所说,记得更新访问到的节点。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long l,r,v,s,rm,lm;
}tr[6000000];
long long n,m,op,p,l,r,k,lc[6000000],rc[6000000],a[6000000],root=1;
long long const INF=99999999;
void pushup(long long now)
{
tr[now].v=tr[lc[now]].v+tr[rc[now]].v;
tr[now].lm=max(tr[lc[now]].lm,tr[lc[now]].v+tr[rc[now]].lm);
tr[now].rm=max(tr[rc[now]].rm,tr[rc[now]].v+tr[lc[now]].rm);
tr[now].s=max(max(tr[lc[now]].s,tr[rc[now]].s),tr[lc[now]].rm+tr[rc[now]].lm);
}
void build(long long now,long long l,long long r)
{
tr[now].l=l,tr[now].r=r,lc[now]=now*2,rc[now]=now*2+1;
if(l==r)
{
tr[now].v=a[l],tr[now].lm=a[l],tr[now].rm=a[l],tr[now].s=a[l];
tr[lc[now]].v=0,tr[lc[now]].lm=-INF,tr[lc[now]].rm=-INF,tr[lc[now]].s=-INF;
tr[rc[now]].v=0,tr[rc[now]].lm=-INF,tr[rc[now]].rm=-INF,tr[rc[now]].s=-INF;
return;
}
build(lc[now],l,(l+r)/2);build(rc[now],(l+r)/2+1,r);
pushup(now);
}
void update(long long now,long long p,long long k)
{
if(tr[now].l==p&&tr[now].r==p)
{
tr[now].v=k,tr[now].lm=k,tr[now].rm=k,tr[now].s=k;
return;
}
else
{
long long mid=(tr[now].l+tr[now].r)/2;
if(p<=mid)update(lc[now],p,k);
if(p>=mid+1)update(rc[now],p,k);
pushup(now);
}
}
struct node query(long long now,long long l,long long r)
{
struct node ans;
if(l<=tr[now].l&&r>=tr[now].r)return tr[now];
else
{
long long mid=(tr[now].l+tr[now].r)/2;
if(r<=mid)return query(lc[now],l,r);
if(l>=mid+1)return query(rc[now],l,r);
}
struct node lh=query(lc[now],l,r),rh=query(rc[now],l,r);
ans.v=lh.v+rh.v;
ans.lm=max(lh.lm,lh.v+rh.lm);
ans.rm=max(rh.rm,rh.v+lh.rm);
ans.s=max(max(lh.s,rh.s),lh.rm+rh.lm);
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
build(root,1,n);
for(long long i=1;i<=m;i++)
{
scanf("%lld",&op);
if(op==1)
{
scanf("%lld%lld",&l,&r);
if(l>r)swap(l,r);
printf("%lld\n",query(root,l,r).s);
}
else if(op==2)
{
scanf("%lld%lld",&p,&k);
update(root,p,k);
}
}
return 0;
}
这一份代码采取了不同的写法,线段树知识点讲解和这里的两种写法都可以。
这里的查询函数中对于情况的判定使用了另一种方法。
\(1\):\(lc\le l,rc\ge r\),直接返回这个区间维护的信息,因为 \([l,r]\) 被完整包含在查询区间中,区间内所有的元素都会被统计,直接返回维护的信息。
\(2\):\(rc\le mid\),递归访问左儿子 \([l,mid]\),因为整个查询区间被完整包含在 \([l,mid]\) 中。
\(3\):\(lc\ge mid+1\),递归访问右儿子 \([mid+1,r]\),因为整个查询区间被完整包含在 \([mid+1,r]\) 中。
\(4\):其他情况。整个区间既不被完整包含在 \([l,mid]\) 中,也不被完整包含在 \([mid+1,r]\) 中。那么,递归访问左儿子 \([l,mid]\) 和右儿子 \([mid+1,r]\),因为查询区间有一部分在 \([l,mid]\) 中,有一部分在 \([mid+1,r]\) 中。
这样做的好处是方便合并,具体方便之处可以看代码。
例题 \(5\):
由于有查询第 \(k\) 大的操作,我们考虑使用权值线段树。由于权值范围比较大,我们使用动态开点权值线段树。
对于整体增加/减少操作,我们维护一个偏移量 \(ad\)。每次减少操作之后,需要删除所有小于 \(\min+ad\) 的元素并计入答案。具体可以在线段树中递归,以区间修改的方式将区间 \([1,\min+ad-1]\) 全部赋值为 \(0\)。并设立一个清零懒标记,更新方式是将当前节点的权值清 \(0\)。
对于插入操作,我们插入的值需要减少偏移量,因为这个值不受之前的偏移量影响,为了适配整个集合的偏移量,必须要减少偏移量。因此,插入的数可能为负数。
对于查询第 \(k\) 大的操作,我们使用类似查询第 \(k\) 小的方法,在线段树中递归。
假设现在的权值区间为 \([l,r]\),要查询当前区间第 \(k\) 大,节点 \(x\) 内的元素数量为 \(v[x]\) 有如下两种情况:
\(1\):\(k\le v[rc[x]]\),表示权值区间 \([mid+1,r]\) 中的数的数量大于等于 \(k\),那么第 \(k\) 大必然在 \([mid+1,r]\) 中,递归访问右儿子,查询第 \(k\) 大。
\(2\):\(k\gt v[rc[x]]\),表示权值区间 \([mid+1,r]\) 中的数的数量小于 \(k\),那么第 \(k\) 小必然在 \([l,mid]\) 中,递归访问左儿子,查询第 \(k-v[rc[x]]\) 小,因为有 \(v[rc[x]]\) 个数在右儿子中。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long v,cl;
}tr[4000000];
long long n,mi,ad,x,root,lc[4000000],rc[4000000],cnt,ans=0;
char op;
void pushup(long long x)
{
tr[x].v=tr[lc[x]].v+tr[rc[x]].v;
}
void pushdown(long long x)
{
if(tr[x].cl==1)
{
tr[lc[x]].cl=1,tr[lc[x]].v=0;
tr[rc[x]].cl=1,tr[rc[x]].v=0;
tr[x].cl=0;
}
}
void insert(long long &now,long long l,long long r,long long k)
{
pushdown(now);
if(!now)now=++cnt;
if(l==r)
{
tr[now].v++;
return;
}
long long mid=(l+r)>>1;
if(k<=mid)insert(lc[now],l,mid,k);
else insert(rc[now],mid+1,r,k);
pushup(now);
}
void del(long long now,long long l,long long r,long long k)
{
if(!now)return;
pushdown(now);
if(l==r)
{
if(l<=k)ans+=tr[now].v,tr[now].v=0;
return;
}
long long mid=(l+r)>>1;
if(k>=mid+1)tr[lc[now]].cl=1,ans+=tr[lc[now]].v,tr[lc[now]].v=0,del(rc[now],mid+1,r,k);
else if(k>=l)del(lc[now],l,mid,k);
pushup(now);
}
long long ranks(long long now,long long l,long long r,long long k)
{
if(l==r)return l;
pushdown(now);
long long mid=(l+r)>>1;
if(k>tr[rc[now]].v)return ranks(lc[now],l,mid,k-tr[rc[now]].v);
else if(k<=tr[rc[now]].v)return ranks(rc[now],mid+1,r,k);
pushup(now);
}
int main()
{
cin>>n>>mi;
for(int i=1;i<=n;i++)
{
cin>>op>>x;
if(op=='I')
{
if(x<mi)continue;
insert(root,-2e5,2e5,x-ad);
}
else if(op=='A')ad+=x;
else if(op=='S')
{
ad-=x;
del(root,-2e5,2e5,mi-ad-1);
}
else if(op=='F')
{
if(x>tr[root].v)
{
printf("-1\n");
continue;
}
printf("%lld\n",ranks(root,-2e5,2e5,x)+ad);
}
}
printf("%lld\n",ans);
return 0;
}
例题 \(6\):
由于有合并操作,考虑使用并查集。由于有查询第 \(k\) 小操作,考虑对于每一个集合开一个权值线段树,维护权值范围内出现的数的数量。这样,我们就可以对于每个集合查询第 \(k\) 小了。
两个集合合并时,两个集合的权值线段树也要合并。然后就是线段树合并模板了,不多赘述。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long v;
}tr[2000000];
long long n,m,p,u,v,q,a[2000000],y[2000000],f[2000000],rt[2000000],lc[2000000],rc[2000000],cnt=0;
char op;
long long getf(long long x)
{
if(f[x]==x)return x;
else return f[x]=getf(f[x]);
}
long long merge_tree(long long x,long long y)
{
if(!x)return y;
if(!y)return x;
tr[y].v=tr[x].v+tr[y].v;
lc[y]=merge_tree(lc[x],lc[y]);
rc[y]=merge_tree(rc[x],rc[y]);
return y;
}
void merge(long long x,long long y)
{
long long p=getf(x),q=getf(y);
if(p==q)return;
f[p]=q;
rt[q]=merge_tree(rt[p],rt[q]);
}
void pushup(long long x)
{
tr[x].v=tr[lc[x]].v+tr[rc[x]].v;
}
void insert(long long &now,long long l,long long r,long long k)
{
if(!now)now=++cnt;
if(l==r)
{
tr[now].v++;
return;
}
long long mid=(l+r)>>1;
if(k<=mid)insert(lc[now],l,mid,k);
else insert(rc[now],mid+1,r,k);
pushup(now);
}
long long query(long long now,long long l,long long r,long long k)
{
if(l==r)return l;
long long mid=(l+r)>>1;
if(k>tr[lc[now]].v)return query(rc[now],mid+1,r,k-tr[lc[now]].v);
else return query(lc[now],l,mid,k);
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
f[i]=i,y[a[i]]=i,insert(rt[i],1,n,a[i]);
}
for(int i=1;i<=m;i++)
{
cin>>u>>v;
merge(u,v);
}
cin>>q;
for(int i=1;i<=q;i++)
{
cin>>op>>u>>v;
if(op=='B')merge(u,v);
else if(op=='Q')
{
long long z=getf(u);
if(tr[rt[z]].v<v)printf("-1\n");
else printf("%lld\n",y[query(rt[z],1,n,v)]);
}
}
return 0;
}
例题 \(7\):
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
一点也不模板。
树上路径修改,查询只有最终一次,考虑树上差分。由于救济粮有很多种类型,所以我们需要开桶来存储每一种救济粮的差分值。然而,每个节点开一个桶空间肯定不够,所以我们需要使用权值线段树来代替桶。自然,本来两个桶的合并就变成了线段树合并。
我们需要在这个权值线段树中维护最大值,我们只需要记录最大值的出现次数和最大值的值。当我们合并两个区间时,把第二个区间的最大值出现次数与第一个区间的最大值出现次数比较,不相等取大的,相等取最大值的值较小的。
需要注意的是,每一次合并完一个点后就立即计算答案,因为以后的合并可能会影响这个答案。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,nxt;
}e[400000];
struct node
{
int v,mx;
}tr[40000000];
int n,m,x,y,z,ans[400000],rt[400000],lc[40000000],rc[40000000],h[400000],dep[400000],fa[400000][40],ce=0,cnt=0;
void add_edge(int u,int v)
{
e[++ce].nxt=h[u];
e[ce].v=v;
h[u]=ce;
}
void dfs1(int now,int f)
{
fa[now][0]=f,dep[now]=dep[f]+1;
for(int i=1;i<=30;i++)
if(fa[fa[now][i-1]][i-1]!=0)fa[now][i]=fa[fa[now][i-1]][i-1];
else break;
for(int i=h[now];i;i=e[i].nxt)
if(e[i].v!=f)dfs1(e[i].v,now);
}
int lca(int x,int y)
{
if(dep[x]>dep[y])swap(x,y);
int c=dep[y]-dep[x];
for(int i=30;i>=0;i--)
if((1<<i)&c)y=fa[y][i];
if(x==y)return x;
for(int i=30;i>=0;i--)
if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
void pushup(int x)
{
tr[x].mx=0,tr[x].v=-99999999;
if(tr[lc[x]].v!=0)tr[x].mx=tr[lc[x]].mx,tr[x].v=tr[lc[x]].v;
if(tr[rc[x]].v!=0&&(tr[rc[x]].v>tr[x].v))tr[x].mx=tr[rc[x]].mx,tr[x].v=tr[rc[x]].v;
}
void insert(int &now,int l,int r,int k,int c)
{
if(!now)now=++cnt;
if(l==r)
{
tr[now].v+=c,tr[now].mx=l;
return;
}
int mid=(l+r)>>1;
if(k<=mid)insert(lc[now],l,mid,k,c);
else insert(rc[now],mid+1,r,k,c);
pushup(now);
}
void merge(int x,int &y,int l,int r)
{
if(!x)return;
if(!y)
{
y=x;
return;
}
if(l==r)
{
tr[y].v+=tr[x].v,tr[y].mx=l;
return;
}
int mid=(l+r)>>1;
merge(lc[x],lc[y],l,mid);
merge(rc[x],rc[y],mid+1,r);
pushup(y);
}
void dfs2(int now,int f)
{
for(int i=h[now];i;i=e[i].nxt)
if(e[i].v!=f)
{
dfs2(e[i].v,now);
merge(rt[e[i].v],rt[now],1,1e5);
}
ans[now]=tr[rt[now]].mx;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&x,&y);
add_edge(x,y),add_edge(y,x);
}
dfs1(1,0);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
int l=lca(x,y);
insert(rt[x],1,1e5,z,1);
insert(rt[y],1,1e5,z,1);
insert(rt[l],1,1e5,z,-1);
if(fa[l][0]!=0)insert(rt[fa[l][0]],1,1e5,z,-1);
}
dfs2(1,0);
for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
return 0;
}
这一份代码采取了不同的写法,线段树合并知识点讲解和这里的两种写法都可以。比较推荐这一种写法。
这一种写法使用了引用,于是 merge 函数就不需要有返回值了。
在这个写法中,在访问到某个节点不着急更新,而是一直递归到叶节点,更新叶节点之后通过 pushup 来更新每个节点。由于叶节点比较好更新,这种写法可以大大降低一些上传比较复杂的题目的代码实现难度,降低错误率。
例题 \(8\):
我们把一次跑步分为两个部分:上升部分和下降部分。
假设一次跑步为 \(s\to t\),记节点 \(x\) 的深度为 \(dep_x\),对于上升部分经过的点,经过的时间为 \(dep_{x}-dep_{s}\)。如果这次跑步能被观察到,就有如下式子:
移项得到:
因此,对于一次跑步的上升部分,我们给每个节点都插入一个 \(dep_s\),这样,最后在节点 \(x\) 统计有多少插入到元素等于 \(dep_x+w_x\) 即可。我们发现,树上路径修改,查询只有最终一次,还是树上差分。因此,插入的元素需要用桶来存储,所以又需要使用动态开点权值线段树加线段树合并。
对于下降部分,我们同样进行以下推导:
移项得到:
因此,对于一次跑步的下降部分,我们给每个节点都插入一个 \(dep_s-2\times dep[lca(s,t)]\),这样,最后在节点 \(x\) 统计有多少插入到元素等于 \(w_x-dep_x\) 即可。还是使用树上差分加线段树合并。
注意上升部分和下降部分的权值线段树是相互独立的,不能混用。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,nxt;
}e[600000];
struct node
{
int v;
}tr[40000000];
int n,m,x,y,a[600000],ans[600000],rt[600000],lc[40000000],rc[40000000],h[600000],dep[600000],fa[600000][40],ce=0,cnt=0;
void add_edge(int u,int v)
{
e[++ce].nxt=h[u];
e[ce].v=v;
h[u]=ce;
}
void dfs1(int now,int f)
{
fa[now][0]=f,dep[now]=dep[f]+1;
for(int i=1;i<=30;i++)
if(fa[fa[now][i-1]][i-1]!=0)fa[now][i]=fa[fa[now][i-1]][i-1];
else break;
for(int i=h[now];i;i=e[i].nxt)
if(e[i].v!=f)dfs1(e[i].v,now);
}
int lca(int x,int y)
{
if(dep[x]>dep[y])swap(x,y);
int c=dep[y]-dep[x];
for(int i=30;i>=0;i--)
if((1<<i)&c)y=fa[y][i];
if(x==y)return x;
for(int i=30;i>=0;i--)
if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
void pushup(int x)
{
tr[x].v=tr[lc[x]].v+tr[rc[x]].v;
}
void insert(int &now,int l,int r,int k,int c)
{
if(!now)now=++cnt;
if(l==r)
{
tr[now].v+=c;
return;
}
int mid=(l+r)>>1;
if(k<=mid)insert(lc[now],l,mid,k,c);
else insert(rc[now],mid+1,r,k,c);
pushup(now);
}
int query(int now,int l,int r,int k)
{
if(l==r)return tr[now].v;
int mid=(l+r)>>1;
if(k<=mid)return query(lc[now],l,mid,k);
else return query(rc[now],mid+1,r,k);
}
void merge(int x,int &y,int l,int r)
{
if(!x)return;
if(!y)
{
y=x;
return;
}
if(l==r)
{
tr[y].v+=tr[x].v;
return;
}
int mid=(l+r)>>1;
merge(lc[x],lc[y],l,mid);
merge(rc[x],rc[y],mid+1,r);
pushup(y);
}
void dfs2(int now,int f)
{
for(int i=h[now];i;i=e[i].nxt)
if(e[i].v!=f)
{
dfs2(e[i].v,now);
merge(rt[e[i].v],rt[now],-3e5,3e5);
merge(rt[e[i].v+n],rt[now+n],-3e5,3e5);
}
ans[now]+=query(rt[now],-3e5,3e5,a[now]+dep[now]);
ans[now]+=query(rt[now+n],-3e5,3e5,a[now]-dep[now]);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&x,&y);
add_edge(x,y),add_edge(y,x);
}
dfs1(1,0);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
int l=lca(x,y);
insert(rt[x],-3e5,3e5,dep[x],1);
if(fa[l][0])insert(rt[fa[l][0]],-3e5,3e5,dep[x],-1);
insert(rt[y+n],-3e5,3e5,dep[x]-2*dep[l],1);
insert(rt[l+n],-3e5,3e5,dep[x]-2*dep[l],-1);
}
dfs2(1,0);
for(int i=1;i<=n;i++)printf("%d ",ans[i]);
return 0;
}
后记
查了一下大纲,震惊了,线段树只有 \(6\) 级。
这篇成功取代 【7】同余学习笔记,共 \(1495\) 行,成为最长的学习笔记。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号