【6】树的DFS序、直径、重心
前言
树上操作是 OI 重要的一环,树的 DFS 序、直径、重心这一堆东西也是树上操作的基础。树的 DFS 序可以把树上问题转化为区间问题,树的直径的性质经常是解题的关键,树的重心可以防止一些树上算法复杂度退化——它们都是玄学但有用的算法。
树的DFS序
在一棵树上进行 DFS,按访问顺序(时间戳)将节点排成一个序列,记录某个点 第一次被访问的时候已经被访问过的点(包括这个点)的数量 和最后一次被访问的时候已经被访问过的点的数量 ,则对 及其子节点的修改可以转化为修改区间 。
例如下面这一棵树:(节点编号为时间戳)
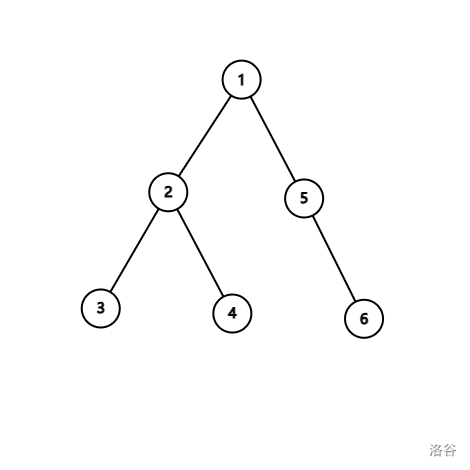
则这棵树的 DFS 序为:
号节点的 ,那么如果想要修改 号节点以及其子树,那么修改区间 即可。
代码实现也很简单, 可以在节点 递归进入的时候求出, 可以在递归结束的时候求出,代码就不放了。其实是没有对应的题目,代码没写
树的直径
定义:树上两点之间的最长简单路径是树的直径。
求法:
:两次 DFS
从任意一个节点出发,求出距离该节点最远的的节点 。再从节点 出发,求出距离该节点最远的的节点 。则 之间的简单路径就是的树的直径。证明
void dfs(long long root,long long pre)
{
for(long long i=h[root];i;i=e[i].next)
if(pre!=e[i].t)
{
dis[e[i].t]=dis[root]+e[i].dis;
dfs(e[i].t,root);
}
}
long long diameter(long long st)
{
memset(dis,0,sizeof(dis));now=0;
dfs(st,0);
for(int i=1;i<=n;i++)
if(dis[i]>now)now=dis[i],y=i;
memset(dis,0,sizeof(dis));now=0;
dfs(y,0);
for(int i=1;i<=n;i++)
if(dis[i]>now)now=dis[i];
return now;
}
优点:可以求出直径具体经过了哪些顶点,略微修改即可。
void dfs(long long root,long long pre)
{
prv[root]=pre;
for(long long i=h[root];i;i=e[i].next)
if(pre!=e[i].t)
{
dis[e[i].t]=dis[root]+e[i].dis;
dfs(e[i].t,root);
}
}
void diameter(long long st)
{
memset(dis,0,sizeof(dis));now=0;
dfs(st,0);
for(int i=1;i<=n;i++)
if(dis[i]>now)now=dis[i],y=i;
memset(dis,0,sizeof(dis));now=0;
dfs(y,0);
long long z=0;
for(int i=1;i<=n;i++)
if(dis[i]>now)now=dis[i],z=i;
now=z;
while(now!=0)
{
lu[++l]=now;
now=prv[now];
}
}
缺点:不能处理负权边。
:树形 DP
根据树的直径的定义,以某个点为两点间的公共祖先,则树的直径的长度为树中某个点与间的最长简单路径长度和次长简单路径长度之和的最大值。
原因显然:如果两点要相连,那么必定需要经过一个公共祖先。在这个公共祖先的角度看来,需要贪心地选择最长简单路径和次长简单路径,才能保证求出以这个点为公共祖先的两点之间的最长路径长度。
由于每个点都有可能成为直径中的公共祖先,而且需要求出树中的距离,考虑使用树形 DP,依次求解每一个点。
void dp(long long root,long long pre)
{
for(int i=h[root];i;i=e[i].next)
{
if(e[i].t==pre)continue;
dp(e[i].t,root);
if(d1[root]<d1[e[i].t]+e[i].dis)d2[root]=d1[root],d1[root]=d1[e[i].t]+e[i].dis;
else if(d2[root]<d1[e[i].t]+e[i].dis)d2[root]=d1[e[i].t]+e[i].dis;
now=max(now,d1[root]+d2[root]);
}
}
优点:可以处理负权边。
缺点:不能求出直径具体经过了哪些顶点。
两个算法的时间复杂度均为 。
树的重心
定义:找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心。
性质:
:删去重心后,生成的多棵树能尽可能平衡,用于防止树上算法(如点分治)退化。
: 树上所有的点到树的重心的距离之和是最短的,如果有多个重心,那么总距离相等。
:插入或删除一个点,树的重心的位置最多移动一个单位。
:若添加一条边连接 棵树,那么新树的重心一定在原来两棵树的重心的路径上。
求法:
从任何一个点开始 DFS。对于每一个点,通过 DFS 求出其每一棵子树的大小,并取最大值。由于以这个点为重心时该节点的父节点以及其祖先也是一棵子树,所以还需要通过总的节点数减去该节点子树节点数之和(包括这个节点)。最后,在每个节点处取最小值即可。
int dfs(int root,int pre)
{
int maxn=0;
for(int i=h[root];i;i=e[i].next)
if(e[i].t!=pre)
{
int z=dfs(e[i].t,root);
s[root]+=z,maxn=max(maxn,z);
}
ans=min(ans,max(maxn,n-s[root]));
return s[root];
}
时间复杂度:
例题
例题 :
树的直径模板题,注意有负权边,需要使用树形 DP。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
long long next,t,dis;
}e[80010];
long long n=0,cnt=0,now=-99999999,d1[40010],d2[40010],h[40010];
void add_edge(long long u,long long v,long long dis)
{
e[++cnt].next=h[u];
e[cnt].t=v;
e[cnt].dis=dis;
h[u]=cnt;
}
void dp(long long root,long long pre)
{
for(int i=h[root];i;i=e[i].next)
{
if(e[i].t==pre)continue;
dp(e[i].t,root);
if(d1[root]<d1[e[i].t]+e[i].dis)d2[root]=d1[root],d1[root]=d1[e[i].t]+e[i].dis;
else if(d2[root]<d1[e[i].t]+e[i].dis)d2[root]=d1[e[i].t]+e[i].dis;
now=max(now,d1[root]+d2[root]);
}
}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n-1;i++)
{
long long u,v,dis;
scanf("%lld%lld%lld",&u,&v,&dis);
add_edge(u,v,dis);
add_edge(v,u,dis);
}
dp(1,0);
printf("%lld",now);
return 0;
}
例题 :
树的重心模板题,不多赘述。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int t,next,dis;
}e[200010];
int n,h[200010],s[200010],cnt=0,ans=99999999;
void add_edge(int u,int v,int dis)
{
e[++cnt].next=h[u];
e[cnt].t=v;
e[cnt].dis=dis;
h[u]=cnt;
}
int dfs(int root,int pre)
{
int maxn=0;
for(int i=h[root];i;i=e[i].next)
if(e[i].t!=pre)
{
int z=dfs(e[i].t,root);
s[root]+=z,maxn=max(maxn,z);
}
ans=min(ans,max(maxn,n-s[root]));
return s[root];
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n-1;i++)
{
int u=0,v=0;
scanf("%d%d",&u,&v);
add_edge(u,v,1);
add_edge(v,u,1);
}
for(int i=1;i<=n;i++)s[i]=1;
dfs(1,0);
printf("%d",ans);
return 0;
}
例题 :
由于数据范围很小,所以可以考虑暴力一点的做法。
可以直接使用 Floyd 算法求出任意两点之间的最长路,然后直接求最大值,记录两端节点,就求出了树的直径。
从两个节点中的任意一个出发,用 数组记录每个点是由哪一个点搜索来的。搜索完成后,从另一个节点通过 反向推回去,记录通过的节点数,就得到了树的直径经过的点的序列。
还有一个显然易见的贪心,就是选树网的核时应该选取不超过 的最长的一段。因为如果将不超过 的最长的一段中减去一部分,那么一定会有一部分点到树网的核的距离变长,结果一定比不减去差。
然后考虑双指针尺取每一段,在树的直径经过的点的序列从左往右枚举终点,并通过变化量求出对应的起点。可以直接枚举双指针取出的这一段中的节点与树中的每一个节点的距离(通过 Floyd 进行 查询),按照题目要求的方式求解。
时间复杂度为 ,可以通过。
#include <bits/stdc++.h>
using namespace std;
long long n=0,s=0,cnt=0,now=0,x=0,y=0,h=1,t=1,sum=0,ans=99999999,lu[410],l=0,dis[410],d[410][410],f[410][410],prv[410];
void dfs(long long root,long long pre)
{
prv[root]=pre;
for(long long i=1;i<=n;i++)
if(d[root][i]&&pre!=i)dfs(i,root);
}
int main()
{
scanf("%lld%lld",&n,&s);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i==j)f[i][j]=0;
else f[i][j]=99999999;
for(int i=1;i<=n-1;i++)
{
long long u,v,dis;
scanf("%lld%lld%lld",&u,&v,&dis);
f[u][v]=f[v][u]=dis,d[u][v]=d[v][u]=1;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(f[i][j]>now)now=f[i][j],x=i,y=j;
dfs(x,0);
now=y;
while(now!=0)
{
lu[++l]=now;
now=prv[now];
}
while(sum<=s&&t<=l)sum+=f[lu[t]][lu[t+1]],t++;
t--,sum-=f[lu[t]][lu[t+1]];
while(t<=l)
{
long long tol=0;
for(int k=1;k<=n;k++)
{
long long cnt=99999999;
for(int j=h;j<=t;j++)
cnt=min(cnt,f[lu[j]][k]);
tol=max(tol,cnt);
}
ans=min(ans,tol);
sum+=f[lu[t]][lu[t+1]],t++;
while(sum>s)sum-=f[lu[h]][lu[h+1]],h++;
}
printf("%lld",ans);
return 0;
}
例题 :
例题 加强版。观察发现,例题 做法的瓶颈是 Floyd(),可优化的地方是枚举双指针取出的这一段中的节点与树中的每一个节点的距离()。
如果以树的直径的一个端点为根,那么可以发现每个非直径节点最近的直径节点均为其父节点。如下图所示:(加粗的为直径)
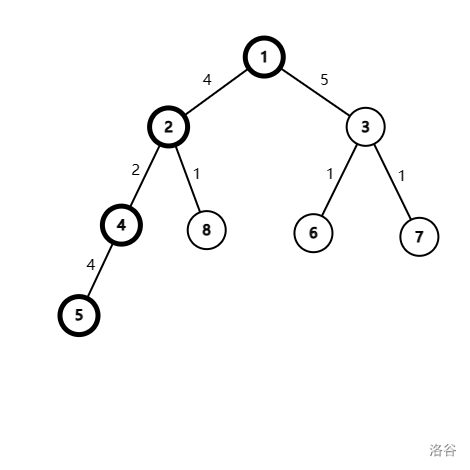
我们可以通过 DFS 求出距离每个直径节点最远的节点的距离,记为 。具体方法就是以树的直径的一个端点为根,递归累加求出每个节点到最近的直径祖先的距离,然后通过返回最大值进行比较。由于直径中的节点在这一步中不用考虑,所以当目前节点为直径节点时,需要重置距离为 ,并且返回 。这样,时间复杂度就降低到了 。
我们还是可以双指针尺取每一段,并比较每一段中每一个节点的 。此时,我们需要考虑不在枢纽上,但在直径中的节点。这样的节点有两类:一类是在当前尺取区间之前的,其最大值用 来维护;另类是在当前尺取区间之后的,其最大值用 来维护
对于每一个不在枢纽上,但在直径中的节点,其实际的 的值为这个点加上其最近的枢纽节点与这个节点的距离。具体来说,在当前尺取区间之前的,其实际的 的值为这个点加上尺取区间最后的节点与这个节点的距离;在当前尺取区间之后的,其实际的 的值为这个点加上尺取区间最前的节点与这个节点的距离。这个可以使用前缀和来维护。
当尺取区间向前推进时,必然有新的节点成为在当前尺取区间之前的节点。我们可以在处理完 的变化(加上尺取区间最后的节点推进时走过的边的边权)后比较新加入节点和原最大值 ,若更大,则更新 。
当尺取区间向前推进时,必然有新的节点不再是在当前尺取区间之后的节点。对于这类节点,我们只需要处理 的变化(减去尺取区间最前的节点推进时走过的边的边权)就可以了。原因是在当前尺取区间之后的节点在区间推进时必然同时减少,差值不变,最大值依旧是最大值。即使有些节点不再是在当前尺取区间之后的节点,那么不会影响最大值。即使是没有在当前尺取区间之后的节点,那么 ,也会被用于记录的变量的初始值 覆盖掉,不会影响结果。
最后,每次还需要遍历前尺取区间的每一个节点,以确保树中每一个节点都被算过。总体时间复杂度为 。
在此题中,虽然没有用到任何高级算法,但是依旧实现了 做法,也算是一个基础大综合了。
另外,注意一下代码中用 Hash 来直接查询两点之间连边的编号的处理技巧,这十分常用。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
long long next,t,dis;
}e[600060];
long long n=0,cnt=0,now=0,y=0,s=0,ans=99999999,sum=0,sn[400020],dis[400020],h[400020],prv[400020],lu[400020],mx[400020],l=0;
bool book[400020];
unordered_map<long long,long long>d;
long long makepair(long long x,long long y)
{
return x*3500000+y;
}
void add_edge(long long u,long long v,long long dis)
{
e[++cnt].next=h[u];
e[cnt].t=v;
e[cnt].dis=dis;
h[u]=cnt;
d[makepair(u,v)]=cnt;
}
void dfs(long long root,long long pre)
{
prv[root]=pre;
for(long long i=h[root];i;i=e[i].next)
if(pre!=e[i].t)
{
dis[e[i].t]=dis[root]+e[i].dis;
dfs(e[i].t,root);
}
}
long long getdis(long long root,long long pre)
{
if(book[root])dis[root]=0;
for(long long i=h[root];i;i=e[i].next)
if(pre!=e[i].t)
{
dis[e[i].t]=dis[root]+e[i].dis;
mx[root]=max(mx[root],getdis(e[i].t,root));
}
mx[root]=max(mx[root],dis[root]);
return book[root]?0:mx[root];
}
void work(long long st)
{
memset(dis,0,sizeof(dis));now=0;
dfs(st,0);
for(int i=1;i<=n;i++)
if(dis[i]>now)now=dis[i],y=i;
memset(dis,0,sizeof(dis));now=0;
dfs(y,0);
long long z=0;
for(int i=1;i<=n;i++)
if(dis[i]>now)now=dis[i],z=i;
now=z;
while(now!=0)
{
lu[++l]=now;
book[now]=1;
now=prv[now];
}
memset(dis,0,sizeof(dis));
getdis(y,0);
for(int i=1;i<=l-1;i++)sn[i+1]=sn[i]+e[d[makepair(lu[i],lu[i+1])]].dis;
long long h=1,t=1,mz=0,my=0;
while(sum<=s&&t<=l)sum+=e[d[makepair(lu[t],lu[t+1])]].dis,t++;
t--,sum-=e[d[makepair(lu[t],lu[t+1])]].dis;
for(int i=t+1;i<=l;i++)my=max(my,mx[lu[i]]+sn[i]-sn[t]);
while(t<=l)
{
long long tol=max(mz,my);
vector<long long>ad;
for(int i=h;i<=t;i++)tol=max(tol,mx[lu[i]]);
ans=min(ans,tol);
sum+=e[d[makepair(lu[t],lu[t+1])]].dis,my-=e[d[makepair(lu[t],lu[t+1])]].dis,t++;
while(sum>s)
{
ad.push_back(h);
sum-=e[d[makepair(lu[h],lu[h+1])]].dis,h++;
}
int q=ad.size();
if(q!=0)mz+=(sn[h]-sn[ad[0]]);
for(int i=0;i<q;i++)mz=max(mz,mx[lu[ad[i]]]+sn[h]-sn[ad[i]]);
}
}
int main()
{
scanf("%lld%lld",&n,&s);
for(int i=1;i<=n-1;i++)
{
long long u=0,v=0,d=0;
scanf("%lld%lld%lld",&u,&v,&d);
add_edge(u,v,d);
add_edge(v,u,d);
}
work(1);
printf("%lld",ans);
return 0;
}
例题 :
观察 的范围,发现 只有 和 两种取值,可以分类讨论。
在两个点之间添加一条新的边,使到达其中一个点时可以直接到达另一个点,省略回溯的路程。也就是说,每添加一条边,总结果就会减少这两点之间的路径长度。当 时,根据贪心,只需要求出两点间最长的路径长度,也就是树的直径的长度,用原需要走的路程减去即可,注意增加的这条路本身也算作路程。
当 时,需要考虑第一次中树的直径中的边是否会对第二次造成影响。由于每条路都需要至少走一次,所以无论如何也要计算添加的边的两点间的距离。在第一次时走过的边,已经满足至少走一次,再走反而会额外走一条边,造成反向贡献。所以,可以把第一次走过的边赋值为 ,再计算树的直径。最后用原需要走的路程减去这两次的结果就行了,注意增加的这条路本身也算作路程。
注意第一次要使用 dfs 求直径,因为要求出具体经过了哪些边。第二次要用树形 dp,因为 dfs 无法处理 这种负权边。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
long long next,t,dis;
}e[200020];
long long n=0,k=0,y=0,cnt=0,now=-99999999,now2=-99999999,dis[200020],d1[200020],d2[200020],h[200020],prv[200020];
unordered_map<long long,long long>d;
void add_edge(long long u,long long v,long long dis)
{
e[++cnt].next=h[u];
e[cnt].t=v;
e[cnt].dis=dis;
h[u]=cnt;
d[u*200000+v]=cnt;
}
void dp(long long root,long long pre)
{
for(int i=h[root];i;i=e[i].next)
{
if(e[i].t==pre)continue;
dp(e[i].t,root);
if(d1[root]<d1[e[i].t]+e[i].dis)d2[root]=d1[root],d1[root]=d1[e[i].t]+e[i].dis;
else if(d2[root]<d1[e[i].t]+e[i].dis)d2[root]=d1[e[i].t]+e[i].dis;
now=max(now,d1[root]+d2[root]);
}
}
void dfs(long long root,long long pre)
{
prv[root]=pre;
for(long long i=h[root];i;i=e[i].next)
if(pre!=e[i].t)
{
dis[e[i].t]=dis[root]+e[i].dis;
dfs(e[i].t,root);
}
}
int main()
{
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n-1;i++)
{
long long u,v;
scanf("%lld%lld",&u,&v);
add_edge(u,v,1);
add_edge(v,u,1);
}
if(k==1)
{
dp(1,0);
printf("%lld",(n-1)*2-(now-1));
}
else if(k==2)
{
dfs(1,0);
for(int i=1;i<=n;i++)
if(dis[i]>now2)now2=dis[i],y=i;
memset(dis,0,sizeof(dis));now2=-99999999;
dfs(y,0);
long long z=0;
for(int i=1;i<=n;i++)
if(dis[i]>now2)now2=dis[i],z=i;
long long nw=z,pr=z;
while(nw!=0)
{
nw=prv[nw];
long long bz=max(pr,nw),sz=min(pr,nw);
if(sz==0)break;
e[d[bz*200000+sz]].dis=-1;
e[d[sz*200000+bz]].dis=-1;
pr=nw;
}
dp(1,0);
printf("%lld",(n-1)*2-(now-1)-(now2-1));
}
return 0;
}
后记
绘图工具(图片来源)




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!