DS博客作业05--查找
0.PTA得分截图

1.本周学习总结
1.1 总结查找内容
-
查找的性能指标ASL:
- 顺序查找成功的总查找次数为n(n+1)/2,所以查找成功的ASL为(n+1)/2。
- 顺序查找不成功的总查找次数为n^2,所以查找失败的ASL为n。
- 二分查找的成功ASL和不成功ASL需要根据所画出的判断树来进行计算,例如:有一个有序表{1,3,9,12,32,41,45,62,75,77,82,95,99},则构造出的二分判定树如下图所示:
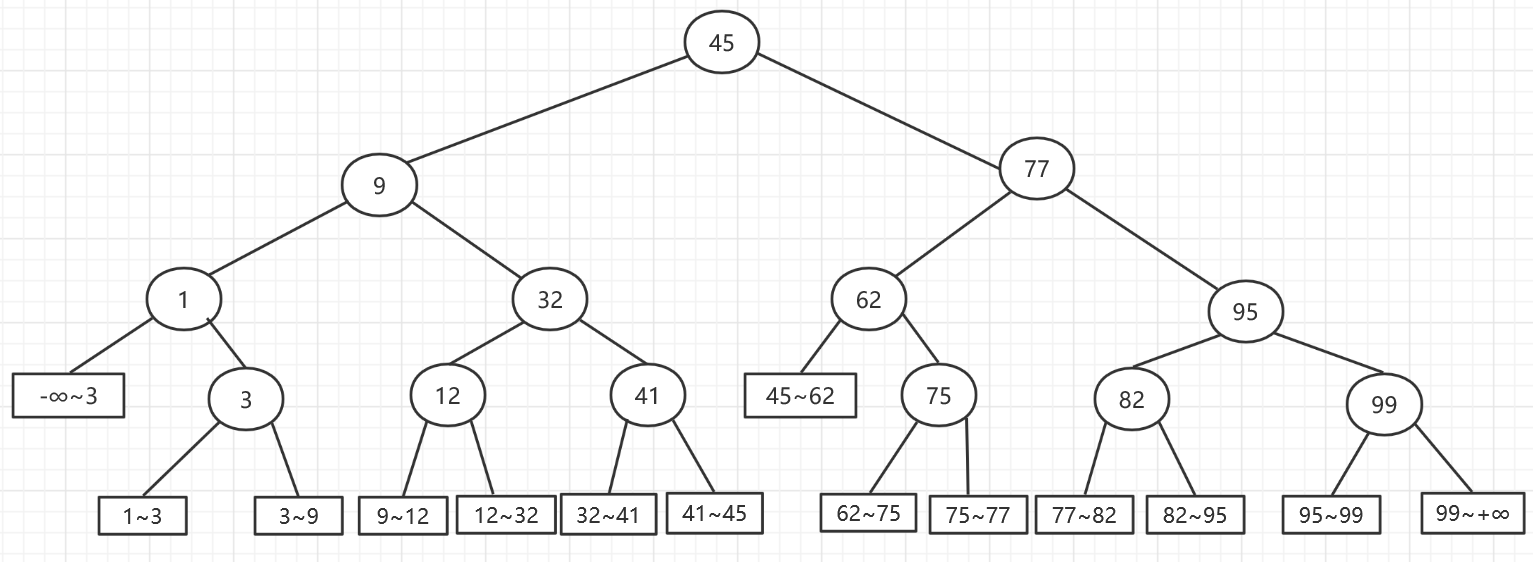
则此时查找成功的ASL为:(1x1+2x2+3x4+4x6)/13=3.1
而查找不成功的ASL为:(3x2+4x12)/14=3.8
-
动态查找:二叉搜索树
-
二叉搜索树的构建:二叉搜索树要满足每个节点的左子树中的所有节点都小于该节点,右子树中的所有节点都大于该节点。在构建二叉搜索树时,根据元素的大小将元素插入到左右子树中。例如:在一棵空的二叉搜索树中依次插入关键字序列为{12,7,17,11,16,2,13,9,21,4},结果如下图所示:
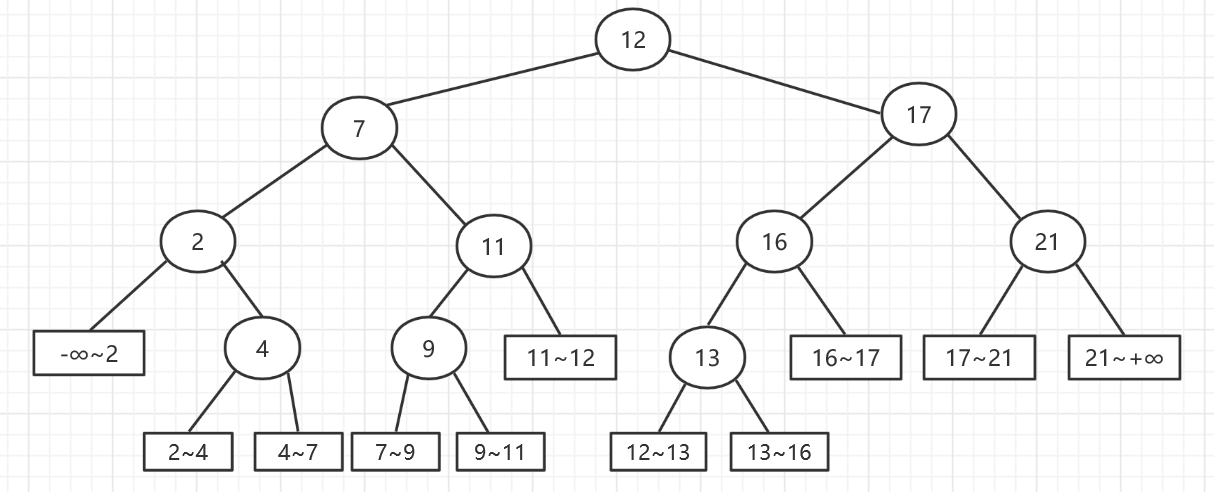
二叉搜索树的建树代码为:void CreateTree(BinTree& BST, int N) { for ( i=0; i<N; i++ ) { scanf("%d", &X); BST = Insert(BST, X); } } BinTree Insert(BinTree BST, ElementType X) { if (BST == NULL) { BST = (BinTree)malloc(sizeof(struct TNode)); BST->Data = X; BST->Left = NULL; BST->Right = NULL; } else if (BST->Data > X) //X要插入BST的左子树中 { BST->Left = Insert(BST->Left, X); } else //X要插入BST的右子树中 { BST->Right = Insert(BST->Right, X); } return BST; } -
二叉搜索树的插入:元素需要插入在二叉搜索树的叶子节点位置,需要从根节点开始比较,如果比比较节点小则继续跟比较节点的左孩子比较,如果比比较节点大则继续跟比较节点的右孩子比较,直到插入比较的节点为空,则插入该位置。代码如下所示:
BinTree Insert(BinTree BST, ElementType X) { if (BST == NULL) { BST = (BinTree)malloc(sizeof(struct TNode)); BST->Data = X; BST->Left = NULL; BST->Right = NULL; } else if (BST->Data > X) //X要插入BST的左子树中 { BST->Left = Insert(BST->Left, X); } else //X要插入BST的右子树中 { BST->Right = Insert(BST->Right, X); } return BST; } -
二叉搜索树的删除:二叉树的删除要分为三种情况:(1).被删的节点是叶子节点;(2).被删的节点只有左子树或右子树;(3).被删的节点左右子树都存在
(1).被删的节点为叶子节点:这种情况最简单,直接删除该节点就可以,然后将其双亲节点的相应指针域置为空。
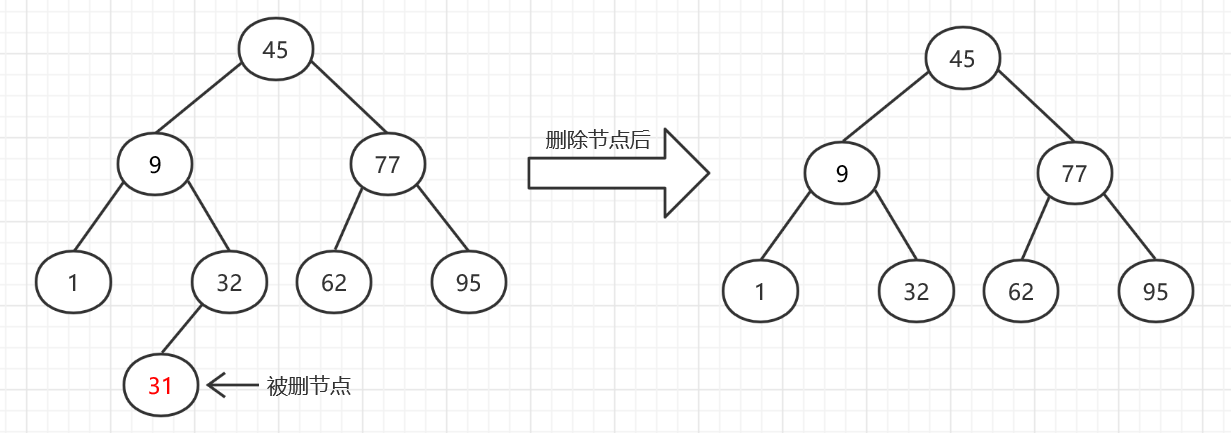
(2).被删的节点只有左子树或右子树:这种情况下,需要用该节点的左右子树替代它,即让删除节点的双亲节点的相应指针域指向该节点的左孩子或右孩子。
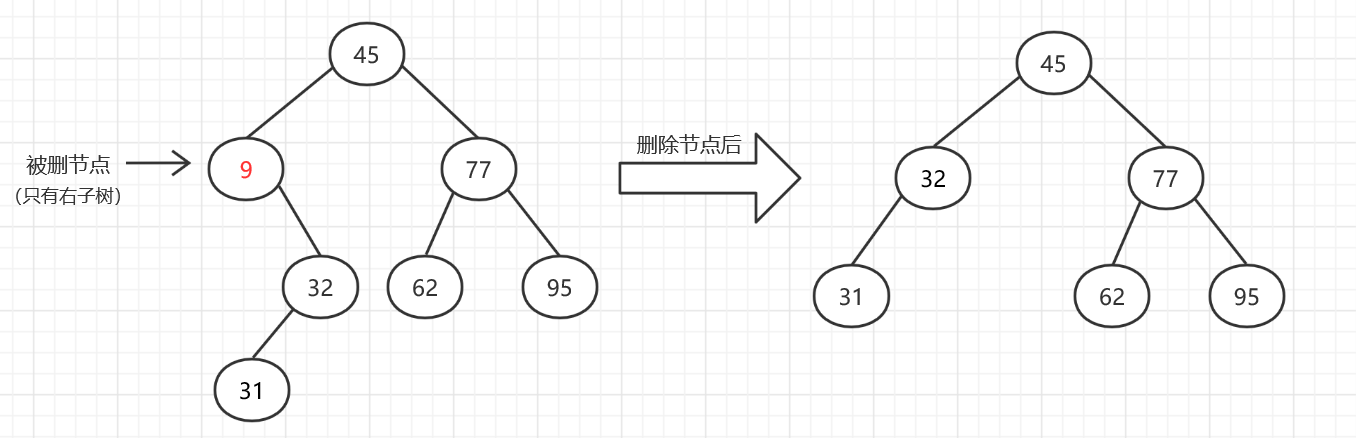
(3).被删的节点左右子树都存在:这种情况,我们需要找到被删节点其左子树中最大的节点或者右子树中最小的节点,然后用这个节点代替被删节点。
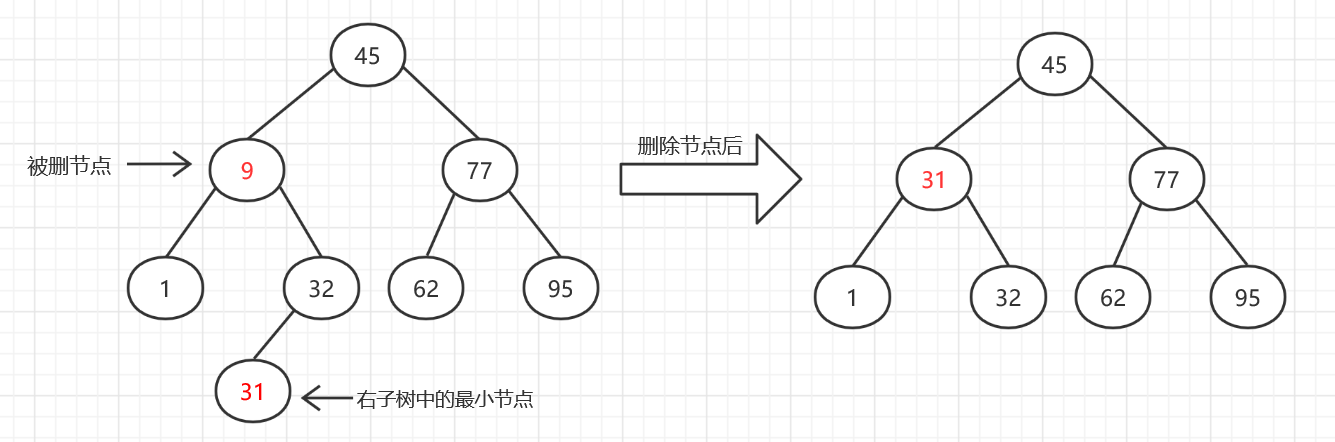
具体实现代码:
BinTree Delete(BinTree BST, ElementType X) { BinTree ptr; if (BST == NULL) { printf("Not Found\n"); } else if (BST->Data == X) { if (BST->Left && BST->Right) //被删节点的左右子树都不为空 { ptr = FindMin(BST->Right); BST->Data = ptr->Data; BST->Right = Delete(BST->Right, BST->Data); } else { ptr = BST; if (!BST->Left) //左子树为空 { BST = BST->Right; } else { BST = BST->Left; } free(ptr); } } Position FindMin(BinTree BST) { if (BST == NULL) { return NULL; } Position minPosition; minPosition = BST; while (minPosition->Left != NULL) { minPosition = minPosition->Left; } return minPosition; }
-
-
AVL树的定义:AVL树是一棵树中任意节点的左右子树高度差都不超过1的平衡二叉搜索树,所以在构建AVL树的过程中我们要对树进行调整,以保证任意节点的左右子树高度差都不超过1,我们将这种调整平衡的过程称为平衡旋转,AVL树有4种平衡旋转。
-
LL平衡旋转:当节点A左子树的左子树上插入了一个节点使A失衡,这时我们应该进行LL型调整。调整方法分为三步:(1).将A的左孩子B右上旋转到A的位置;(2).A向右下旋转,成为B的右孩子;(3).B的右孩子成为A的左孩子。

-
RR平衡旋转:当节点A右子树的右子树上插入了一个节点使A失衡,这时我们应该进行RR型调整。调整方法分为三步:(1).将A的右孩子B左上旋转到A的位置;(2).A向左下旋转,成为B的左孩子;(3).B的左孩子成为A的右孩子。
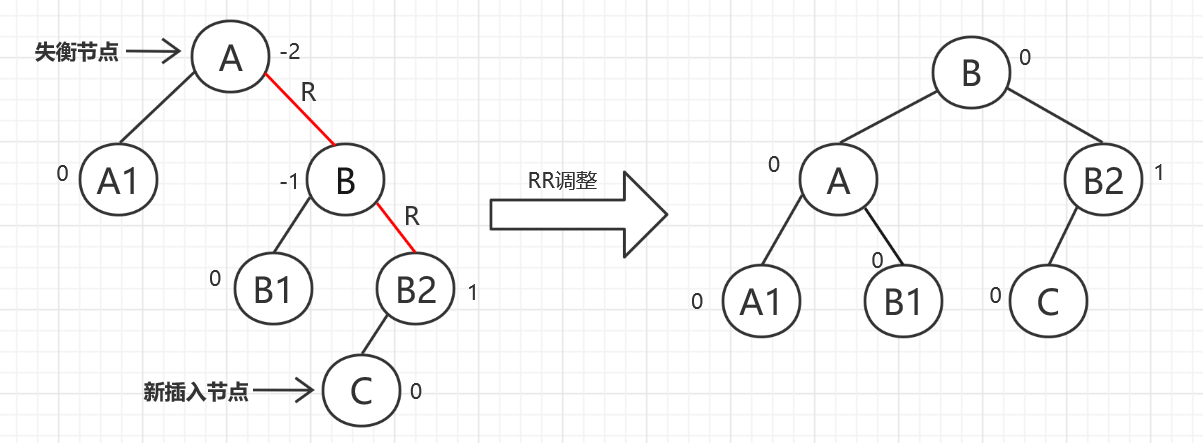
-
LR平衡旋转:当节点A左子树的右子树上插入了一个节点使A失衡,这时我们应该进行LR型调整。调整方法分为四步:(1).将A的孙子节点C向上调整到A的位置,A的左孩子B成为C的左孩子;(2).A向右下旋转,成为C的右孩子;(3).C的右孩子成为A的左孩子;(4).C的左孩子成为B的右孩子。
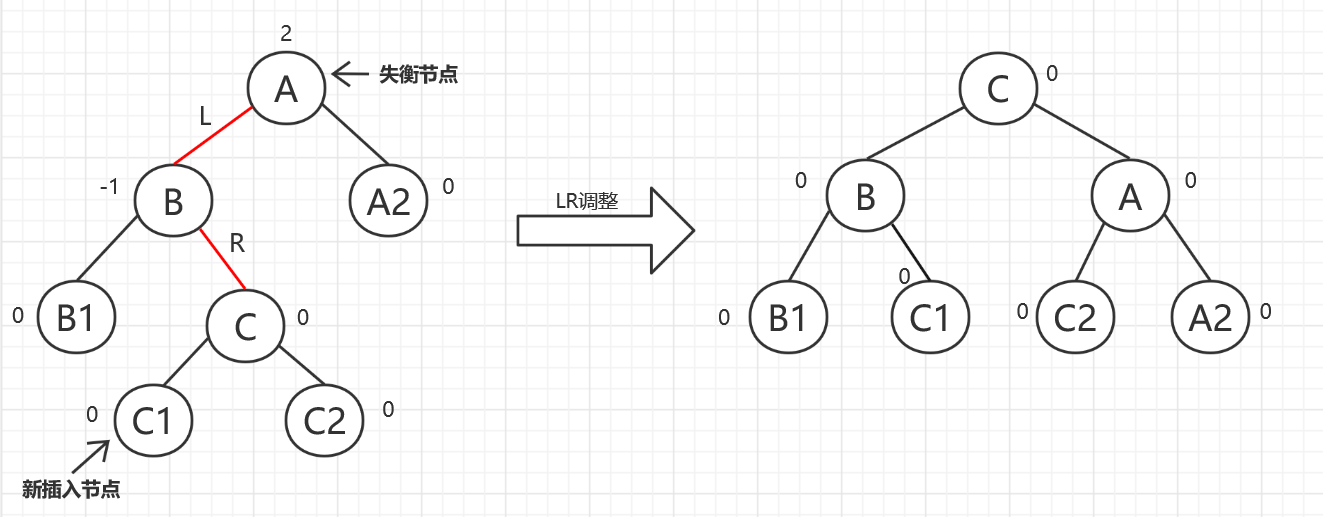
-
RL平衡旋转:当节点A右子树的左子树上插入了一个节点使A失衡,这时我们应该进行RL型调整。调整方法分为四步:(1).将A的孙子节点C向上调整到A的位置,A的右孩子B成为C的右孩子;(2).A向左下旋转,成为C的左孩子;(3).C的右孩子成为B的左孩子;(4).C的左孩子成为A的右孩子。
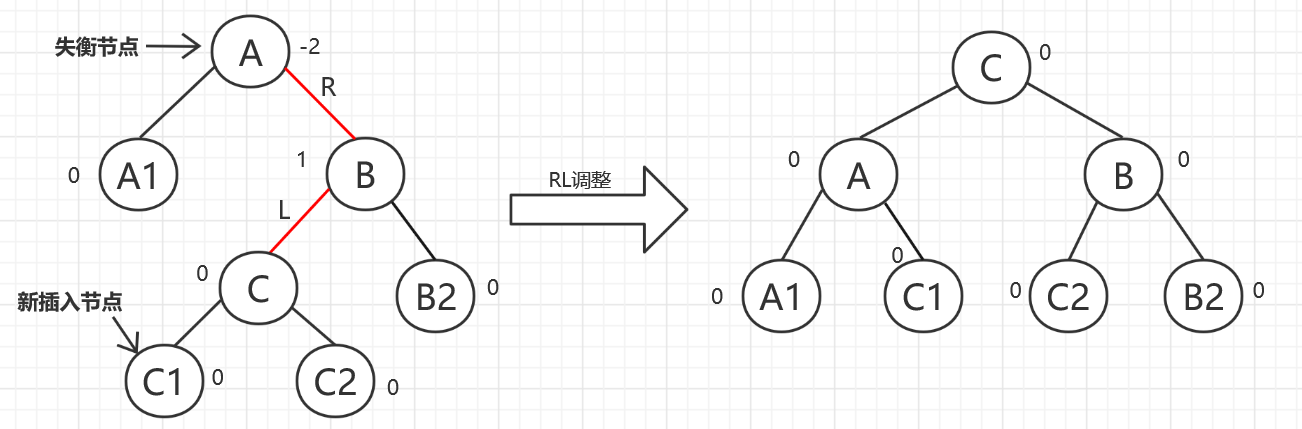
-
总结:LL和RR型都是以失衡节点的孩子为旋转轴,LR和RL型都是以失衡节点的孙子为旋转轴。
-
-
B-树和B+树定义:B-树和B+树与我们之前所学习的BST树、AVL树最大的不同就是B树的一个节点可以存放多个关键字,这样就可以降低树的高度,适用于大数据的查找。
-
对于一棵m阶B-树来说,除根节点以外每个节点最多m个孩子节点,至少m/2个孩子节点(至多m-1个关键字,至少m/2-1个关键字)。若根节点不是叶子节点,根节点至少两个孩子节点。
-
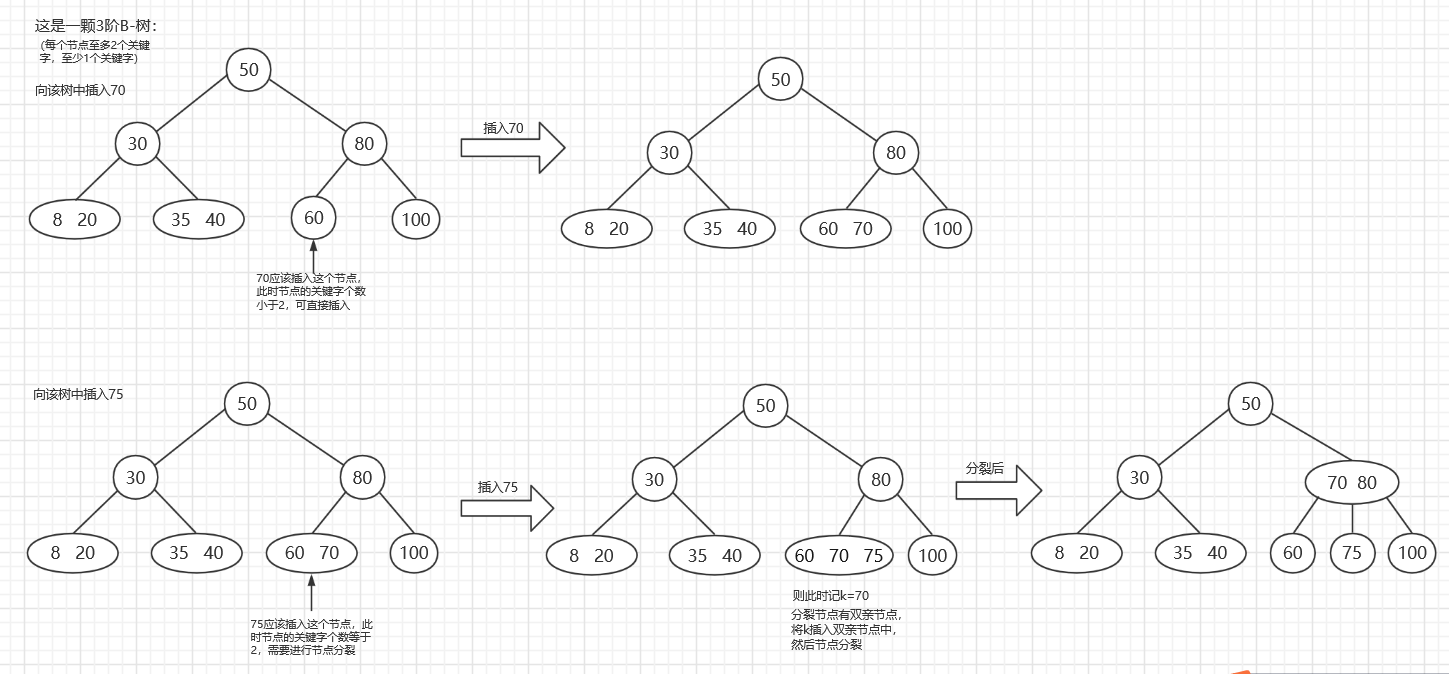
B-树的插入:B-树中关键字的插入位置一定在叶子节点,如果此时叶子节点已有m-1个关键字,则需要对该节点进行分裂,否则直接插入就可以。
B-树节点的分裂需要先取出插入新元素后位于中间位置的元素,记为k。如果分裂节点有双亲,则将k插入双亲节点中,否则新建一个双亲节点,值为k。然后将分裂节点中位于k左右的元素分别装载在左右孩子节点中。
-
B-树的删除:如果删除结点中关键字的个数>m/2-1,则直接删除。如果结点中关键字的个数=m/2-1,则要从其左右兄弟中借关键字,如果左右兄弟借不了则需要合并节点。

-
-
散列查找:散列表也称哈希表,主要适合记录的关键字与存储地址存在某种函数关系的数据。
-
哈希表的构造:哈希表的装填因子α=存储的记录个数/哈希表的大小=n/m, α越小,冲突可能性就越小; α越大(最大可取1),冲突的可能性就越大。
我们可以用除留余数法构造哈希表。除留余数法是用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址的方法。例如:设哈希函数h(k)=k mod p,h(k)为k在哈希表中的下标,若该地址中已有函数,则向后线性探测,将k存入到第一个空的地址中。
将关键字序列{7,8,30,11,18,9,14}存储到哈希表中,哈希函数为:H(key)=(key x 3)mod 7,处理冲突采用线性探测再散列法,要求装填(载)因子为0.7。则构造出的哈希表如下图所示:

此时查找成功的ASL为:(1+2+1+1+1+3+3)/7=1.71
而查找不成功的ASL为:(3+2+1+2+1+5+4)/7=18/7构造哈希表的代码: void CreateHT(HashTable ha, KeyType x[], int n, int m, int p) //创建哈希表,x为输入数组,n输入数据个数,m为哈希表长度,这里假设m=p { int i; int count = 0; for (i = 0; i < m; i++) { ha[i].key = -1; ha[i].count = 0; } for (i = 0; i < n; i++) { InsertHT(ha, count, x[i], p); } } void InsertHT(HashTable ha, int& n, KeyType k, int p) //哈希表插入数据,n表示哈希表数据个数,k插入关键字,p除数 { int h; h = k % p; uns_count = 0; if (ha[h].count == 0) { ha[h].key = k; ha[h].count = 1; } else { h = (h + 1) % p; uns_count++; while (1) { if (ha[h].count == 0) { ha[h].key = k; ha[h].count = uns_count + 1; break; } h = (h + 1) % p; uns_count++; } } n++; } -
哈希链的构造:哈希表在存储数据是会产生冲突,需要进行线性探测或者其他解决冲突的方法。而哈希链不需要,哈希函数相同的节点都存在对应节点所对应的哈希链里。
设一组初始记录关键字集合为(25,10,8,27,32,68),散列表的长度为8,散列函数H(k)=k mod 7,则构造出的哈希链如下图所示:
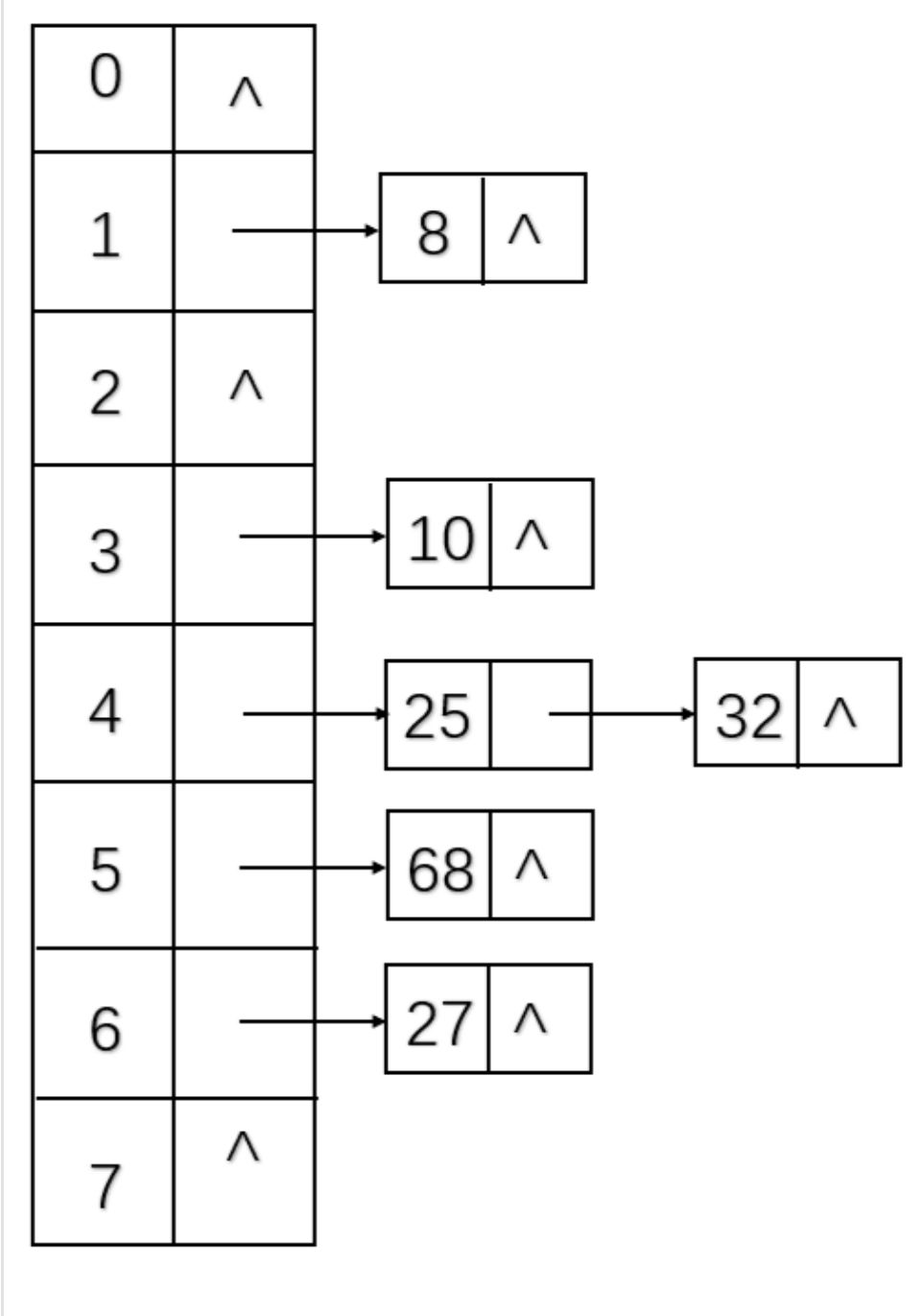
此时查找成功的ASL为:(1+1+1+1+1+2)/6=1.17
而查找不成功的ASL为:(0+1+0+1+2+1+1+0)/7=0.86哈希链的构造函数: void InsertHT(HashTable ha[], int& n, int p, KeyType k) //将关键字k插入到哈希表中 { int adr; adr = k % p; //计算哈希函数值 NodeType* q; q = (NodeType*)malloc(sizeof(NodeType)); q->key = k; //创建一一个结点q存放关键字k q->next = NULL; if (ha[adr].firstp == NULL) //若单链表adr为空 ha[adr].firstp = q; else //若单链表adr不空 { q->next = ha[adr].firstp; //采用头插法插人到ha[adr]的单链表中 ha[adr].firstp = q; } n++; //哈希表中结点的总个数增1 } void CreateHT(HashTable ha[], int& n, int m, int p, KeyType keys,int nl) //由关键字序列keys[0..nl- 1]创建哈希表 { for (int i = 0; i < m; i++) //哈希表置初值 ha[i].firstp = NULL; n = 0; for (i = 0; i < nl; i++) InsertHT(ha, n, p, keys[i]); //插入n个关键字 }
-
1.2 谈谈你对查找的认识及学习体会
查找这一章我觉得重要的还是要多做题,像AVL树的四种调整,看着课件的时候可能觉得迷迷糊糊地、似懂非懂,但结合具体的题目去一步一步调就会慢慢理解,而且我我觉得这一章的内容会比较多,不容易记清,一定要多去做题,把图画出来加深自己的印象。
2.PTA题目介绍
2.1 二叉搜索树的最近公共祖先
2.1.1 该题的设计思路
该题会有三种情况出现:1.二叉搜索树中找不到以 U 或 V 为键值的结点;2.U 和 V 中的一个结点是另一个结点的祖先;3. U 和 V都存在,它们的最近公共祖先结点为A。
所以我们首先应该去二叉搜索树中查找U和V所在的位置,确定U和V是否存在。当二者都存在时,判断在以U为根节点的二叉搜索树中能否查找到V,以此来判断U是否为V的祖先(反之亦然)。当上述两个条件都不满足时,则U和V有最近公共祖先结点A,A为层次遍历所遇到的第一个值位于U和V之中的节点。
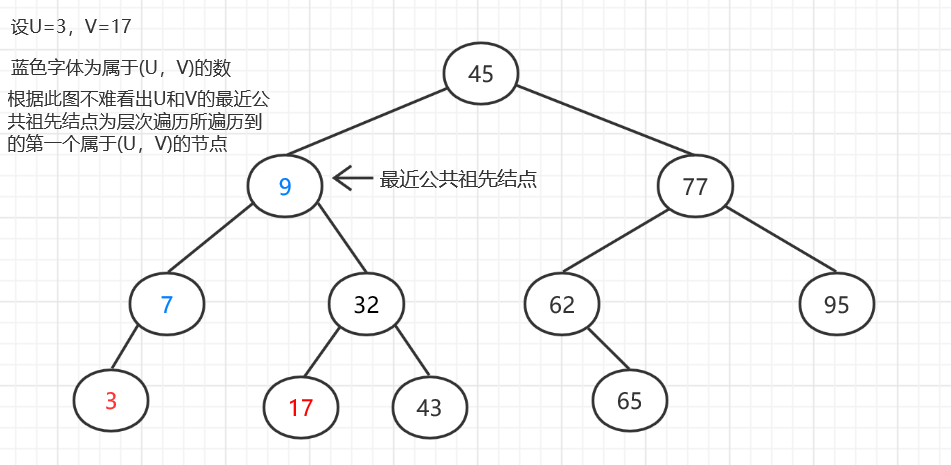
2.1.2 该题的伪代码
BinTree CreateTree(BinTree BST, int* preorder, int len) //根据二叉搜索树先序序列建二叉搜索树
{
if len==0 return NULL;
新建一个树节点BST,值为preorder序列的第一个元素,左右孩子初始化为空
找到preorder序列中大于BST->Data的值,下标为i(二叉搜索树的先序序列中,第一个大于根节点的值的后面的元素一定都在右子树)
BST->Left = CreateTree(BST->Left, preorder + 1, i - 1);
BST->Right = CreateTree(BST->Right, preorder + i, len - i);
return BST;
}
void FindAncestor(BinTree BST, int U, int V)
{
定义两个指针ptrU,ptrV分别指向U和V所在的树节点的位置。
if(ptrU或ptrV中有为空的指针)
{
输出对应结果
}
else //U和V都存在
{
判断在以ptrU为根节点的树中能否找到V /*U为V的祖先*/
判断在以ptrV为根节点的树中能否找到U /*V为U的祖先*/
if(U和V其中一个节点是另一个节点的祖先)
{
输出对应结果
}
else
{
LCA的值为用层次遍历找到第一个大于U小于V的节点
输出对应结果
}
}
}
2.1.3 具体代码

2.1.4 PTA提交列表

1.编译错误:提交时没换编译器
2.部分正确:在输出时没有加换行符导致答案错误
3.答案正确:给每个输出的地方都加了换行符后答案正确
2.1.5 本题设计的知识点
1.根据二叉搜索树先序序列建二叉搜索树:先序遍历的第一个元素一定是根节点,又因为该树为二叉搜索树,则在碰到第一个大于根节点元素的元素后面应该都为右子树元素(二叉搜索树的右子树值全大于根节点),根据该特点可将preorder序列分段,然后进行递归建树。
2.当U和V在二叉搜索树中都存在且不为对方祖先时,根据二叉搜索树的特点,它们的公共祖先应该为层序遍历时第一个碰到的值位于U和V之间的节点。
2.2 QQ帐户的申请与登陆
2.2.1 该题的设计思路
因为map容器可以将两个数据一对一的关联起来,所以本题利用map容器存储QQ号及其密码,使其具有对应关系。当用户申请新的QQ号时,先去原有容器中查找该号码是否已经存在,若不存在则将该QQ号与其对应密码存入map容器中。当用户想要登录时,同样先去原有容器中查找该号码是否已经存在,若存在则从容器中取出与该号对应的密码,与输入密码进行比较,相同则登录成功,否则失败。
2.2.2 该题的伪代码
定义map容器:map<string, string> QQ;
定义一个迭代器it:map<string, string>::iterator it;
for i=0 to i<N do
输入指令、QQ号码、密码
it = QQ.find(ID);
if(指令为N) /*要申请一个新的QQ号*/
{
if(it不为end函数返回的迭代器) /*该ID已存在*/
输出对应结果
else
用insert函数将ID和PW插入map容器,并输出对应结果
end if
}
else /*要登录原有QQ号*/
{
if(it为end函数返回的迭代器) /*该ID不存在*/
输出对应结果
else
判断it->second是否与输入的PW相同,并输出对应结果
end if
}
end for
2.2.3 具体代码

2.2.4 PTA提交列表

2.2.5 本题设计的知识点
1.map容器的用法:map是STL的一个关联容器,它提供一对一的数据处理能力。map容器的数据插入可用insert函数插入pair数据,如“QQ.insert(pair<string, string>(ID, PW))”。map容器中数据的查找可用用find函数来实现,find函数会返回数据所在位置的迭代器,如果该数据不存在,则返回end函数返回的迭代器。迭代器的定义为“map<string, string>::iterator 变量名;”
2.3 航空公司VIP客户查询
2.3.1 该题的设计思路
要定义一个结构体来存储每个用户的数据,结构体中除了用户的ID外还要有记录里程数的变量kilometer,以及构建哈希链所需要的next指针。根据每个用户的ID将用户信息存储在哈希表的对应位置,如果遇到同一用户要将里程数累加。
2.3.2 该题的伪代码
定义结构体HashNode,含ID,kilometer和指针next
定义数组hash[MAXN],初始化为NULL
定义一个flag,若flag为0则该查询人不是会员,否则输出对应里程数
for i=0 to i<N do
{
customer = new HashNode;
customer的ID和next初始化为0和NULL
输入飞行纪录
adr = customer->ID % MAXN;
if(hash[adr]为空)
customer存入hash[adr];
else
若该ID出现过则里程数累加,否则插入hash[adr]对应链的末尾;
end if
}
for i=0 to i<M do
{
flag=0; //一定要记得每次循环都初始化一次
输入查询人身份证号码ID
adr = ID % MAXN;
在hash[adr]所对应的链中查找ID,若找到则输出对应公里数且flag置为1,否则输出“No Info”
}
2.3.3 具体代码

2.3.4 PTA提交列表

1.部分正确:由于这题的一些数据比较大,如果用cin和cout来做输入输出就会导致时间效率很低,运行超时,所以在写这题时要注意使用scanf和printf来做输入输出。我后来百度了下,cin的时间效率低的原因是因为C++为了保证与C的兼容性,将cin和stdin的流进行了同步,以保证代码中混用这两个函数不会出错,但是这个同步会增加cin的耗时。解决方法除了使用scanf和printf来做输入输出外,还可以选择添加“std::ios::sync_with_stdio(false)”语句,将iostream与stdio解绑,但要注意的是,解绑之后,cin和scanf一定不能混用。
2.答案正确:将原代码中的输入部分换成用scanf读入后,答案正确。
2.3.5 本题设计的知识点
1.哈希链的建立:每输入一组数据根据哈希函数找到要存入的位置,然后链接在该链的尾部,建立哈希链。
2.哈希链的查找:输入的数据有可能在之前输入过,那么则需要进行里程数的累加,需要找到原来输入的位置,然后累加里程数。



