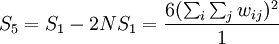Moran's I Statistics

空间分析中常见的两种统计算法，分别是Moran‘s I 和Geary’s C Statistics。
下面主要讨论前者的思想。
Moran's I (Moran 1950) is a weighted correlation coefficient used to detect departures from spatial randomness. Moran's I is used to determine whether neighboring areas are more similar than would be expected under the null hypothesis. 
在维基百科中的解释如下：

In statistics, Moran's I is a measure of spatial autocorrelation developed by Patrick A.P. Moran.[1] Like autocorrelation, spatial autocorrelation means that adjacent observations of the same phenomenon are correlated. However, autocorrelation is about proximity in time. Spatial autocorrelation is about proximity in (two-dimensional) space. Spatial autocorrelation is more complex than autocorrelation because the correlation is two-dimensional and bi-directional.

Moran's I is defined as

I = \frac{N} {\sum_{i} \sum_{j} w_{ij}} \frac {\sum_{i} \sum_{j} w_{ij}(X_i-\bar X) (X_j-\bar X)} {\sum_{i} (X_i-\bar X)^2}

where N is the number of spatial units indexed by i and j; X is the variable of interest; \bar X is the mean of X; and wij is a matrix of spatial weights.

The expected value of Moran's I under hypothesis of no spatial autocorrelation is

E(I) = \frac{-1} {N-1}

Its variance equals

Var(I) = \frac{NS_4-S_3S_5} {(N-1)(N-2)(N-3)(\sum_{i} \sum_{j} w_{ij})^2}

where

S_1 = \frac {1} {2} \sum_{i} \sum_{j} (w_{ij}+w_{ji})^2
S_2 = \frac {\sum_{i} ( \sum_{j} w_{ij} + \sum_{j} w_{ji})^2} {1}
S_3 = \frac {N^{-1} \sum_{i} (x_i - \bar x)^4} {(N^{-1} \sum_{i} (x_i - \bar x)^2)^2}
S_4 = \frac {(N^2-3N+3)S_1 - NS_2 + 3 (\sum_{i} \sum_{j} w_{ij})^2} {1}
S_5 = S_1 - 2NS_1 = \frac {6(\sum_{i} \sum_{j} w_{ij})^2} {1}

Negative (positive) values indicate negative (positive) spatial autocorrelation. Values range from −1 (indicating perfect dispersion) to +1 (perfect correlation). A zero values indicates a random spatial pattern. For statistical hypothesis testing, Moran's I values can be transformed to Z-scores in which values greater than 1.96 or smaller than −1.96 indicate spatial autocorrelation that is significant at the 5% level.

The significance of I can be judged by calculating the variance of I and then comparing the following statistic to the standard normal distribution

 

                                           .   （关于置信度的计算）

 

Moran's I is inversely related to Geary's C, but it is not identical. Moran's I is a measure of global spatial autocorrelation, while Geary's C is more sensitive to local spatial autocorrelation.


可以看出Moran’s I的相关特点。


posted on 2009-10-11 22:18  畅游九州  阅读(4678)  评论(0)  编辑  收藏  举报

导航