返回一个二维整数数组中最大子数组的和

要求：

　　 输入一个二维整形数组，数组里有正数也有负数。

　　二维数组中连续的一个子矩阵组成一个子数组，每个子数组都有一个和。

　　求所有子数组的和的最大值。要求时间复杂度为O(n)。

结对编程要求：

　　两人结对完成编程任务。

　　 一人主要负责程序分析，代码编程。 一人负责代码复审和代码测试计划。

　　发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)。

设计思路：

　　将二维整型数组求最大子数组之和化为求一位最大子数组之和。（降维）　　　　

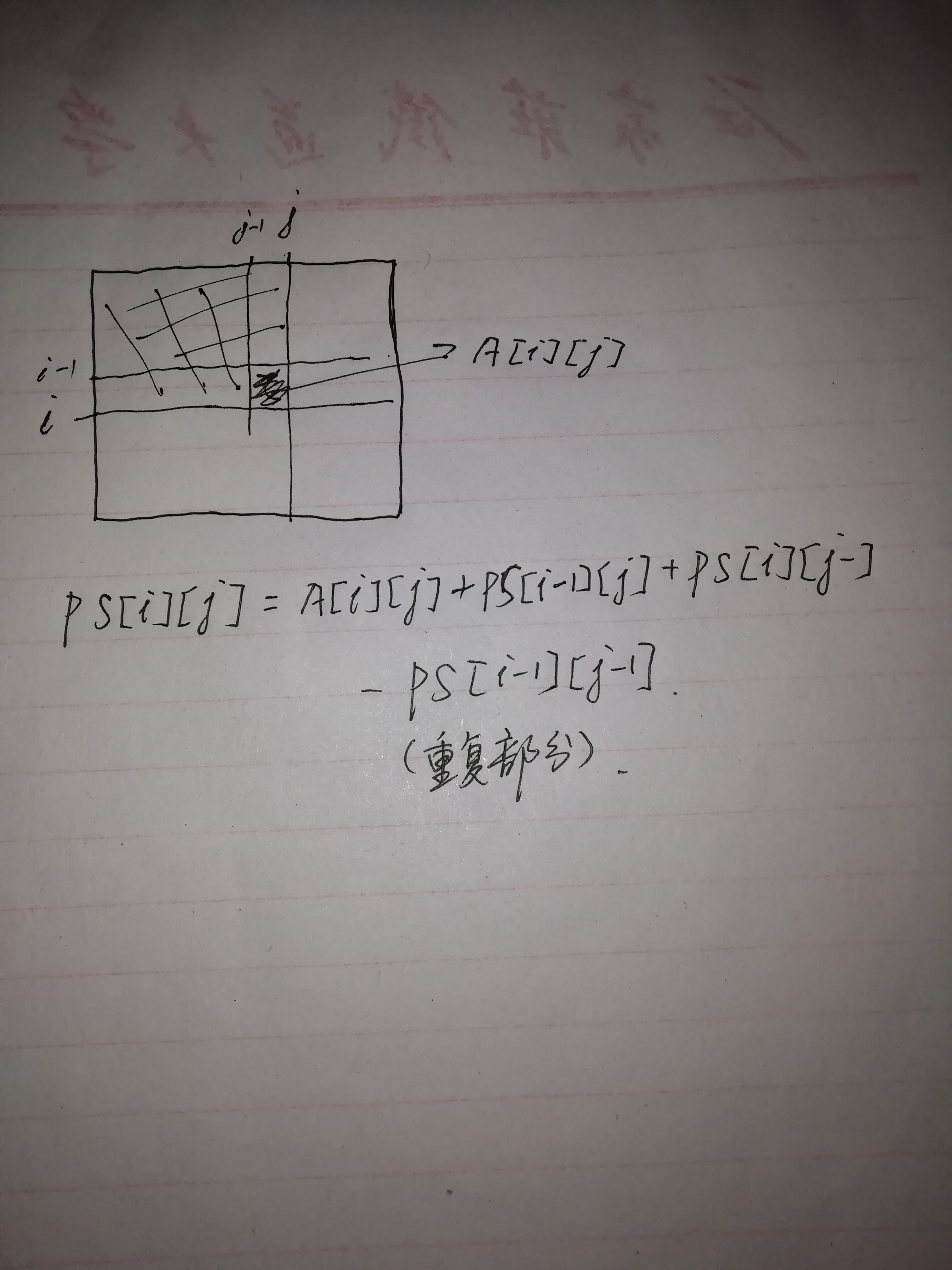  　　通过公式PS[i][j] = A[i][j]+PS[i-1][j]+PS[i][j-1]-PS[i-1][j-1]来求一个矩阵部分和

 

A(0,0)	...	A(0,j)	...	A(o,n)
...	...	...	...	...
A(i,0)	...	A(i,j)	...	A(i,n)
...	...	...	...	...
A(m,0)	...	A(m,j)	...	A(m,n)

　　先固定A(0,0)点，然后一直到A(i,j)做矩阵的部分和，

　　然后再依次分别与之后的做比较，最后得出最大值

 

 

 

 

 

　　

#include <iostream>
using namespace std;
#define M 1000
int A[M][M];
int AS[M][M];
inline int ArraySum(int s,int t,int i,int j)//定义求数组部分和函数
{
    return AS[i][j]-AS[i][t-1]-AS[s-1][j]+AS[s-1][t-1];
}
int max(int a,int b)
{
    return(a>b?a:b);
}
int main()  
{  
    int m,n,i,j;
    cout<<"请输入数组的行:";
    cin>>n;
    cout<<"请输入数组的列:";
    cin>>m;
    cout<<"请输入一个数组:"<<endl;
    for(i=0;i<n;i++)
    {
        for(j=0;j<m;j++)
        {
            cin>>A[i][j];
        }
    }
    // 计算数组的部分和  
    for(i=0;i<n;i++)//以(0,0)为定点一直到(i,j)求部分和
    {
        for(j=0;j<m;j++)
        {
            AS[i][j]=A[i][j]+AS[i-1][j]+AS[i][j-1]-AS[i-1][j-1];
        }
    }
    int Max=A[0][0];
    for(int a=0;a<n;a++)
    {
        for(int c=a;c<n;c++)
        {  
            // 将子数组上下边界设为第a行和第c行，在这些子数组中取最大值  
            int IV=ArraySum(a,0,c,0);
            for(j=1;j<m;j++)
            {  
                IV=max(ArraySum(a,j,c,j),ArraySum(a,j,c,j)+IV);
                Max=max(IV,Max);
            }  
        }
    }
    cout<<"数组最大子数组之和为:"<<Max<<endl;
}

　　　　　　

总结：

　　仔细学习了数组相关知识，思考了如何进行最大子数组的判断，并且与同学相互讨论增加自己的思考范围，然后参考网上大佬的做法，与队友经过长时间分析理解，最后得出这个算法。