Convenient Location(最短路之弗洛伊德)

#include <cstdio> #include <cstring> #include<iostream> #include<queue> #include<stack> #include<cmath> #include <map> #include <algorithm> using namespace std; map<string, string>mp; vector<vector<int> >G; const int INF=0x3f3f3f3f; const int maxn=1100; int maps[maxn][maxn]; int n, m; int main() { while(scanf("%d", &n), n) { m=0; memset(maps, INF, sizeof(maps)); for(int i=0; i<n; i++) { int u, v, w; scanf("%d %d %d", &u, &v, &w); m=max(m, max(u, v)); maps[u][v]=maps[v][u]=w; } for(int k=0; k<=m; k++) { for(int i=0; i<=m; i++) { for(int j=0; j<=m; j++) maps[i][j]=min(maps[i][j], maps[i][k]+maps[k][j]); } } int sum=INF, index; for(int i=0; i<=m; i++) { int ans=0; for(int j=0; j<=m; j++) if(i!=j) ans+=maps[i][j]; if(sum>ans) { sum=ans; index=i; } } printf("%d %d\n", index, sum); } return 0; }
Aizu———0819
这是河南多校大一训练赛的一道签到题,还以为被坑了呢,其实就是很简单
考察了弗洛伊德算法的本质:弗洛伊德算法:每一对顶点之间的最短路径,最终点与点之间的距离都会被更新到最小
不过要注意弗洛伊德算法的时间复杂度O(n3);只能用于点比较少边多的图。
题意就是:找到一个点到其他点和最小,输出此点和最短路径和
Convenient Location
Time Limit : 1 sec, Memory Limit : 65536 KBConvenient Location
来春卒業するAさんは,就職を機に引越しをすることにしました。就職する会社は,オフィスがい くつかの町にあって、日によって出勤するオフィスが違います。そこでAさんは,どこのオフィスに 行くにも時間の短い町に住もうと考えました。
そこであなたは、Aさんを助けるため、住むのに一番便利な町を探すことになりました。
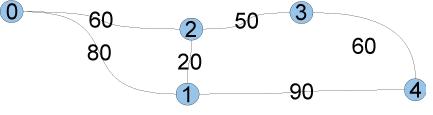
町には0から始まる番号が振られており、町と町の間には道があります。それぞれの道に対して通 勤時間が決まっています。Aさんがある町に住んでいる場合に、自分の町のオフィスまでの通勤時間 は0とします。このときに全ての町までの通勤時間の総和を考えます。例えば,町と道の配置が上の 図のようになっていて、Aさんが町1に住んだ場合には、それぞれの町までの通勤時間は
町0まで 80 町1まで 0 町2まで 20 町3まで 70 町4まで 90
となり、総和は260となります。
道の数と、全ての道の情報を入力とし、それぞれの町に住んだ場合の通勤時間の総和を計算し、そ れが最小となる町の番号と、そのときの通勤時間の総和を出力するプログラムを作成してください。 ただし、通勤時間の総和が最小となる町が複数ある場合は、一番小さい町の番号及びその時の通勤時 間の総和を出力してください。町の総数は10以下、道の総数は45以下とし、全ての道は双方向に移動 でき、通勤時間は方向によって変わらないものとします。また、どの町からでもその他全ての町への 経路があるものとします。
Input
複数のデータセットの並びが入力として与えられます。入力の終わりはゼロひとつの行で示されま す。 各データセットは以下のとおりです。
1行目 道の数n(整数)
2行目 第1の道の情報 a1 b1 c1(それぞれ整数;半角空白区切り)
各記号の意味は以下のとおりです。
a1 b1:この道がつないでいる町の番号
c1:a1、b1間の通勤時間
3行目 第2の道の情報 a2 b2 c2
:
n+1行目 第nの道の情報 an bn cn
Output
入力データセット毎に通勤時間の総和が最小になる町の番号及びその時の通勤時間の総和を出力し ます。(半角空白区切り)
Sample Input
6 0 1 80 1 2 20 0 2 60 2 3 50 3 4 60 1 4 90 2 0 1 1 1 2 1 0
Output for the Sample Input
2 240 1 2





