大话数据结构-图

文章知识点来至于大话数据结构里边章节知识，这篇主要介绍图在计算机中存储形式，以及在某些算法领域中对图的相关应用。本篇涉及到的知识点也比较多在图的遍历中介绍了深度优先遍历、广度优先遍历；在最小生成树节介绍了普利姆算法和克鲁斯卡尔算法；最短路径中介绍了迪杰斯特拉算法、佛洛依德算法；本篇后边还介绍了拓扑排序以及关键路径等知识点。本篇对算法进行了描述和实现，在实现代码的同时添加了流程图。相关代码源码请查看文章最后。本篇最后的算法描述和流程图以及代码实现是重点，如果对本篇感兴趣一定要通过该部分来巩固数据机构。

图

1 图的定义

图是由顶点的有穷非空集合和顶点之间边的集合组成，通过表示为G(V,E)，其中，G标示一个图，V是图G中顶点的集合，E是图G中边的集合。

无边图：若顶点Vi到Vj之间的边没有方向，则称这条边为无项边（Edge），用序偶对(Vi,Vj)标示。

对于下图无向图G1来说，G1=(V1, {E1})，其中顶点集合V1={A,B,C,D}；边集合E1={(A,B),(B,C),(C,D),(D,A),(A,C)}:

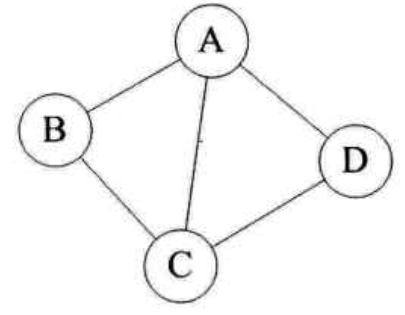
有向图：若从顶点Vi到Vj的边是有方向的，则成这条边为有向边，也称为弧（Arc）。用有序对（Vi，Vj）标示，Vi称为弧尾，Vj称为弧头。如果任意两条边之间都是有向的，则称该图为有向图。

有向图G2中，G2=（V2,{E2}），顶点集合（A,B,C,D）,弧集合E2={<A,D>,{B,A},<C,A>,<B,C>}.

权（Weight）：有些图的边和弧有相关的数，这个数叫做权（Weight）。这些带权的图通常称为网（Network）。

图的定义和术语总结：

2 图的抽象数据类型

基本操作抽象：

1、图的存储结构

邻接矩阵：图的邻接矩阵存储方式是用两个数组来标示图。一个一位数组存储图顶点的信息，一个二维数组（称为邻接矩阵）存储图中边或者弧的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

实例如下，左图是一个无向图。右图是邻接矩阵表示：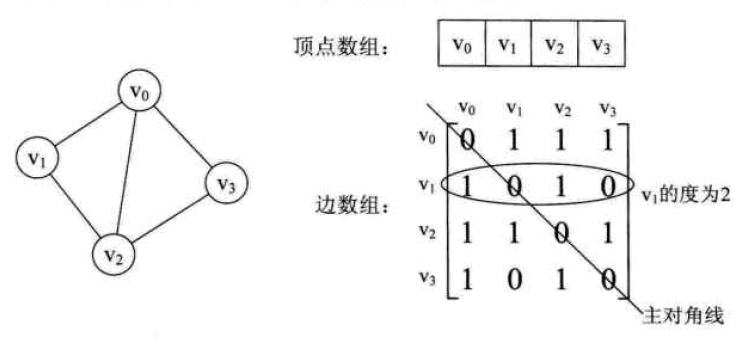

邻接矩阵代码存储结构：

无向网图的创建代码，时间复杂度为O{n + n² + e}。

邻接表

用数组和链表结合的存储方式来标示图的方法称为邻接表。

邻接表处理思路

邻接表存储结构

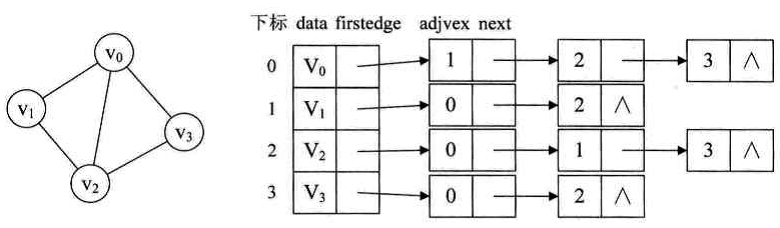
邻接表存储代码结构

邻接表创建代码

十字链表（OrthogonalList）

十字链表把邻接表与逆邻接表结合起来，解决了出度和入度的问题。

3 图的遍历

定义：从图中某个顶点出发访遍图中其余顶点，且使每个顶点仅被访问依次，这一过程叫做图的遍历.

遍历方法：深度优先遍历和广度优先遍历

深度优先遍历

从图中某个顶点出发v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先便利图，知道图中所有和v有相同路径的顶点都被访问。

深度优先遍历采用邻接矩阵遍历：

深度优先遍历采用邻接表遍历：

广度优先遍历

广度优先遍历（Breadth_First_Search）又称为广度优先搜索，简称BFS。

邻接矩阵广度算法实现：

邻接表广度优先算法实现：

4 最小生成树

定义：我们把构造连通图的最小代价生成树称为最小生成树。

最小生成树实现算法：普利姆算法和克鲁斯卡尔算法

鲁斯卡尔算法

定义：

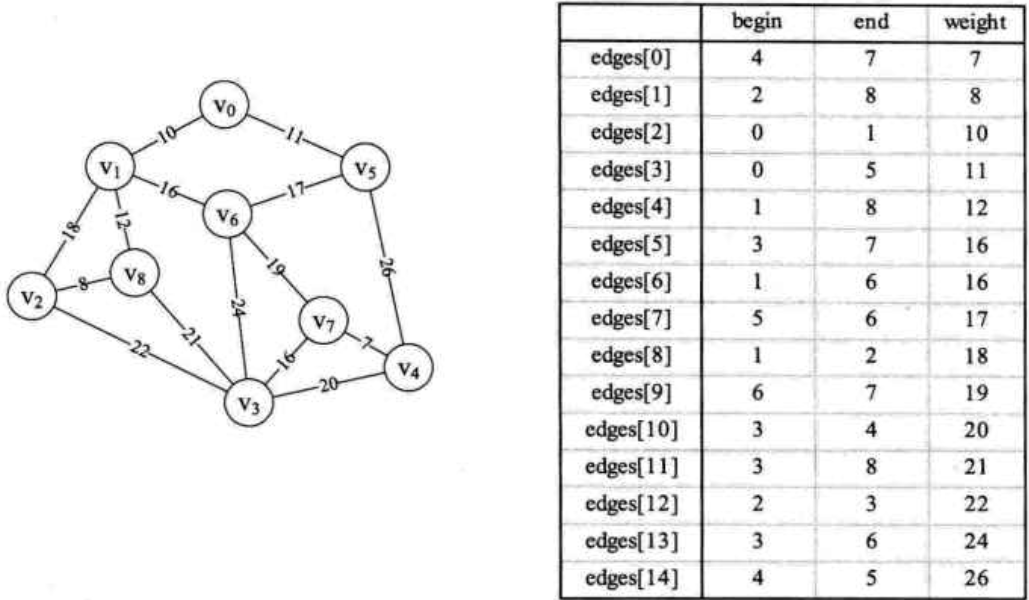
数据初始化：我们将下图的邻接矩阵通过程序转化为右图的边集数组，并且对他们按权值从小到大排序。

算法流程图：

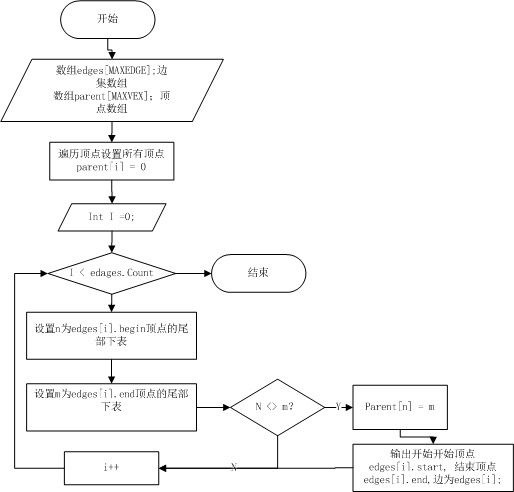
　　　　算法代码实现：

5 最短路径

定义：对于网图来说，最短路径是指两个顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点式源点，最后一个顶点是终点。

两种计算最短路径算法：迪杰斯特拉(Djikstra)算法和佛洛伊德算法

迪杰斯特拉(Djikstra)算法

算法描述：迪杰斯特拉算法并不是一下子求出开始节点到尾节点的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果。

流程图：

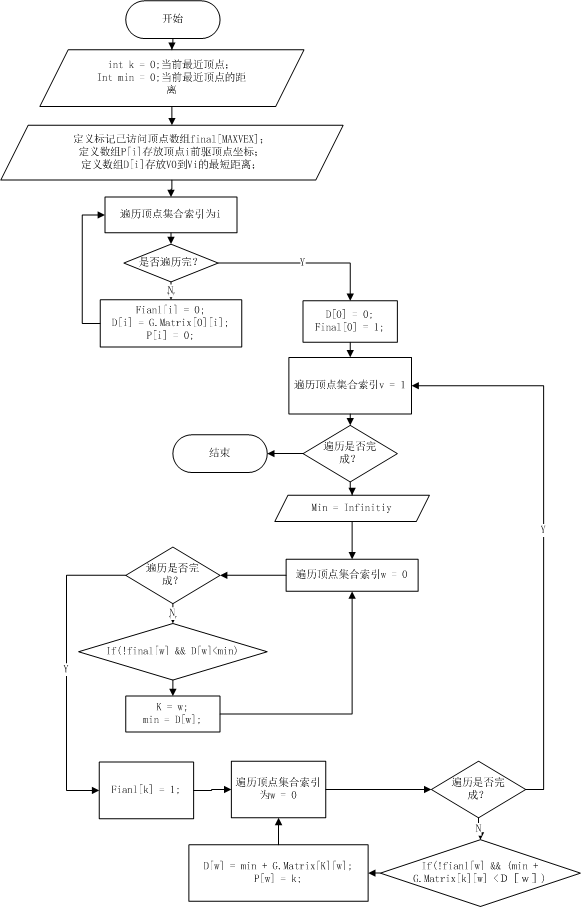
迪杰斯特拉代码实现：

5 拓扑排序

定义

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为AOV网(Activity On Vertex)。

设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列V1,V2…..,Vn满足若从顶点Vi到顶点Vj有一条路径，则在顶点序列中Vi必在Vj顶点之前。则我们称这样的顶点序列为拓扑序列。

所谓拓扑序列，其实就是对一个有向图构造拓扑序列的过程。

数据结构

顶点结构：

参考拓扑图：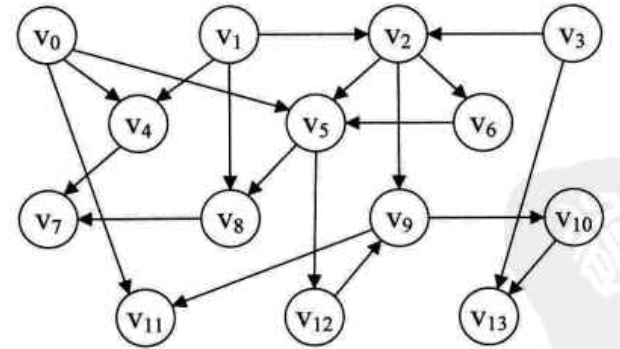

算法实现：

6 关键路径

定义

在一个表示工程的带权有向图中，用顶点表示事件，用有向图表示活动，用边上的权值表示活动的持续事件，这种这种有向图的边表示活动图，我们称之为AOE网(Activity On Edge Network)。

我们把路径上各

个活动所持续的时间之和称为路径的长度，从原点到汇点具有最大长度的路径叫做关键路径，在关键路径上的活动叫关键活动。

7 迪杰斯特拉算法求最短路径（C#版算法实现）：

 public class DjikstraAlgorithm
    {
        public const int INFINITY = 65535;

        public static void CaculateFinalWay(int[][] matrix, int maxVex, out int[] prevMatrix, out int[] weightTable)
        {
            var minWeightKey = 0;
            var finals = new bool[maxVex];

            prevMatrix = new int[maxVex];
            weightTable = new int[maxVex];

            for (var i = 0; i < maxVex; i++)
            {
                finals[i] = false;
                prevMatrix[i] = 0;
                weightTable[i] = matrix[0][i];
            }
            weightTable[0] = 0;
            finals[0] = true;
            for (var v = 1; v < maxVex; v++)
            {
                var minWeightValue = INFINITY;
                for (var w = 0; w < maxVex; w++)
                {
                    if (!finals[w]  && weightTable[w] < minWeightValue)
                    {
                        minWeightKey = w;
                        minWeightValue = weightTable[w];
                    }
                }

                finals[minWeightKey] = true;

                for (var w = 0; w < maxVex; w++)
                {
                    if (!finals[w] && minWeightValue + matrix[minWeightKey][w] < weightTable[w])
                    {
                        weightTable[w] = minWeightValue + matrix[minWeightKey][w];
                        prevMatrix[w] = minWeightKey;
                    }
                }
            }
        }
    }

迪杰斯特拉算法

8 迪杰斯特拉算法单元测试

 1  private static void TestDjikstraAlgorithm()
 2         {
 3             const int max = DjikstraAlgorithm.INFINITY;
 4             var matrix = new int[][]
 5                              {
 6                                  new int[] {  0,  1,   5, max, max, max, max, max, max}, 
 7 
 8                                  new int[] {  1,  0,   3,   7,   5, max, max, max, max},
 9 
10                                  new int[] {  5,  3,   0, max,   1,   7, max, max, max},
11 
12                                  new int[] {max,  7, max,   0,   2, max,   3, max, max},
13 
14                                  new int[] {max,  5,   1,   2,   0,   3,   6,   9, max},
15 
16                                  new int[] {max, max,  7, max,   3,   0, max,   5, max},
17 
18                                  new int[] {max, max, max,  3,   6, max,   0,   2,   7},
19 
20                                  new int[] {max, max, max,max,   9,   5,   2,   0,   4},
21 
22                                  new int[] {max, max, max,max, max, max,   7,   4,   0}
23                              };
24 
25             int[] preMatrix;
26             int[] weightTable;
27             DjikstraAlgorithm.CaculateFinalWay(matrix, 9, out preMatrix, out weightTable);
28             //验证V8的权值
29             Assert.IsEqual(weightTable[8], 16);
30             //验证V0到V8的最短路径
31             Assert.IsEqual("V0->V1->V2->V4->V3->V6->V7->V8", GetFinalWay(preMatrix));
32         }
33 
34         private static string GetFinalWay(int[] preMatrix)
35         {
36             var index = 8;
37             var finalWay = "V" + index;
38 
39             while (index != 0)
40             {
41                 finalWay = string.Format("V{0}->", preMatrix[index]) + finalWay;
42                 index = preMatrix[index];
43             }
44 
45             return finalWay;
46         }

迪杰斯特拉算法单元测试

最后附上源代码下载地址：

http://download.csdn.net/detail/w_wanglei/5689883

posted @ 2013-07-13 11:01 heavi 阅读(14619) 评论(1) 编辑收藏举报

刷新页面返回顶部

Heavi的博客

无善无恶心之体，有善有恶意之动；知善知恶是良知，为善去恶是格物。

大话数据结构-图

图

公告