YbtOJ20030 连珠风暴

WARNING:长文警告

链接

戳这里

题目

题目描述

给定\(M\)种颜色的珠子，每种颜色珠子的个数均不限，将这些珠子做成长度为\(N\)的项链。

问能做成多少种不重复的项链。

两条项链相同，当且仅当两条项链通过旋转或是翻转后能重合在一起，且对应珠子的颜色相同。

输入格式

从文件necklace.in中读入数据。

一行两个整数分别表示\(M,N\)。

输出格式

输出到文件necklace.out中。

一行一个整数表示答案。

DFS解法

这个解法来源于机房数论大佬梦神

这是他的代码

#include<iostream>
#include<map>
#include<cstdio>
#include<ctime>
#include<cstdlib>

using namespace std;
int n,m,ans;
long long cnt;

map <string,bool>have;

string l[100] ,p;

inline void dfs(string s){
	string r="";
	string l[100];
	for(int i=0;i<=n;i++){
		l[i]="";
	}
	for(int i=1;i<=n;i++){
		r+=s[n-i];
	}
	l[n]=r;
	for(int is=0;is<n;is++){
		string x="";
		for(int j=is;j<n;j++){
			x+=s[j];
		}
		for(int j=0;j<is;j++){
			x+=s[j];
		}
		l[is]=x;
	}
	for(int is=0;is<=n;is++){
		if(have[l[is]]){
			return;
		}
	}
	ans++;
	for(int i=0;i<=n;i++){
		have[l[i]]=1;
	}
	p=s;
	for(int i=2;i<=m;i++){
		for(int j=0;j<n;j++){
			int kk=p[j];
			p[j]=i+'0';
			dfs(p);
			p[j]=kk;
		}
	}
}

int main()
{
	cin>>m>>n;
	string nmzl="";
	for(int i=1;i<=n;i++){
		nmzl+='1';
	}
	dfs(nmzl);
	cout<<ans;
	return 0;
}

\(P\acute{o}lya\)定理解法

\(P\acute{o}lya\)定理

首先，在讲这个复杂的定理前，我们先讲一些前置芝士

大型定理的铺垫——前置芝士

前置芝士

  • 群
  • 置换
  • 置换群
  • 群作用
  • 轨道-稳定子定理

群

群是什么呢？正规解释是这样的：

定义集合\(G\)和作用与集合\(G\)的二元运算\(\times\)

若其满足以下\(4\)个性质，则称其为一个群\((Group)\)，记为 \((G,\times)\)

  1. 封闭性\((Closure)\)

    若存在\(a\)和\(b\)满足\(a\in G,b\in G\)，则有\(a\times b\in G\);

  2. 结合律\((Associativity)\)

    对于任意\(a,b,c\)有\((a\times b)\times c = a\times (b\times c)\)

  3. 单位元\((Identity)\)

    存在\(e\in G\)，满足对于任意\(a\in G\)有：\(a\times e = e\times a\)

    这样的\(e\)被称为单位元。单位元唯一

  4. 逆元\((Inverse)\)

    对于任意\(a\in G\)存在\(a'\in G\) 满足\(a\times a' = a'\times a = e\)，\(a'\)唯一。

可以简要理解为一个比较高级的集合

置换

对于置换，我们通常用双行表示法表示。

例如：

\[\sigma = \left( \begin{matrix} 1 & 2 & 3 & 4 & 5 & 6\\ 6 & 3 & 4 & 5 & 1 & 2 \end{matrix} \right)\]

相当于把第一行的元素替换为第二行的元素，写作\(\sigma(a)\)

置换群

简单地说，一个群多种置换组成的群，就是置换群

它同群一样，有封闭性、结合律、单位元、逆元

群作用

对于一个集合\(M\)和一个群\(G\)

如果二元函数\(\varphi(v,k)\)，\(v\)为群中的元素，\(k\)为集合中的元素，且有：

\[\varphi(e,k) = k (e为单位元) \]

\[\varphi(g,\varphi(s,k)) = \varphi(g \times s,k) \]

就称群\(G\)作用与集合\(M\)

轨道-稳定子定理

轨道

一个作用在\(X\)上的群\(G\)，\(X\)中的一个元素\(x\)的轨道为\(x\)通过\(G\)中的元素可以转移到的元素的集合。

可以形象地理解为一个火车所走的元素形成的集合。

\(x\)的轨道被记为\(G(x)\)，我们可以用\(g(x)\)表示群\(G\)元素\(g\)所用于\(x\)的群作用的返回值，即

\[g(x) = \varphi(g,x) \]

稳定子

先上定义：

\[G^x=\{g|g\in G,g(x)=x\} \]

简要地用语言描述一下，就是群\(G\)中满足\(g(x)=x\)的所有元素\(g\)所构成的集合

轨道-稳定子定理

先上公式：

\[|G^x|\times|G(x)|=|G| \]

证明略微繁琐，感兴趣的同学可以自己搜一下

轨道-稳定子定理证明

预备工作完成——正片开始

\(Burnside\)引理

\[|X/G|=\frac{1}{|G|}\sum_{|G|}|X^g| \]

\(|X/G|\)为\(X\)关于\(G\)的轨道数

其中\(X^g=\{x|g(x)=x,x\in X\}\)，我们称\(X^g\)是\(X\)在置换\(g\)下的不动点集合。

什么是不动点？就是经过置换后仍然不动的点。

举例：对于置换群\(\sigma = \left( \begin{matrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{matrix} \right)\)，显然\(3\)就是不动点

文字描述：\(X\)关于置换群\(G\)的轨道数，等于\(G\)中每个置换下不动点的个数的平均数。

证明较繁琐，故此略去

Burnside引理证明

终极结论—\(P\acute{o}lya\)定理

\(P\acute{o}lya\)定理

\(P\acute{o}lya\)定理其实是\(Burnside\)引理的一种特殊形式。

\(Burnside\)引理已经给出了等价类个数的表达式，\(Polya\)定理进一步具体到染色问题上，给出了本质不同的染色方案数的表达式。

在使用\(Burnside\)解决染色问题的时候，我们需要求的是不动点的数量，而对于上述的置换，假设我们令每个\(i\)向\(a_i\)连一条边容易发现会得到若干个环，仔细思考，每个环的颜色应当相同。

令\(c(g)\)为置换\(g\)所包含的循环个数

将这个等式代入Burnside引理中，得到总的染色方案数为

\[\frac{1}{|G|}\sum_{g\in G}m^{c(g)} \]

这就是\(P\acute{o}lya\)定理！

苦难后的幸福——进入问题

切入问题

那我们考虑一下这道题，是一个明显的\(P\acute{o}lya\)计数问题。它重叠的方案有几种呢？显然，两种——旋转和翻转

旋转

将环顺时针旋转\(i\)格后，循环节个数为\(gcd(n,i)\)，利用\(P\acute{o}lya\)定理，显然染色方案为\(\Sigma c^{gcd(n,i)}\)

翻转

这里得考虑两种情况，奇数与偶数

  • 奇数

    当\(n\)为奇数时，共有\(n\)个循环节个数为\((n/2+1)\)的循环群，染色方案为\(n*c^(n/2+1)\)

    那为什么循环群的个数为\((n/2+1)\)呢？诸位可以自己举例理解一下。

  • 偶数

    当\(n\)为偶数时，共有\(n\)个循环群，其中有\(n/2\)个的循环节个数为\(（n/2 +1)\)， 有\(n/2\)个的循环节个数为\((n/2)\)。

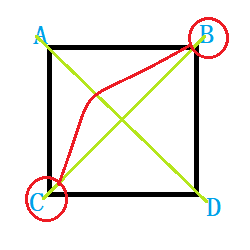
    拿正方形为例，四个顶点编号\(A,B,C,D\).

  • 当以对角的两个顶点连线为对称轴时,这样对称轴有2个\((n/2)\)，经过翻转，\(C,B\)重合，\(A,A\)重合，\(D,D\)重合，那么循环节的个数为\(3\), 即\((n/2+1)\)。染色方案为 \((n/2)*c^{(n/2+1)}\)

四边1

  • 当以两条相对平行的边的中点连线所在直线为对称轴时，这样的对称轴也有两个\((n/2)\)，经过翻转，\(A,B\)重合，\(C,D\)重合，循环节的个数为2，即\((n/2)\)染色方案为\((n/2)*c^{(n/2)}\)

四边2

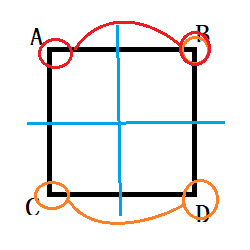
最终累加所有方案得到ans，再除以置换群的个数\(2*n\)，即 \(ans/(2*n)\)为最后答案。

\(Code\)

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

#define LL long long

LL m, n, x, y, ans;

LL gcd(LL a, LL b)  //辗转相除
{
    return b == 0 ? a : gcd(b, a % b);
}

LL power(LL p, LL n)  //幂运算
{
    LL ans = 1;
    while (n--) ans *= p;
    return ans;
}

int main() {
    scanf("%lld%lld", &m, &n);
    for (LL i = 1; i <= n; i++)  //旋转
    {
        ans += power(m, gcd(n, i));
    }
    if (n % 2 == 1)  //翻转奇数
    {
        ans += (n * power(m, n / 2 + 1));
    } else  //翻转偶数
    {
        ans += ((n / 2 * power(m, n / 2 + 1)) + (n / 2 * power(m, n / 2)));
    }
    ans = ans / (2 * n);
    printf("%lld", ans);
    return 0;
}

然后你就可以以十个测试点\(60ms\)的极速\(A\)掉这题了

最终结果

\(The\ End\)

说句闲话，这道题题解给的正解是暴搜。

参考资料：

题解 P4980 【【模板】Polya定理】

【学习笔记】Burnside引理和Polya定理

Polya定理

posted @ 2020-12-12 22:51  W-RB  阅读(182)  评论(0)  编辑  收藏  举报