图论学习笔记

Dijkstra单源最短路径

堆优化。注意要定义成小根堆，而priority_queue默认大根堆

再就是每个点最多入队一次，可以用vis数组记录

证明：如果已经出队，说明队列中全都是val值比他大的(负权边?)，这样他的val值一定已经是最终值了；

如果没有入队，进行更改之后会在堆中体现，不需要担心之后还会更新他的val值

#include<bits/stdc++.h>
using namespace std;

const int N=200000,M=1000000,inf=(1<<30)-1+(1<<30);
int n,m,s,cnt;
struct node{
    int num,head,val=inf,vis=0;
    bool operator <(const node &tmp)const{
        return val>tmp.val;//change it into a small root heap
    }
}a[N];
struct edge{
    int nxt,to,len;
}e[M];
priority_queue<node>q;

void add(int u,int v,int w){
    e[++cnt].nxt=a[u].head;
    e[cnt].to=v;
    e[cnt].len=w;
    a[u].head=cnt;
}

void Dij(){
    a[s].val=0;q.push(a[s]);
    while(!q.empty()){
        node x=q.top();q.pop();
        if(a[x.num].vis) continue; a[x.num].vis=1;
        //When it comes to here,x.val is the newest value.It's useless to update once again.
        for(int i=x.head;i;i=e[i].nxt){
            if(e[i].len+x.val<a[e[i].to].val){
                a[e[i].to].val=e[i].len+x.val;
                q.push(a[e[i].to]);
            }
        }
    }
}

int main(){
    cin>>n>>m>>s;
    for(int i=1;i<=n;++i) a[i].num=i;
    for(int i=1;i<=m;++i){int u,v,w;cin>>u>>v>>w;add(u,v,w);}
    Dij();
    for(int i=1;i<=n;++i) cout<<a[i].val<<' '; cout<<endl;
    return 0;
}

SPFA找负环

vis记录目前已经在队列中的不再次入队，稠密图中效率不如floyd

多测清空！[怒]

#include<bits/stdc++.h>
using namespace std;

const int N=10000,inf=1000000000;
int n,m;
struct node{
	int val,cnt,head,vis;
}nd[N];
queue<int> q;
struct edge{
	int nxt,len,to;
}e[N];int cnt;

void memst(){//多测清空！！！
	cnt=0;nd[0].val=inf;
	while(!q.empty()) q.pop();
	for(int i=1;i<=n;++i) nd[i]=nd[0];
	for(int j=1;j<=m;++j) e[j]=e[0];
}

void add(int u,int v,int w){
	e[++cnt].to=v;
	e[cnt].len=w;
	e[cnt].nxt=nd[u].head;
	nd[u].head=cnt;
}

int spfa(){
 	++nd[1].cnt;nd[1].val=0; q.push(1);
	while(!q.empty()){
		int x=q.front();q.pop();nd[x].vis=0;
		for(int i=nd[x].head;i;i=e[i].nxt){
			int v=e[i].to;
			if(nd[v].val>nd[x].val+e[i].len){
				nd[v].val=nd[x].val+e[i].len;
				if(nd[v].vis) continue;
				++nd[v].cnt;nd[v].vis=1;//这里注意记录入队次数而不是松弛次数，以防止重边导致松弛次数增加引起的误判。
				if(nd[v].cnt>=n) return 1;
				q.push(v);
			}
		}
	}
	return 0;
}

int main(){
	int T;cin>>T;while(T--){
		cin>>n>>m;memst();
		for(int i=1;i<=m;++i){
			int u,v,w;cin>>u>>v>>w;add(u,v,w);
			if(w>=0) add(v,u,w);
		}
		if(spfa()) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
	return 0;
}

差分约束方程

学习链接

#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>

#define ll long long
using namespace std;

const int N=20000;//一开始数组还开小了
int n,m;
struct node{
	int dis=1000000000,cnt,head,vis;
}nd[N];
struct edge{
	int nxt,to,len;
}e[N];int cnt;
queue<int> q;

void add(int u,int v,int w){
	e[++cnt].to=v;e[cnt].len=w;
	e[cnt].nxt=nd[u].head;nd[u].head=cnt;
}

int spfa(){
	q.push(0);nd[0].dis=0;nd[0].cnt++;
	while(!q.empty()){
		int u=q.front();q.pop();nd[u].vis=0;
		for(int i=nd[u].head;i;i=e[i].nxt){
			if(nd[u].dis+e[i].len<nd[e[i].to].dis){
				nd[e[i].to].dis=nd[u].dis+e[i].len;
				if(nd[e[i].to].vis) continue;
				nd[e[i].to].vis=1;++nd[e[i].to].cnt;q.push(e[i].to);
				if(nd[e[i].to].cnt==n+1) return 0;
			}
		}
	}
	return 1;
}

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;++i){
		int u,v,w;cin>>u>>v>>w;add(v,u,w);
	}for(int i=1;i<=n;++i) add(0,i,0);
	if(spfa()) for(int i=1;i<=n;++i) cout<<nd[i].dis<<' ';
	else cout<<"NO";cout<<endl;
	return 0;
}

[NOIPpj2017]棋盘

死去的回忆开始攻击我，初一的时候因为这道题痛失pj省一（悲）

很巧妙的建图，对周围两层12个点建立无向图跑Dijkstra，复杂度\(O(mlogm)\)，这种做法比用周围一层4个点建图要强，少考虑很多细节

偷一张图（

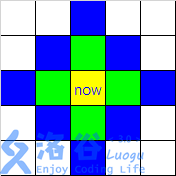
最后别忘了\((m,m),(m-1,m),(m,m-1)\)都可以作为终点

#include<bits/stdc++.h>
using namespace std;

const int inf=1000000000;
int m,n,a[200][200],a1[2000],a2[20000],a3[2000];
struct node{
	int head,dis=inf,num,vis;
	bool operator <(const node &tmp)const{return dis>tmp.dis;}
}nd[20000];int cnt1;
priority_queue<node> q;
struct edge{
	int nxt,to,len;
}e[20000];int cnt2;

void add1(int u,int v,int w){
	e[++cnt2].to=v;e[cnt2].len=w;
	e[cnt2].nxt=nd[u].head;nd[u].head=cnt2;
}

void add(int x,int y,int z){
	int u=(x-1)*m+y-1;
	int _x[12]={-2,-1,-1,-1,0,0,0,0,1,1,1,2};
	int _y[12]={0,-1,0,1,-2,-1,1,2,1,0,-1,0};
	int _k[12]={2,2,0,2,2,0,0,2,2,0,2,2};
	for(int i=0;i<12;++i){
		int __x=x+_x[i],__y=y+_y[i],v=(__x-1)*m+__y-1;
		if(__x>0&&__x<=m&&__y>0&&__y<=m&&a[__x][__y]!=-1)
			if(a[x][y]==a[__x][__y]) {add1(u,v,_k[i]);add1(v,u,_k[i]);}
			else {add1(u,v,_k[i]+1);add1(v,u,_k[i]+1);}
	}
}

void Dij(){
	nd[0].dis=0;nd[0].num=0;q.push(nd[0]);
	while(!q.empty()){
		node x=q.top();q.pop();int u=x.num;nd[u].vis=0;
		for(int i=nd[u].head;i;i=e[i].nxt){
			int v=e[i].to,w=e[i].len;
			if(nd[v].dis>nd[u].dis+w){
				nd[v].dis=nd[u].dis+w;
				if(!nd[v].vis){
					nd[v].vis=1;nd[v].num=v;q.push(nd[v]);
				}
			}
		}
	}
}

int main(){
	cin>>m>>n;
	for(int i=1;i<=m;++i) for(int j=1;j<=m;++j) a[i][j]=-1;
	for(int i=1;i<=n;++i){cin>>a1[i]>>a2[i]>>a3[i];a[a1[i]][a2[i]]=a3[i];}
	for(int i=1;i<=n;++i) add(a1[i],a2[i],a3[i]);
	Dij();
	if(nd[(m-1)*m+m-1].dis==inf&&nd[(m-1)*m+m-2].dis==inf&&nd[(m-2)*m+m-1].dis==inf) cout<<"-1\n";
	else cout<<min(nd[(m-1)*m+m-1].dis,min(nd[(m-1)*m+m-2].dis,nd[(m-2)*m+m-1].dis)+2)<<endl;
	return 0;
}